2 Análise de sobrevivência

---

Análise de sobrevivência, também denominada análise de sobrevida, é um ramo da estatística que estuda o tempo de duração esperado até a ocorrência de um ou mais eventos, tais como morte em organismos biológicos ou falha em sistemas mecânicos. Na agronomia, tem sido bastante utilizada na avaliação residual de produtos fitossanitários em insetos, tempo até a morte em função de um doença, etc.

---

---

2.1 Conjunto de dados

---

O conjunto de dados é de um experimento cujo objetivo é avaliar a mortalidade de insetos em função de alguns produtos comerciais.

tempo=c(10,10,10,10,10,10,10,24,24,24,24,48,10,10,10,10,10,10,10,10,10,10,10,10,24,24,48,48,72,72,72,72,72,72,72,72,10,10,24,24,72,72,72,72,72,72,96,96,10,10,10,48,96,96,144,144,168,168,168,168,10,10,24,24,72,72,72,96,96,120,168,168,10,10,10,10,10,10,10,24,24,24,24,48,10,10,10,24,24,120,120,144,144,144,144,144,10,10,144,144,168,168,168,168,168,168,168,168,24,72,96,96,120,144,168,168,168,168,168,168,24,72,96,120,144,168,168,168,168,168,168,168,10,10,10,10,10,10,24,72,96,168,168,168)
# criando vetor de status (Ocorreu ou nao o evento)
status=c(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,1,1,1,0,0,0,1,0,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1,1,1,1,1,1,1,0,0)
trat=rep(c("T1","T2",'T3'),e=48)
dados=data.frame(trat,tempo,status)

2.2 Histograma

hist(tempo)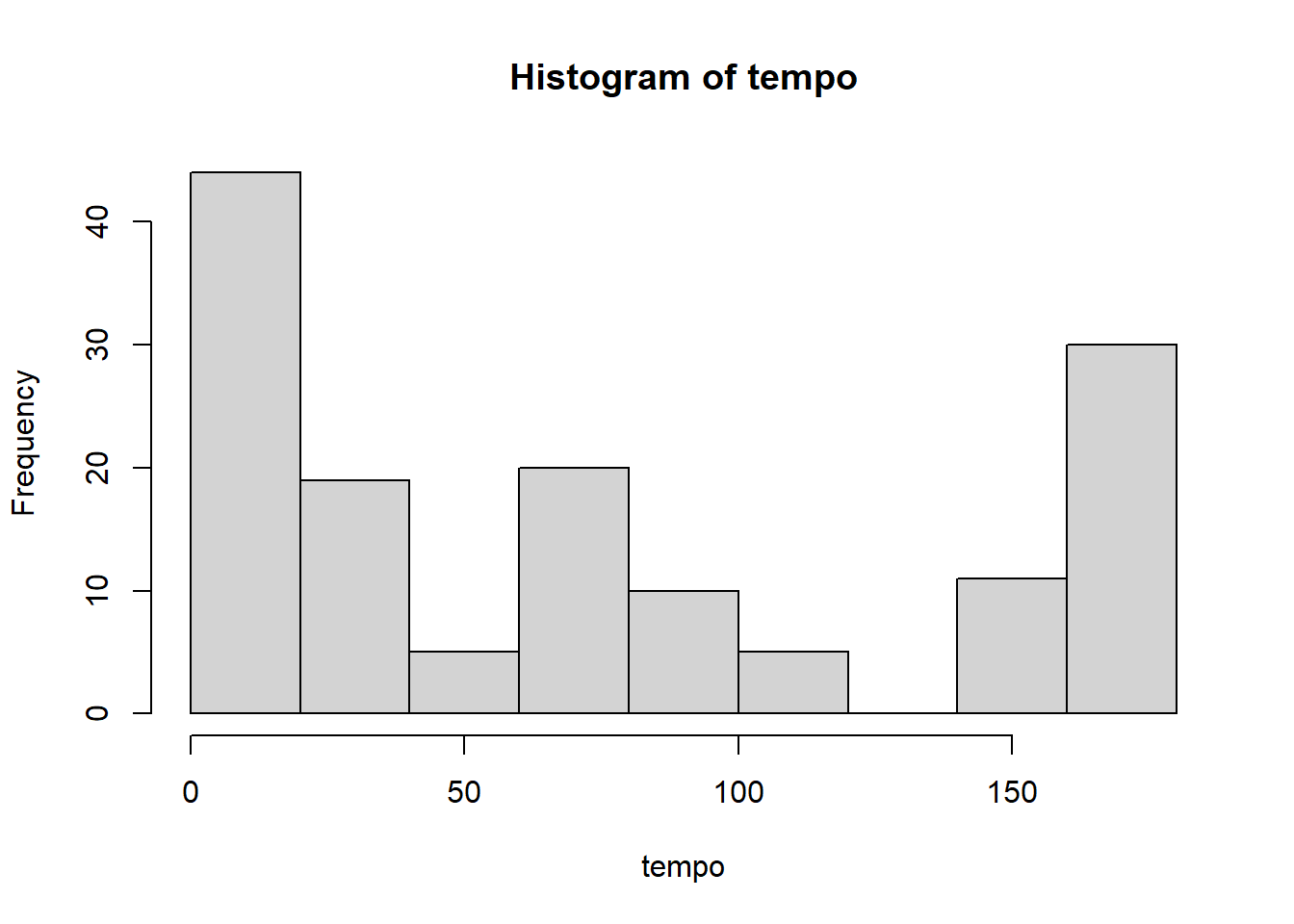

---

2.3 Método não-paramétrico de Kaplan-meier

---

2.3.1 Sem considerar tratamentos

Somente uma análise exploratória geral

library(survival)
library(survminer)
KM <- survfit(Surv(tempo,status) ~ 1, type="kaplan-meier")
summary(KM)

## Call: survfit(formula = Surv(tempo, status) ~ 1, type = "kaplan-meier")
## 
##  time n.risk n.event survival std.err lower 95% CI upper 95% CI
##    10    144      44    0.694  0.0384       0.6231        0.774
##    24    100      19    0.562  0.0413       0.4870        0.650
##    48     81       5    0.528  0.0416       0.4522        0.616
##    72     76      20    0.389  0.0406       0.3169        0.477
##    96     56      10    0.319  0.0389       0.2517        0.405
##   120     46       5    0.285  0.0376       0.2198        0.369
##   144     41      11    0.208  0.0338       0.1515        0.286
##   168     30      12    0.125  0.0276       0.0811        0.193

ggsurvplot(
  fit = survfit(Surv(tempo, status) ~ 1),data=dados, 
  xlab = "Time (hours)", 
  ylab = "Overall survival probability")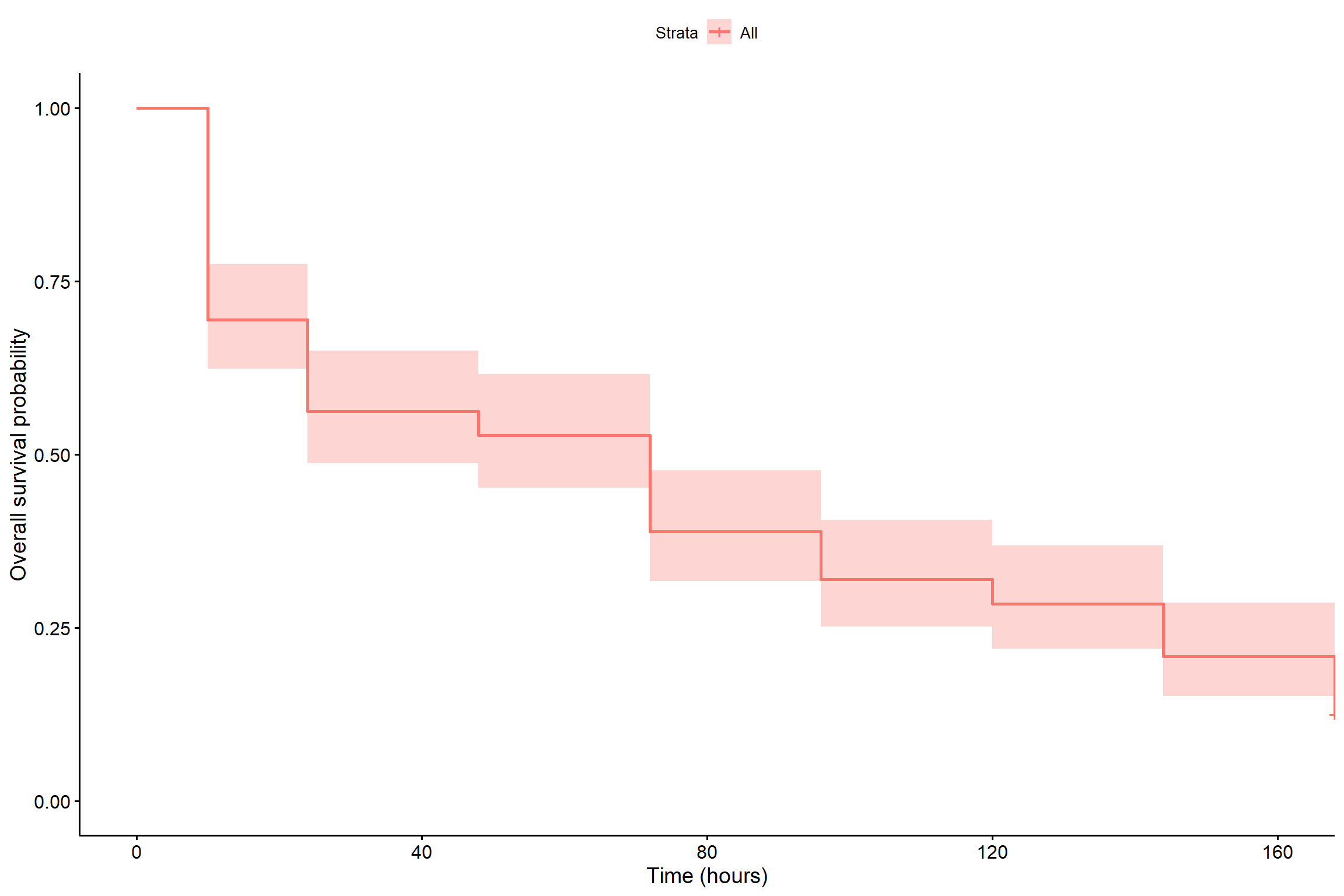

2.3.2 Tempo médio de sobrevivência

a=survival:::survmean(KM, rmean=48)
a$matrix[5]

##   *rmean 
## 33.22222

2.3.3 Considerando tratamentos

2.3.4 Conferindo diferenças par a par

pvalor=pairwise_survdiff(Surv(tempo,status)~trat,data=dados, rho=0)
knitr::kable(pvalor$p.value)

	T1	T2
T2	0.0003111
T3	0.0000000	0.0006521

Todos diferem entre si

2.3.5 Grafico por tratamento usando o método de Kaplan-Meier

KM1 <- survfit(Surv(tempo,status) ~ trat, type="kaplan-meier")
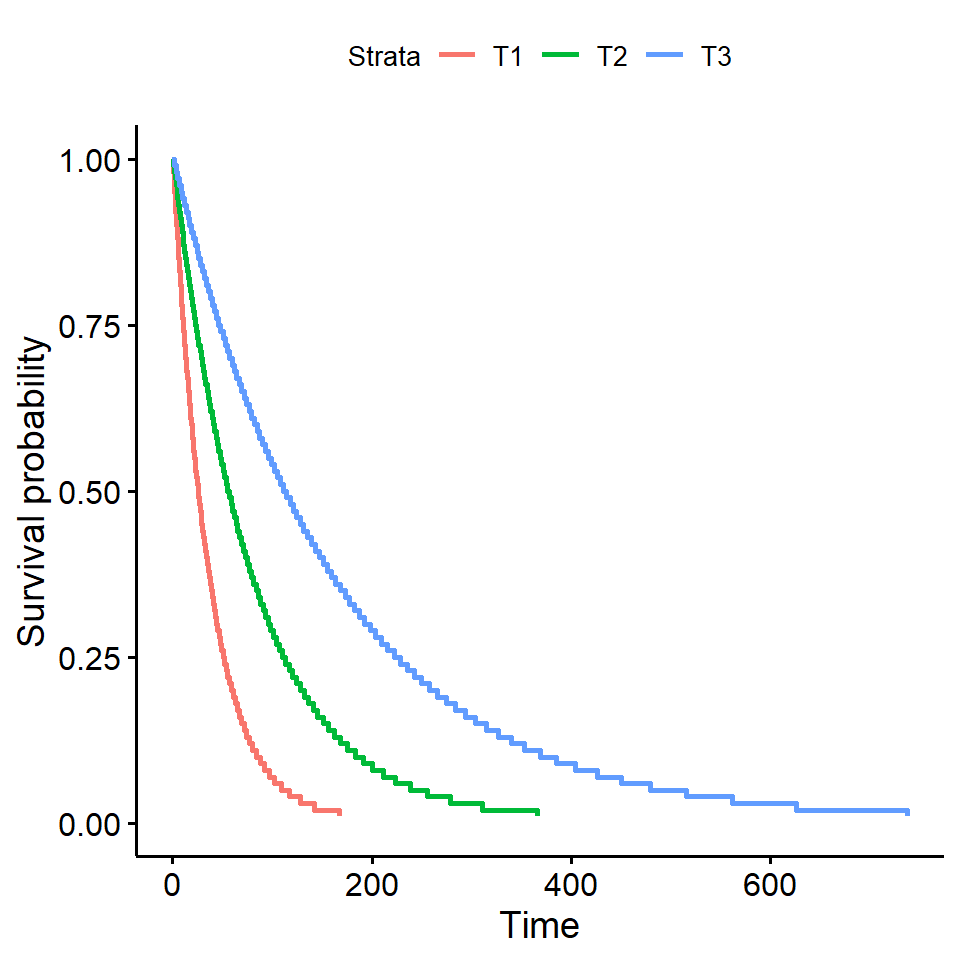
ggsurvplot(
  fit = survfit(Surv(tempo, status) ~ trat),data=dados, 
  xlab = "Time (hours)", 
  ylab = "Overall survival probability")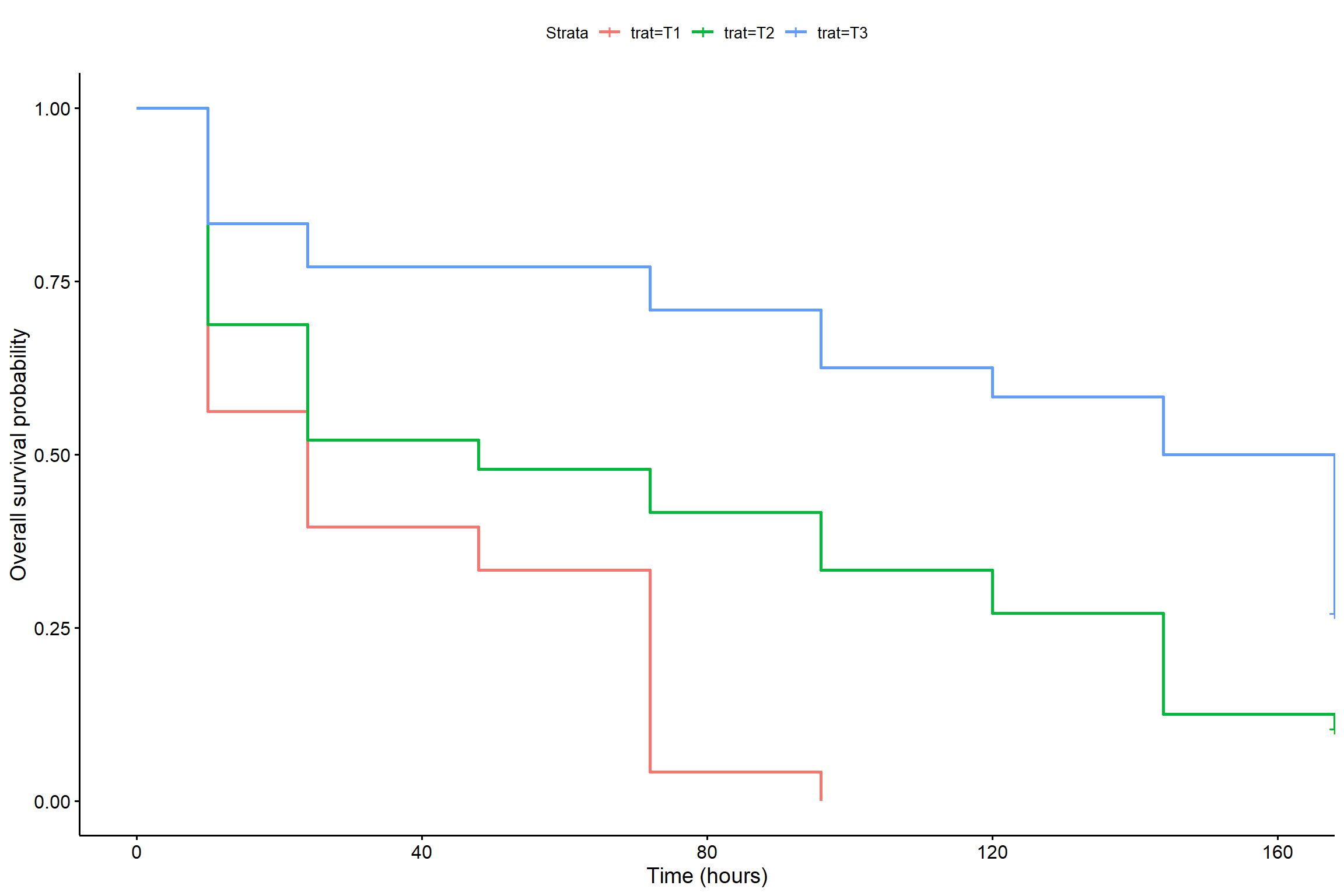

2.3.6 Tempo médio de sobrevivência

survival:::survmean(KM1, rmean=48)$matrix[,5]

##  trat=T1  trat=T2  trat=T3 
## 27.37500 32.12500 40.16667

---

2.4 Modelo paramétrico

---

---

2.4.1 Distribuição exponencial

---

2.4.2 Sem considerar tratamentos

KM <- survreg(Surv(tempo,status) ~ 1, dist="exponential")
summary(KM)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ 1, dist = "exponential")
##              Value Std. Error    z      p
## (Intercept) 4.4473     0.0891 49.9 <2e-16
## 
## Scale fixed at 1 
## 
## Exponential distribution
## Loglik(model)= -686.4   Loglik(intercept only)= -686.4
## Number of Newton-Raphson Iterations: 4 
## n= 144

s <- seq(.01, .99, by = .01)
t_0 <- predict(KM, newdata = data.frame(trat=paste("T1","T2","T3")), 
                 type = "quantile", p = s)
smod <- data.frame(time = c(t_0), # acrescentar os tratamentos 
                   surv = rep(1 - s, times = 1), # mudar o times
                   upper = NA, lower = NA)
ggsurvplot(smod)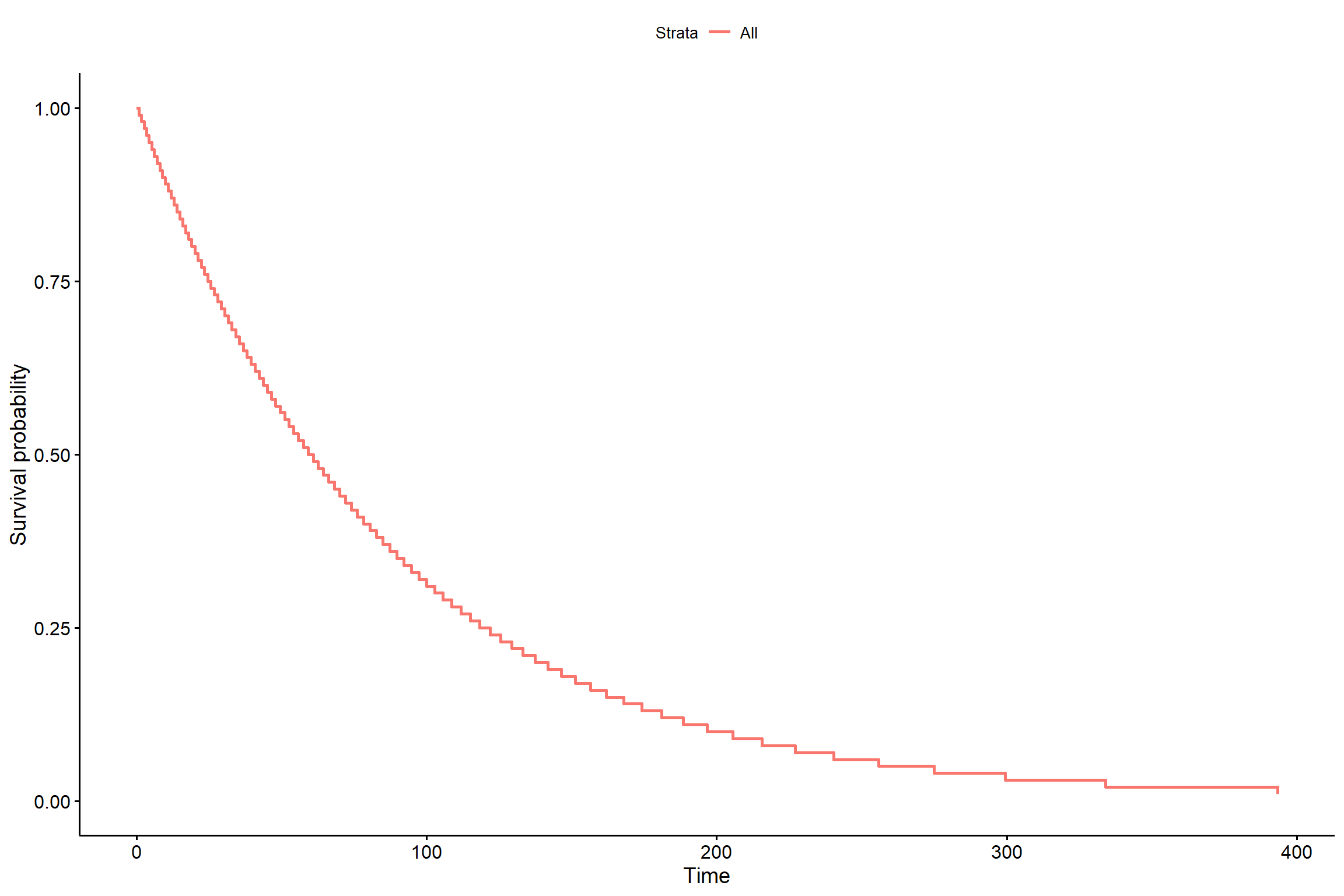  

2.4.3 Considerando tratamentos

library(survival)
library(survminer)
KM2 <- survreg(Surv(tempo,status) ~ trat, dist="exponential")
summary(KM)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ 1, dist = "exponential")
##              Value Std. Error    z      p
## (Intercept) 4.4473     0.0891 49.9 <2e-16
## 
## Scale fixed at 1 
## 
## Exponential distribution
## Loglik(model)= -686.4   Loglik(intercept only)= -686.4
## Number of Newton-Raphson Iterations: 4 
## n= 144

anova(KM2)

##      Df Deviance Resid. Df    -2*LL     Pr(>Chi)
## NULL NA       NA       143 1372.722           NA
## trat  2 44.24522       141 1328.477 2.467593e-10

s <- seq(.01, .99, by = .01)
t_0 <- predict(KM2, newdata = data.frame(trat = "T1"), type = "quantile", p = s)
t_1 <- predict(KM2, newdata = data.frame(trat = "T2"), type = "quantile", p = s)
t_2 <- predict(KM2, newdata = data.frame(trat = "T3"), type = "quantile", p = s)
smod <- data.frame(time = c(t_0, t_1, t_2), # acrescentar os tratamentos 
                   surv = rep(1 - s, times = 3), # mudar o times
                   strata = rep(c("T1", "T2", "T3"), each = length(s)),
                   upper = NA, lower = NA)
ggsurvplot(smod)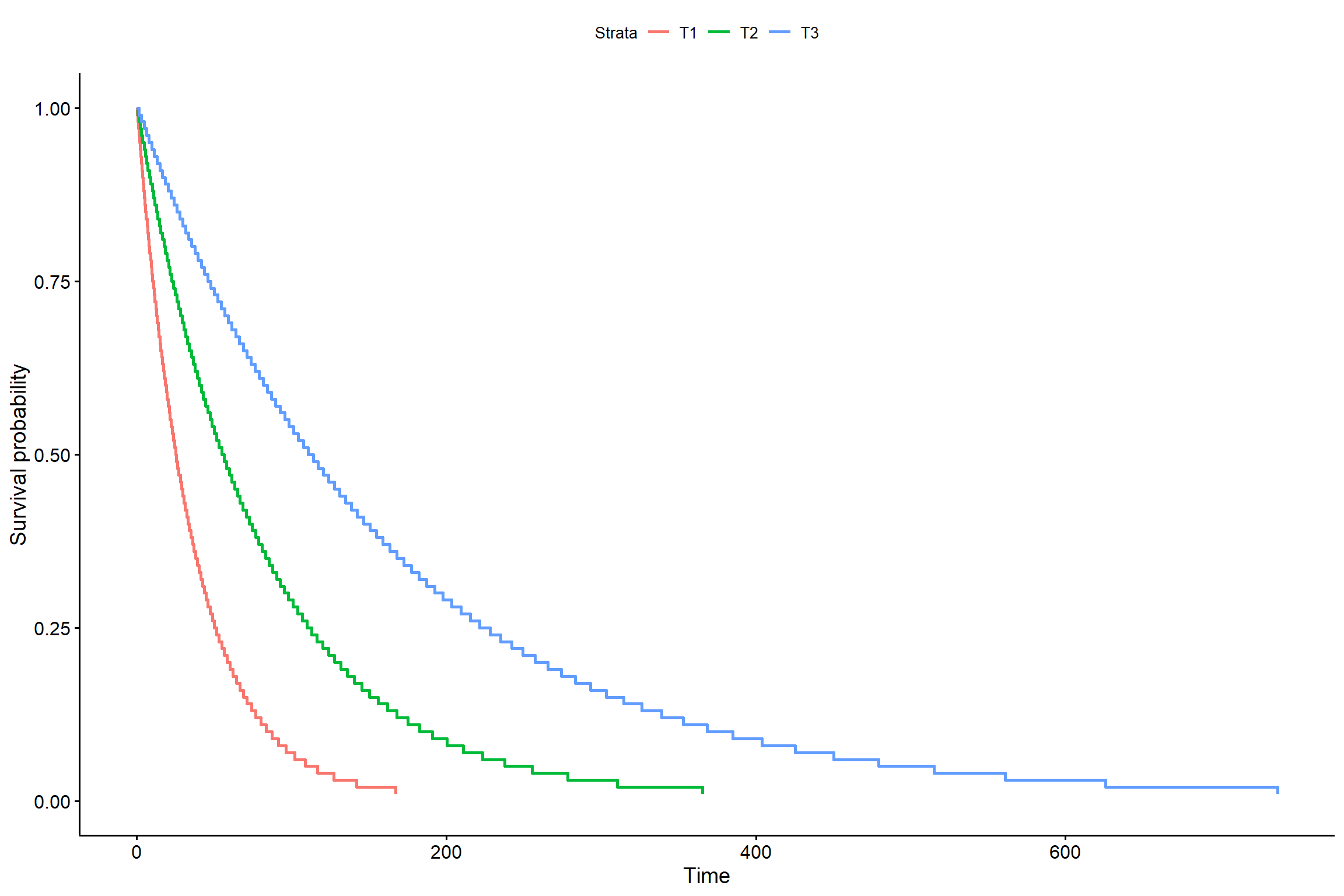  

---

2.5 Distribuição gaussiano

---

2.5.1 Sem considerar tratamentos

KM <- survreg(Surv(tempo,status) ~ 1, dist="gaussian")
summary(KM)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ 1, dist = "gaussian")
##               Value Std. Error    z      p
## (Intercept) 78.8982     5.9303 13.3 <2e-16
## Log(scale)   4.2519     0.0652 65.2 <2e-16
## 
## Scale= 70.2 
## 
## Gaussian distribution
## Loglik(model)= -735.6   Loglik(intercept only)= -735.6
## Number of Newton-Raphson Iterations: 5 
## n= 144

2.5.2 Considerando tratamentos

KM3 <- survreg(Surv(tempo,status) ~ trat, dist="gaussian")
summary(KM3)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ trat, dist = "gaussian")
##               Value Std. Error     z       p
## (Intercept) 36.3750     8.5829  4.24 2.3e-05
## tratT2      37.3906    12.1867  3.07  0.0022
## tratT3      89.7879    12.3737  7.26 4.0e-13
## Log(scale)   4.0854     0.0649 62.96 < 2e-16
## 
## Scale= 59.5 
## 
## Gaussian distribution
## Loglik(model)= -712.5   Loglik(intercept only)= -735.6
##  Chisq= 46.23 on 2 degrees of freedom, p= 9.2e-11 
## Number of Newton-Raphson Iterations: 4 
## n= 144

anova(KM3)

##      Df Deviance Resid. Df    -2*LL     Pr(>Chi)
## NULL NA       NA       142 1471.295           NA
## trat  2 46.22645       140 1425.069 9.163355e-11

t_0 <- predict(KM3, newdata = data.frame(trat = "T1"), type = "lp")
t_1 <- predict(KM3, newdata = data.frame(trat = "T2"),type = "lp")
t_2 <- predict(KM3, newdata = data.frame(trat = "T3"),type = "lp")
x_grid <- 1:400
sur_curves <- sapply(t_0, function(x)survreg.distributions[[KM3$dist]]$density((x - x_grid)/KM3$scale)[, 1])
sur_curves1 <- sapply(t_1, function(x)survreg.distributions[[KM3$dist]]$density((x - x_grid)/KM3$scale)[, 1])
sur_curves2 <- sapply(t_2, function(x)survreg.distributions[[KM3$dist]]$density((x - x_grid)/KM3$scale)[, 1])
matplot(x_grid, sur_curves, type = "l", lty = 1,ylim=c(0,1))
lines(x_grid,sur_curves1,col="red")
lines(x_grid,sur_curves2,col="blue")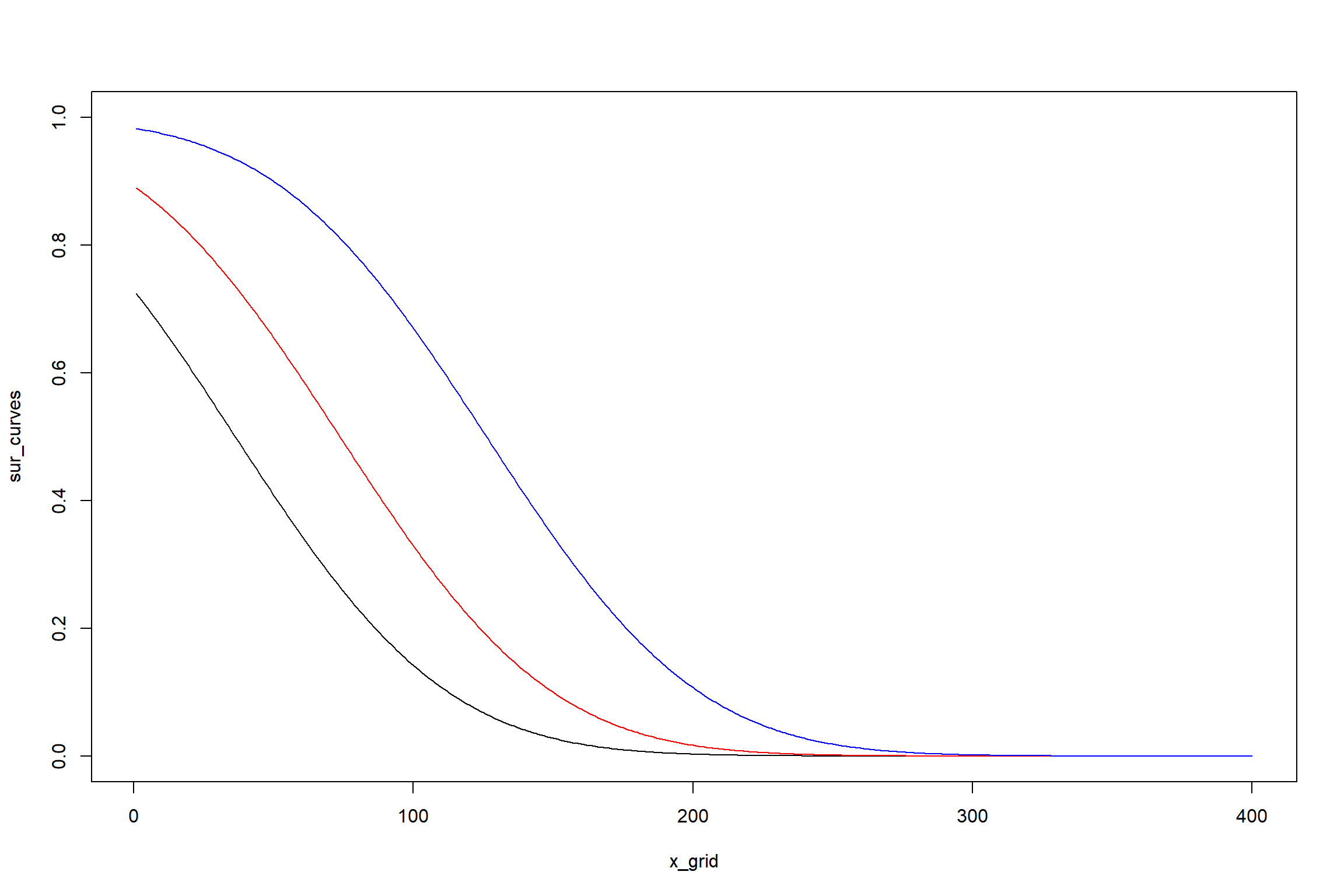

---

2.6 Distribuição logistico

---

2.6.1 Sem considerar tratamentos

KM <- survreg(Surv(tempo,status) ~ 1, dist="logistic")
summary(KM)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ 1, dist = "logistic")
##               Value Std. Error    z      p
## (Intercept) 72.5020     6.3768 11.4 <2e-16
## Log(scale)   3.7594     0.0722 52.0 <2e-16
## 
## Scale= 42.9 
## 
## Logistic distribution
## Loglik(model)= -739.5   Loglik(intercept only)= -739.5
## Number of Newton-Raphson Iterations: 5 
## n= 144

2.6.2 Considerando tratamentos

KM4 <- survreg(Surv(tempo,status) ~ trat, dist="logistic")
summary(KM4)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ trat, dist = "logistic")
##               Value Std. Error     z       p
## (Intercept) 35.4968     7.7296  4.59 4.4e-06
## tratT2      31.3587    12.2695  2.56   0.011
## tratT3      98.9211    12.4589  7.94 2.0e-15
## Log(scale)   3.5544     0.0737 48.20 < 2e-16
## 
## Scale= 35 
## 
## Logistic distribution
## Loglik(model)= -714.3   Loglik(intercept only)= -739.5
##  Chisq= 50.45 on 2 degrees of freedom, p= 1.1e-11 
## Number of Newton-Raphson Iterations: 4 
## n= 144

anova(KM4)

##      Df Deviance Resid. Df    -2*LL     Pr(>Chi)
## NULL NA       NA       142 1479.091           NA
## trat  2 50.45218       140 1428.639 1.107765e-11

t_0 <- predict(KM4, newdata = data.frame(trat = "T1"), type = "lp")
t_1 <- predict(KM4, newdata = data.frame(trat = "T2"),type = "lp")
t_2 <- predict(KM4, newdata = data.frame(trat = "T3"),type = "lp")
x_grid <- 1:400
sur_curves <- sapply(t_0, function(x)survreg.distributions[[KM4$dist]]$density((x - x_grid)/KM4$scale)[, 1])
sur_curves1 <- sapply(t_1, function(x)survreg.distributions[[KM4$dist]]$density((x - x_grid)/KM4$scale)[, 1])
sur_curves2 <- sapply(t_2, function(x)survreg.distributions[[KM4$dist]]$density((x - x_grid)/KM4$scale)[, 1])
matplot(x_grid, sur_curves, type = "l", lty = 1,ylim=c(0,1))
lines(x_grid,sur_curves1,col="red")
lines(x_grid,sur_curves2,col="blue")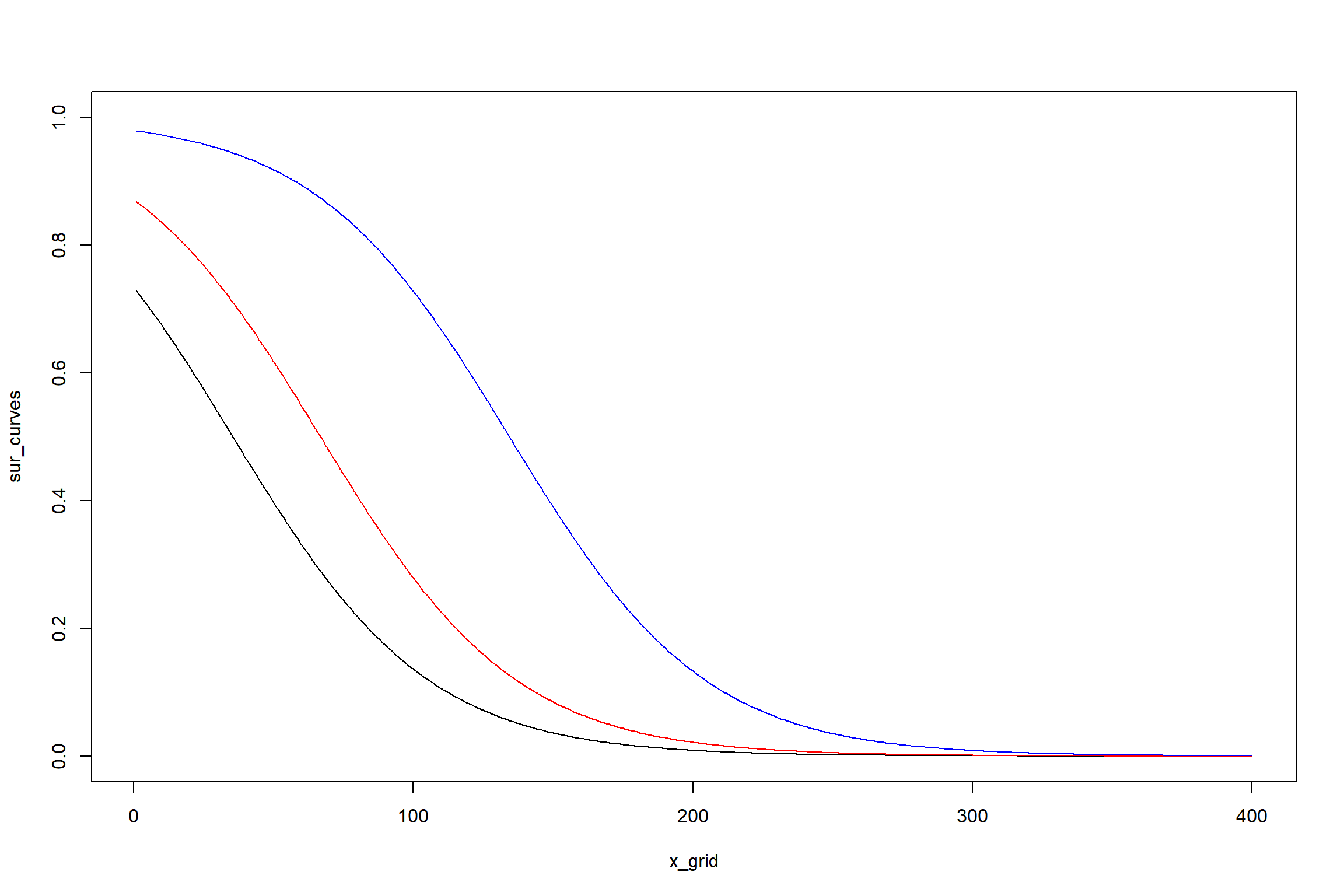

---

2.7 Distribuição Log normal

---

2.7.1 Sem considerar tratamentos

KM <- survreg(Surv(tempo,status) ~ 1, dist="lognormal")
summary(KM)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ 1, dist = "lognormal")
##              Value Std. Error     z       p
## (Intercept) 3.8658     0.1080 35.80 < 2e-16
## Log(scale)  0.2438     0.0648  3.76 0.00017
## 
## Scale= 1.28 
## 
## Log Normal distribution
## Loglik(model)= -681.1   Loglik(intercept only)= -681.1
## Number of Newton-Raphson Iterations: 5 
## n= 144

2.7.2 Considerando tratamentos

KM5 <- survreg(Surv(tempo,status) ~ trat, dist="lognormal")
summary(KM5)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ trat, dist = "lognormal")
##              Value Std. Error     z      p
## (Intercept) 3.2165     0.1655 19.43 <2e-16
## tratT2      0.5650     0.2352  2.40  0.016
## tratT3      1.3925     0.2394  5.82  6e-09
## Log(scale)  0.1369     0.0644  2.12  0.034
## 
## Scale= 1.15 
## 
## Log Normal distribution
## Loglik(model)= -665.4   Loglik(intercept only)= -681.1
##  Chisq= 31.54 on 2 degrees of freedom, p= 1.4e-07 
## Number of Newton-Raphson Iterations: 4 
## n= 144

anova(KM5)

##      Df Deviance Resid. Df    -2*LL     Pr(>Chi)
## NULL NA       NA       142 1362.288           NA
## trat  2 31.54326       140 1330.744 1.414059e-07

s <- seq(.01, .99, by = .01)
t_0 <- predict(KM5, newdata = data.frame(trat = "T1"), type = "quantile", p = s)
t_1 <- predict(KM5, newdata = data.frame(trat = "T2"), type = "quantile", p = s)
t_2 <- predict(KM5, newdata = data.frame(trat = "T3"), type = "quantile", p = s)
smod <- data.frame(time = c(t_0, t_1, t_2), # acrescentar os tratamentos 
                   surv = rep(1 - s, times = 3), # mudar o times
                   strata = rep(c("T1", "T2", "T3"), each = length(s)),
                   upper = NA, lower = NA)
ggsurvplot(smod)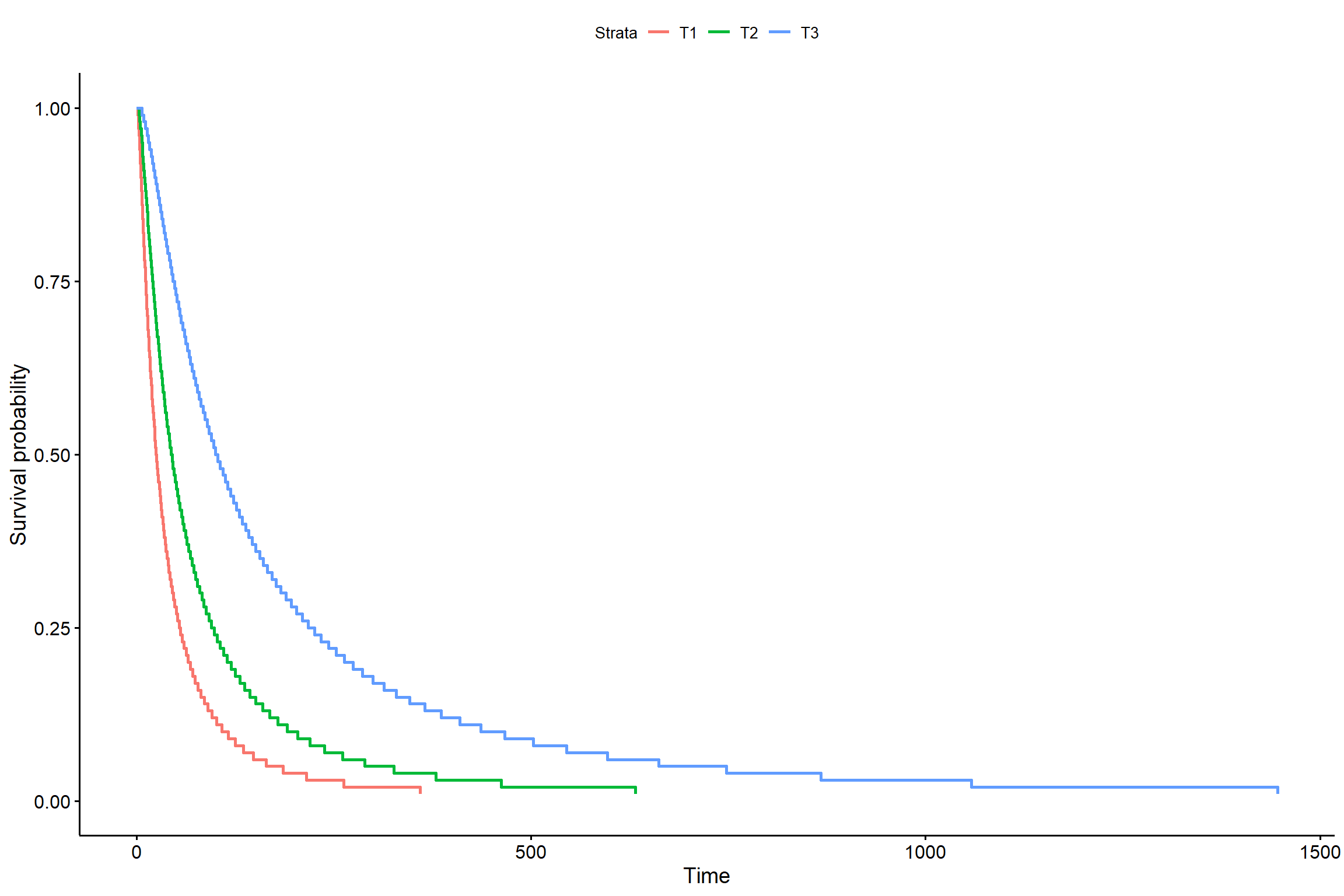  

---

2.8 Distribuição Log-Logístico

---

2.8.1 Sem considerar tratamentos

KM <- survreg(Surv(tempo,status) ~ 1, dist="loglogistic")
summary(KM)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ 1, dist = "loglogistic")
##               Value Std. Error     z      p
## (Intercept)  3.8717     0.1192 32.49 <2e-16
## Log(scale)  -0.2265     0.0711 -3.19 0.0014
## 
## Scale= 0.797 
## 
## Log logistic distribution
## Loglik(model)= -687   Loglik(intercept only)= -687
## Number of Newton-Raphson Iterations: 5 
## n= 144

2.8.2 Considerando tratamentos

KM6 <- survreg(Surv(tempo,status) ~ trat, dist="loglogistic")
summary(KM6)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ trat, dist = "loglogistic")
##               Value Std. Error     z       p
## (Intercept)  3.1947     0.1689 18.92 < 2e-16
## tratT2       0.5839     0.2530  2.31   0.021
## tratT3       1.5687     0.2441  6.43 1.3e-10
## Log(scale)  -0.3709     0.0725 -5.11 3.2e-07
## 
## Scale= 0.69 
## 
## Log logistic distribution
## Loglik(model)= -669.2   Loglik(intercept only)= -687
##  Chisq= 35.64 on 2 degrees of freedom, p= 1.8e-08 
## Number of Newton-Raphson Iterations: 4 
## n= 144

anova(KM6)

##      Df Deviance Resid. Df    -2*LL     Pr(>Chi)
## NULL NA       NA       142 1373.973           NA
## trat  2 35.64462       140 1338.328 1.819156e-08

s <- seq(.01, .99, by = .01)
t_0 <- predict(KM6, newdata = data.frame(trat = "T1"), type = "quantile", p = s)
t_1 <- predict(KM6, newdata = data.frame(trat = "T2"), type = "quantile", p = s)
t_2 <- predict(KM6, newdata = data.frame(trat = "T3"), type = "quantile", p = s)
smod <- data.frame(time = c(t_0, t_1, t_2), # acrescentar os tratamentos 
                   surv = rep(1 - s, times = 3), # mudar o times
                   strata = rep(c("T1", "T2", "T3"), each = length(s)),
                   upper = NA, lower = NA)
ggsurvplot(smod)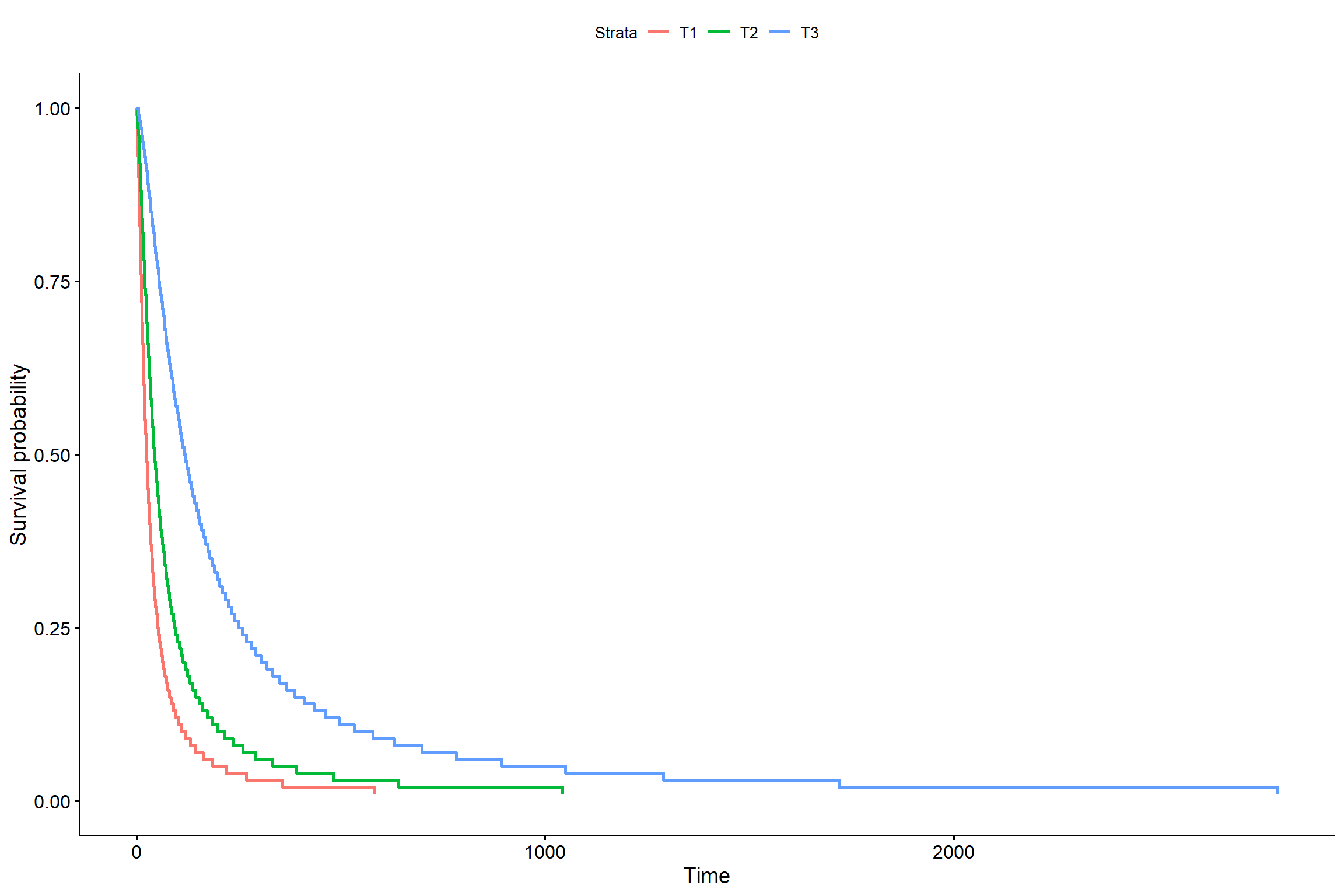  

---

2.9 Distribuição Weibull (default)

---

2.9.1 Sem considerar tratamentos

KM <- survreg(Surv(tempo,status) ~ 1, dist="weibull")
summary(KM)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ 1, dist = "weibull")
##              Value Std. Error     z      p
## (Intercept) 4.4310     0.0969 45.72 <2e-16
## Log(scale)  0.0685     0.0740  0.93   0.35
## 
## Scale= 1.07 
## 
## Weibull distribution
## Loglik(model)= -685.9   Loglik(intercept only)= -685.9
## Number of Newton-Raphson Iterations: 6 
## n= 144

2.9.2 Considerando tratamentos

KM7 <- survreg(Surv(tempo,status) ~ trat, dist="weibull")
summary(KM7)

## 
## Call:
## survreg(formula = Surv(tempo, status) ~ trat, dist = "weibull")
##               Value Std. Error     z       p
## (Intercept)  3.6259     0.1334 27.18 < 2e-16
## tratT2       0.7769     0.1906  4.08 4.6e-05
## tratT3       1.4392     0.2043  7.05 1.8e-12
## Log(scale)  -0.0969     0.0744 -1.30    0.19
## 
## Scale= 0.908 
## 
## Weibull distribution
## Loglik(model)= -663.4   Loglik(intercept only)= -685.9
##  Chisq= 45 on 2 degrees of freedom, p= 1.7e-10 
## Number of Newton-Raphson Iterations: 5 
## n= 144

anova(KM7)

##      Df Deviance Resid. Df    -2*LL     Pr(>Chi)
## NULL NA       NA       142 1371.840           NA
## trat  2 44.99626       140 1326.844 1.695061e-10

s <- seq(.01, .99, by = .01)
t_0 <- predict(KM7, newdata = data.frame(trat = "T1"), type = "quantile", p = s)
t_1 <- predict(KM7, newdata = data.frame(trat = "T2"), type = "quantile", p = s)
t_2 <- predict(KM7, newdata = data.frame(trat = "T3"), type = "quantile", p = s)
smod <- data.frame(time = c(t_0, t_1, t_2), # acrescentar os tratamentos 
                   surv = rep(1 - s, times = 3), # mudar o times
                   strata = rep(c("T1", "T2", "T3"), each = length(s)),
                   upper = NA, lower = NA)
ggsurvplot(smod)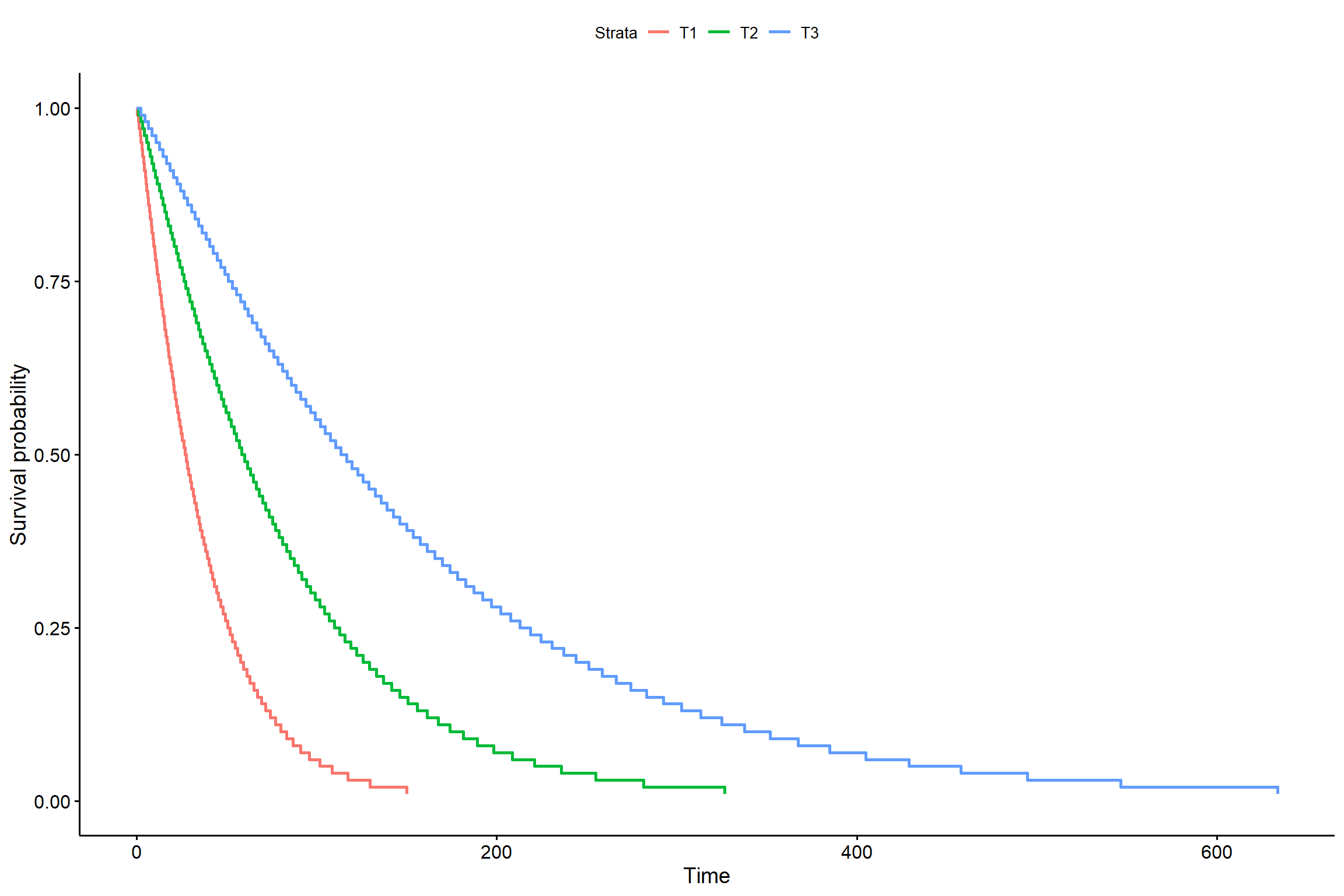  

2.10 Gamma

---

library(flexsurv)
KM10=flexsurvreg(Surv(tempo,status)~trat,dist="gamma")
summary(KM10)

## trat=T1 
##   time         est         lcl        ucl
## 1   10 0.790201487 0.712877981 0.85722852
## 2   24 0.537681788 0.431528186 0.63689279
## 3   48 0.267748022 0.169564617 0.37089704
## 4   72 0.130741530 0.064017122 0.21475910
## 5   96 0.063206831 0.024071450 0.12537705
## 6  120 0.030369861 0.008524038 0.07277707
## 7  144 0.014531118 0.003076532 0.04259751
## 8  168 0.006931519 0.001079952 0.02487986
## 
## trat=T2 
##   time       est        lcl       ucl
## 1   10 0.9055576 0.85145936 0.9442122
## 2   24 0.7671054 0.68524507 0.8391997
## 3   48 0.5650288 0.45737191 0.6620669
## 4   72 0.4110387 0.29508463 0.5172154
## 5   96 0.2969771 0.18954541 0.4003649
## 6  120 0.2136179 0.12107344 0.3109144
## 7  144 0.1531754 0.07761403 0.2415220
## 8  168 0.1095770 0.04976384 0.1875847
## 
## trat=T3 
##   time       est       lcl       ucl
## 1   10 0.9552715 0.9210188 0.9762314
## 2   24 0.8838874 0.8241471 0.9263987
## 3   48 0.7645536 0.6769355 0.8314138
## 4   72 0.6563859 0.5522481 0.7442904
## 5   96 0.5610497 0.4459237 0.6637055
## 6  120 0.4781342 0.3582737 0.5901244
## 7  144 0.4065841 0.2849254 0.5227047
## 8  168 0.3451603 0.2277240 0.4635648

plot(KM10,col=c(1,2,3))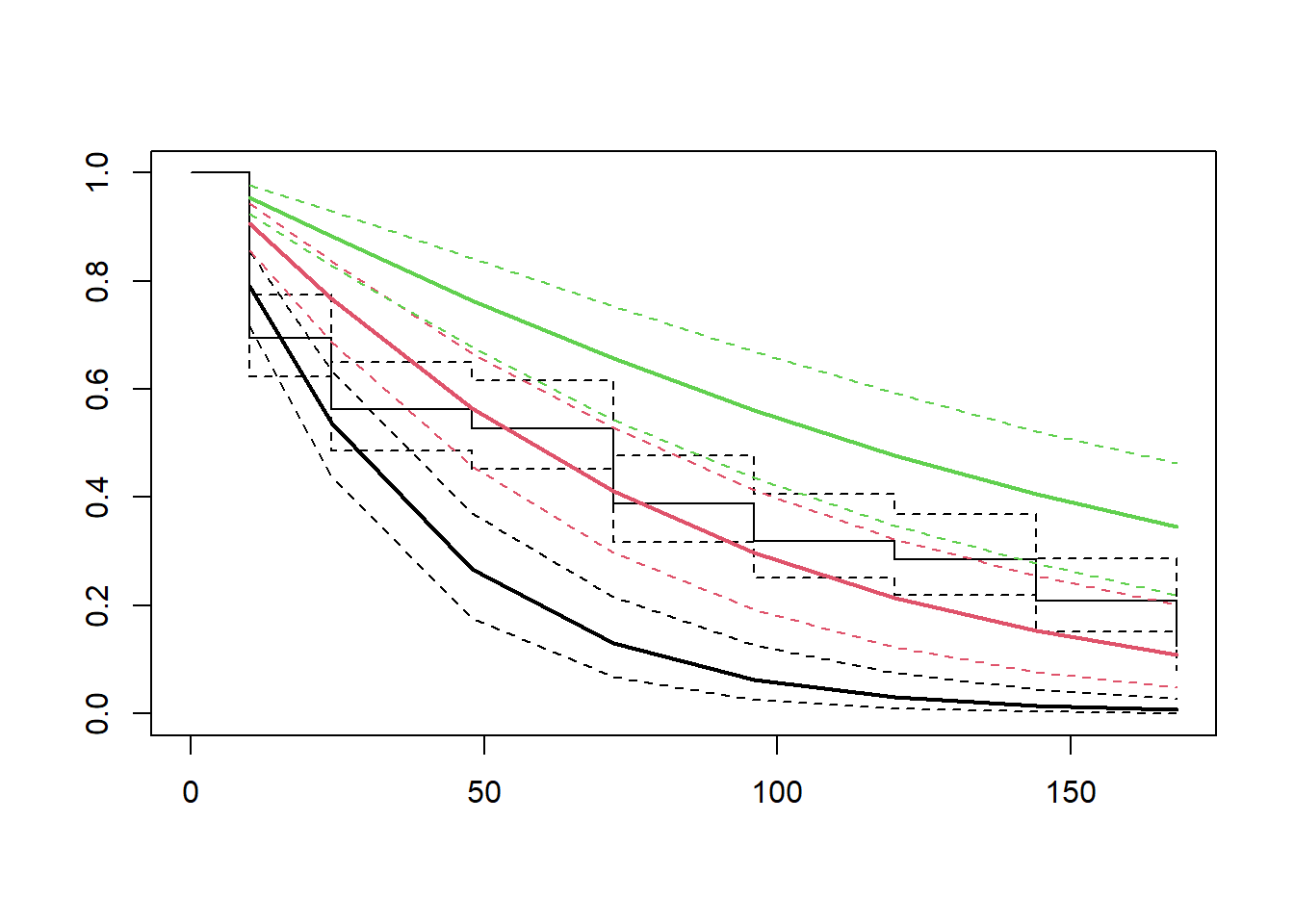

---

2.11 Método semi-paramétrico de Cox

---

Serve para um modelo de regressão de riscos proporcionais de Cox. Variáveis dependentes do tempo, estratos dependentes do tempo, vários eventos por assunto e outras extensões são incorporadas usando a formulação do processo de contagem de Andersen e Gill.

Reference: Andersen, P. and Gill, R. (1982). Cox’s regression model for counting processes, a large sample study. Annals of Statistics 10, 1100-1120.

2.11.1 Sem considerar tratamentos

KM <- coxph(Surv(tempo,status) ~ 1)
summary(KM)

## Call:  coxph(formula = Surv(tempo, status) ~ 1)
## 
## Null model
##   log likelihood= -538.6621 
##   n= 144

2.11.2 Considerando tratamentos

KM8 <- coxph(Surv(tempo,status) ~ strata(trat),data=dados)
summary(KM8)

## Call:  coxph(formula = Surv(tempo, status) ~ strata(trat), data = dados)
## 
## Null model
##   log likelihood= -394.6821 
##   n= 144

library(ggfortify)
autoplot(survfit(KM8),conf.int = F)+theme_classic()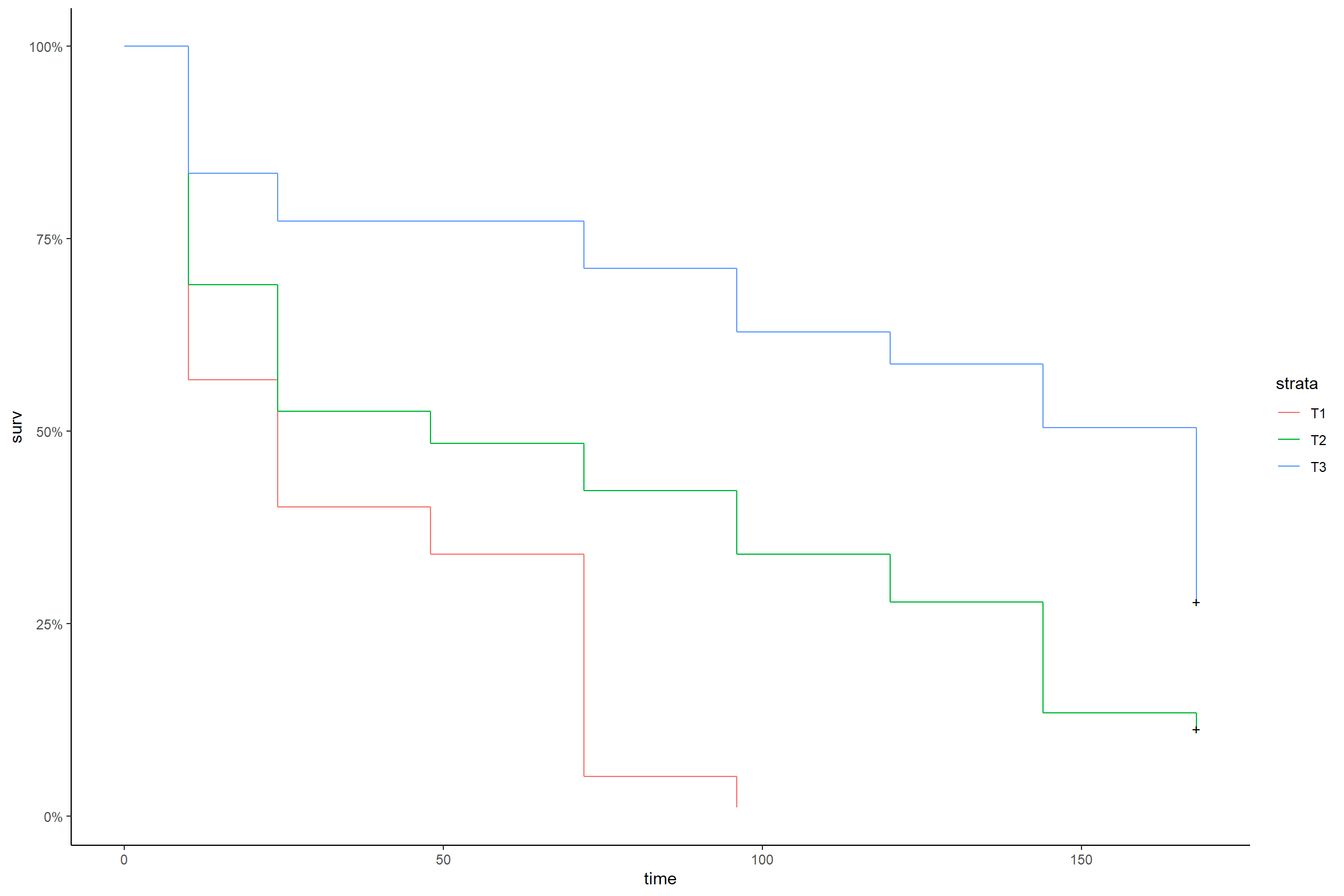

---

2.12 Modelo de riscos proporcionais de COX

---

Mostra as taxas de risco (HR) derivadas do modelo para todas as covariáveis incluídas na fórmula coxph. Resumidamente, uma FC> 1 indica um risco aumentado de morte (de acordo com a definição de h(t)) se uma condição específica for atendida por um paciente. Uma FC <1, por outro lado, indica uma diminuição do risco.

2.12.1 Considerando trat

library(forestmodel)
colnames(dados)=c("Treatments","tempo","status")
fit.coxph <- coxph(Surv(tempo, status) ~ Treatments, data = dados)
#ggforest(fit.coxph, data = dados)
print(forest_model(fit.coxph, limits=log( c(0.05, 5))))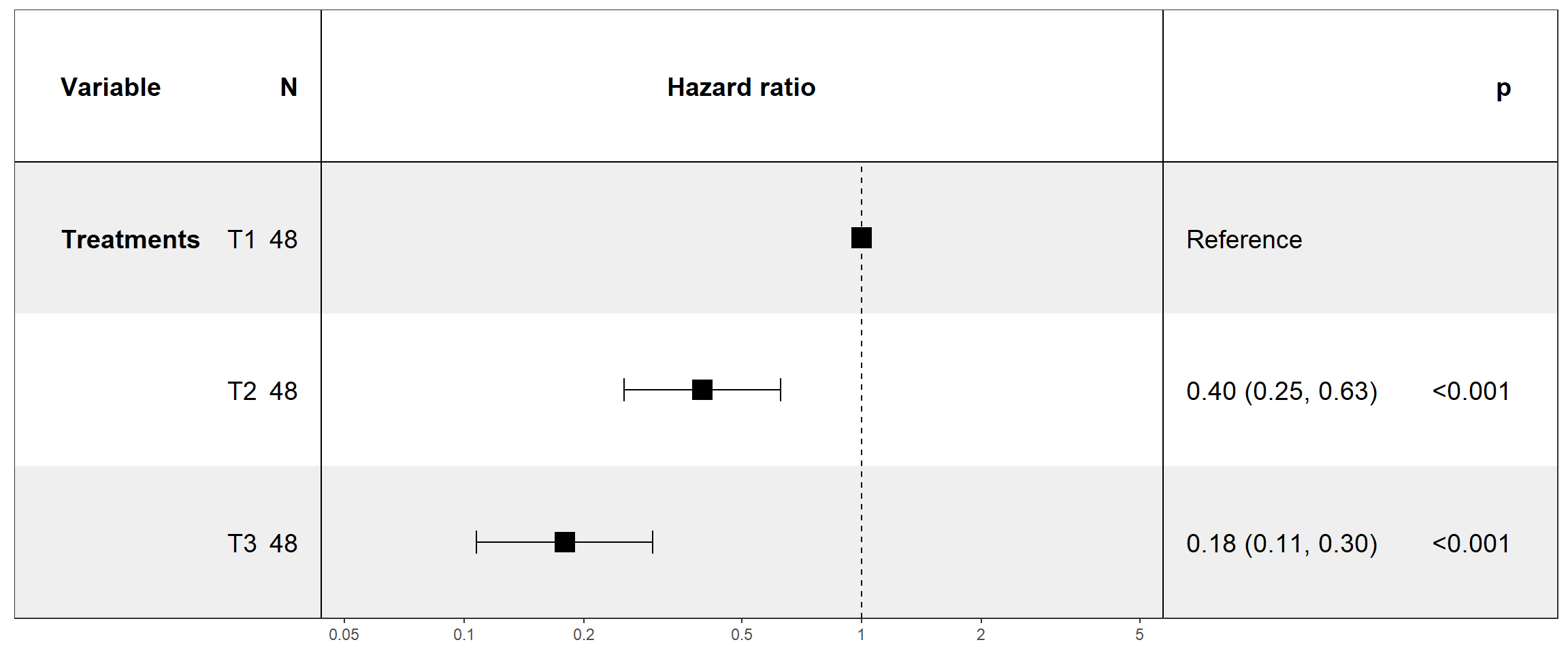

2.13 Critério de inferência de Akaike

library(car)
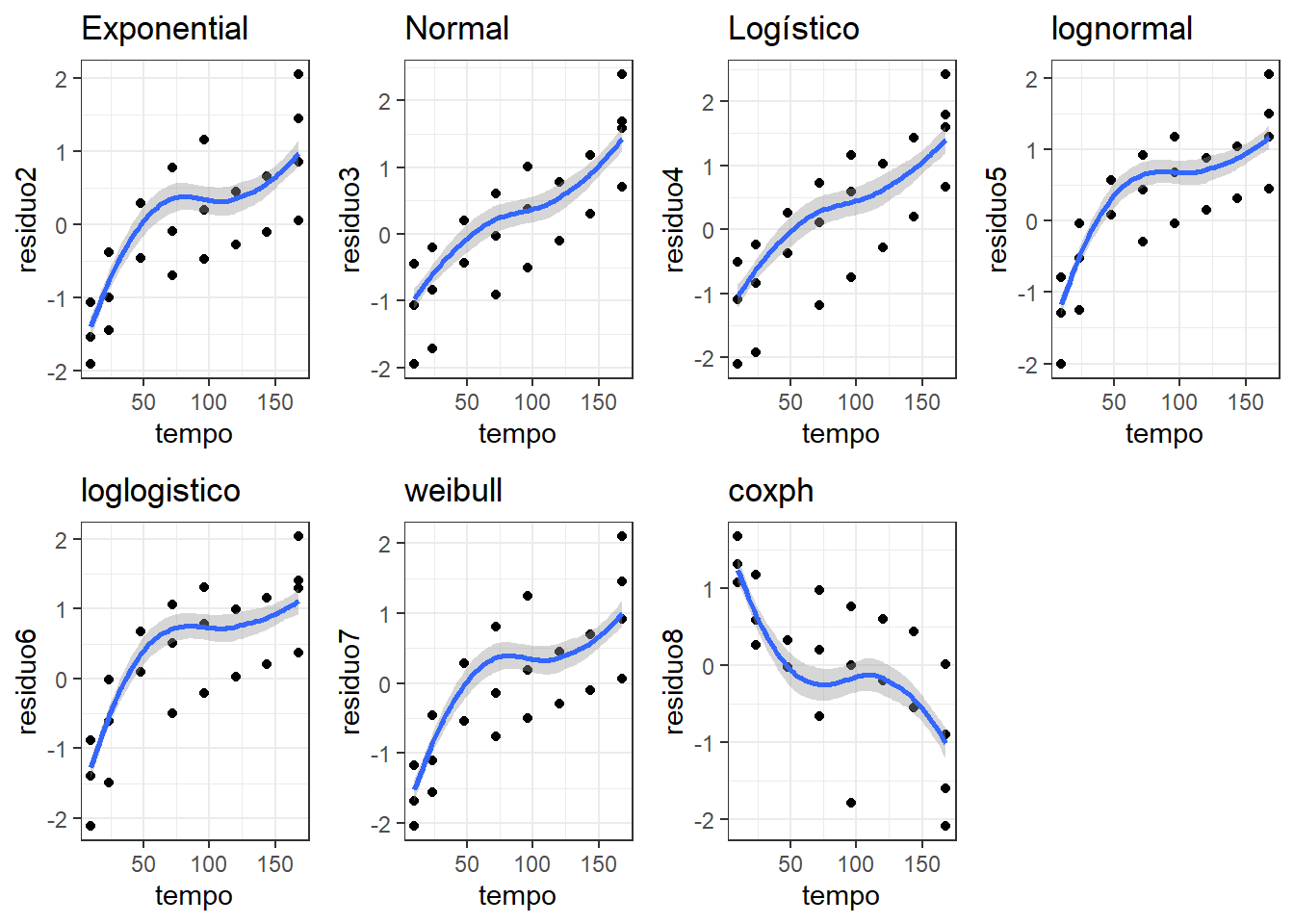
AIC(KM2) # exponencial

## [1] 1334.477

AIC(KM3) # normal

## [1] 1433.069

AIC(KM4) # logistico

## [1] 1436.639

AIC(KM5) # lognormal

## [1] 1338.744

AIC(KM6) # loglogistic

## [1] 1346.328

AIC(KM7) # weibull

## [1] 1334.844

AIC(KM8) # coxph

## [1] 789.3642

2.14 Resíduo

residuo2 <- residuals(KM2, type = "deviance")
g2=ggplot(data = dados, mapping = aes(x = tempo, y = residuo2)) +
    geom_point() + labs(title="Exponential")+
    geom_smooth() +
    theme_bw() + theme(legend.key = element_blank())
residuo3 <- residuals(KM3, type = "deviance")
g3=ggplot(data = dados, mapping = aes(x = tempo, y = residuo3)) +
    geom_point() + labs(title="Normal")+
    geom_smooth() +
    theme_bw() + theme(legend.key = element_blank())
residuo4 <- residuals(KM4, type = "deviance")
g4=ggplot(data = dados, mapping = aes(x = tempo, y = residuo4)) +
    geom_point() + labs(title="Logístico")+
    geom_smooth() +
    theme_bw() + theme(legend.key = element_blank())
residuo5 <- residuals(KM5, type = "deviance")
g5=ggplot(data = dados, mapping = aes(x = tempo, y = residuo5)) +
    geom_point() + labs(title="lognormal")+
    geom_smooth() +
    theme_bw() + theme(legend.key = element_blank())
residuo6 <- residuals(KM6, type = "deviance")
g6=ggplot(data = dados, mapping = aes(x = tempo, y = residuo6)) +
    geom_point() + labs(title="loglogistico")+
    geom_smooth() +
    theme_bw() + theme(legend.key = element_blank())
residuo7 <- residuals(KM7, type = "deviance")
g7=ggplot(data = dados, mapping = aes(x = tempo, y = residuo7)) +
    geom_point() + labs(title="weibull")+
    geom_smooth() +
    theme_bw() + theme(legend.key = element_blank())
residuo8 <- residuals(KM8, type = "deviance")
g8=ggplot(data = dados, mapping = aes(x = tempo, y = residuo8)) +
    geom_point() + labs(title="coxph")+
    geom_smooth() +
    theme_bw() + theme(legend.key = element_blank())
library(gridExtra)
grid.arrange(g2,g3,g4,g5,g6,g7,g8,ncol=4)