3 Modelo linear generalizado
3.1 Conjunto de dados
Considera um conjunto de dados simulados de germinação com oito repetições e quatro tratamento qualitativos. Conforme a regra de análise de sementes, em um teste de germinação é estabelecido a quantidade mínima de 50 sementes por rolo de papel. Logo, sabemos que a quantidade máxima de cada repetição e de 50 sementes.
trat=rep(paste("T",1:4),e=8)
germ=c(33,35,34,30,38,30,37,30,36,38,34,38,38,38,35,35,30,15,31,17,25,24,24,18,27,20,28,35,30,30,30,29)3.2 Modelo linear generalizado
No R, podemos realizar a entrada dos dados de duas formas. Pela proporção ou por dados dicotomizados (Respostas do tipo 0 ou 1).
Nosso exemplo usaremos pela proporção.
modelo=glm(cbind(germ,50-germ)~trat, family=binomial)Explicação: germ é nossa resposta, ou seja, total de sementes germinadas (ou podemos chamar de total de sucessos na repetição). O valor 50 indica o total de observações na repetição (Deve ser conhecido). trat é nossa variável explicativa qualitativa, binomial é a distrbuição provável que estamos considerando.
3.3 Análise de deviance
summary(modelo)##
## Call:
## glm(formula = cbind(germ, 50 - germ) ~ trat, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.4488 -0.5500 0.2359 0.4838 2.2701
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.6969 0.1061 6.566 5.16e-11 ***
## tratT 2 0.2977 0.1548 1.924 0.05437 .
## tratT 3 -0.8572 0.1460 -5.870 4.36e-09 ***
## tratT 4 -0.4048 0.1466 -2.762 0.00574 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 108.818 on 31 degrees of freedom
## Residual deviance: 38.676 on 28 degrees of freedom
## AIC: 182.75
##
## Number of Fisher Scoring iterations: 3anova(modelo, test="Chisq")## Analysis of Deviance Table
##
## Model: binomial, link: logit
##
## Response: cbind(germ, 50 - germ)
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 31 108.818
## trat 3 70.142 28 38.676 3.979e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 13.4 Diagnóstico
par(mfrow=c(2,2))
plot(modelo)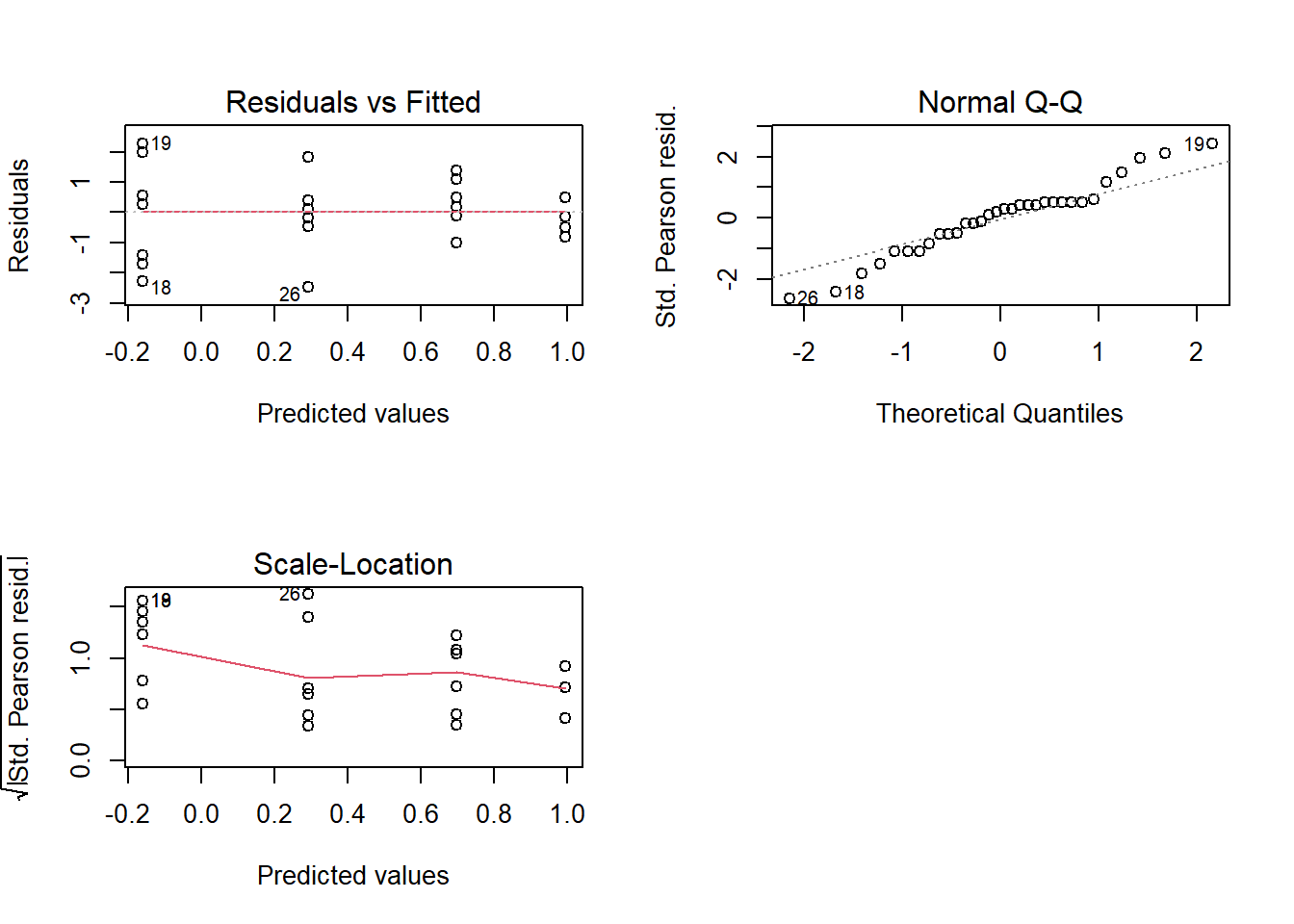
3.5 Halfnormaplot
hnp::hnp(modelo, print.on=T)## Binomial model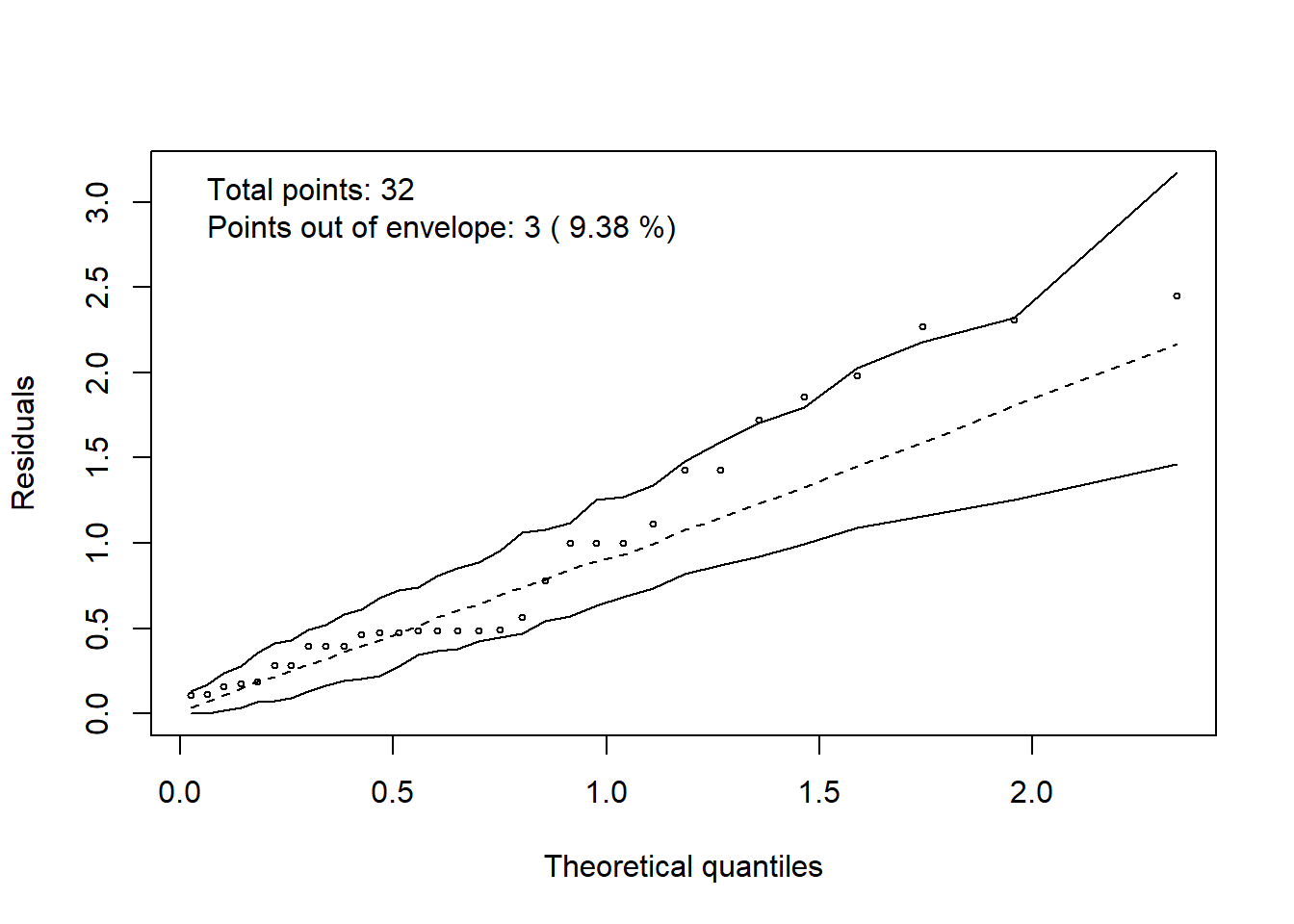
3.6 Constrastes
library(emmeans)
media=emmeans(modelo,~trat)3.7 Retornando a função logistica
medfin=regrid(media)
library(multcompView)
library(multcomp)
cld(medfin, alpha=0.05, Letters=letters, decreasing=FALSE, adjust="tukey")## trat prob SE df asymp.LCL asymp.UCL .group
## T 3 0.460 0.0249 Inf 0.398 0.522 a
## T 4 0.573 0.0247 Inf 0.511 0.634 b
## T 1 0.667 0.0236 Inf 0.609 0.726 c
## T 2 0.730 0.0222 Inf 0.675 0.785 c
##
## Confidence level used: 0.95
## Conf-level adjustment: sidak method for 4 estimates
## P value adjustment: tukey method for comparing a family of 4 estimates
## significance level used: alpha = 0.053.8 Supondo que não sabemos o total de cada repetição
Nesse caso, vamos optar pela distribuição poisson
modelo=glm(germ~trat, family=poisson)3.9 Análise de deviance
summary(modelo)##
## Call:
## glm(formula = germ ~ trat, family = poisson)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7823 -0.3347 0.1574 0.2550 1.5832
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 3.50781 0.06120 57.318 < 2e-16 ***
## tratT 2 0.08951 0.08468 1.057 0.290496
## tratT 3 -0.37231 0.09581 -3.886 0.000102 ***
## tratT 4 -0.15353 0.09007 -1.705 0.088274 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 46.061 on 31 degrees of freedom
## Residual deviance: 18.017 on 28 degrees of freedom
## AIC: 193.41
##
## Number of Fisher Scoring iterations: 4anova(modelo, test="Chisq")## Analysis of Deviance Table
##
## Model: poisson, link: log
##
## Response: germ
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 31 46.061
## trat 3 28.045 28 18.017 3.555e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 13.10 Diagnóstico
par(mfrow=c(2,2))
plot(modelo)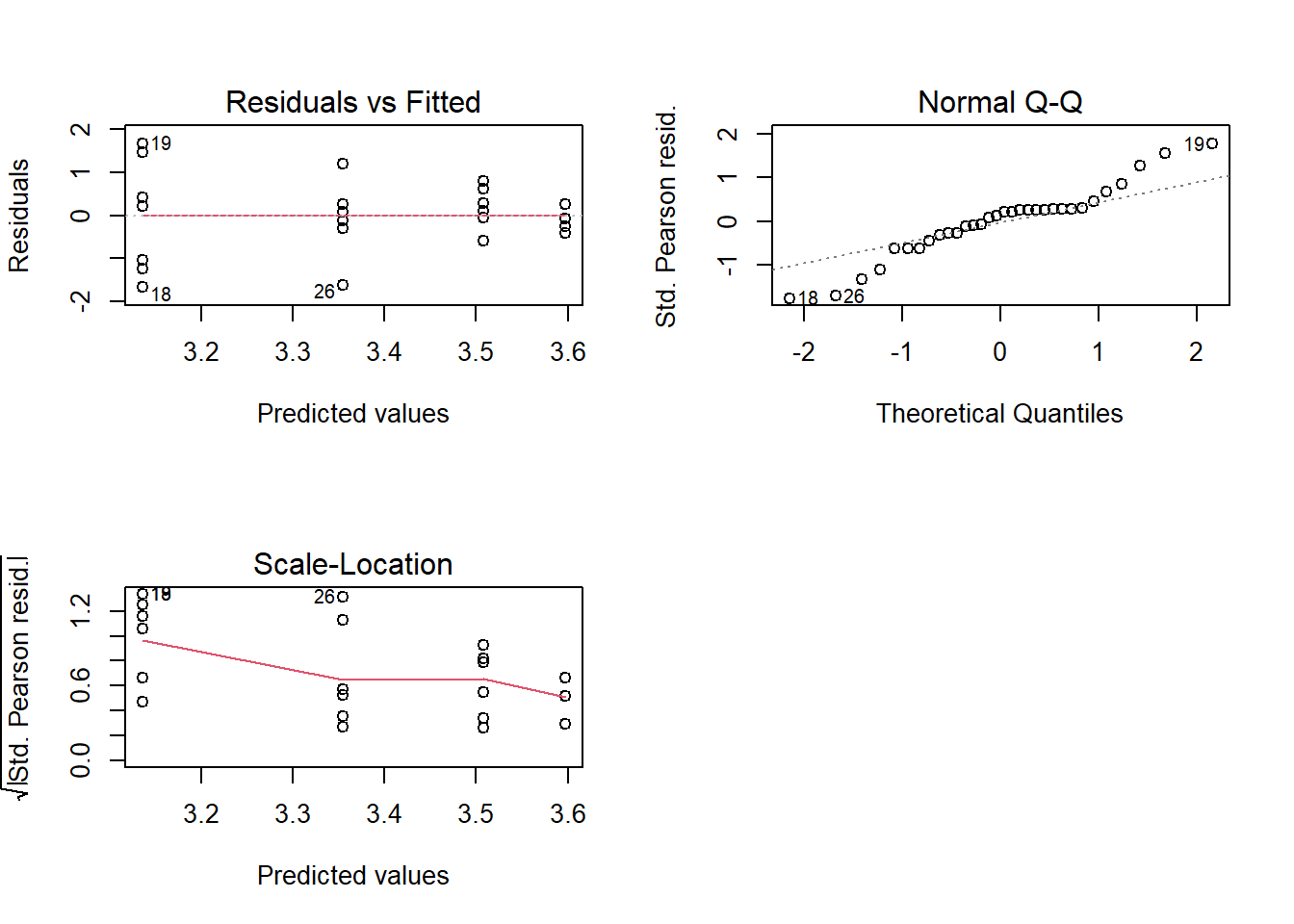
3.11 Halfnormaplot
hnp::hnp(modelo, print.on=T)## Poisson model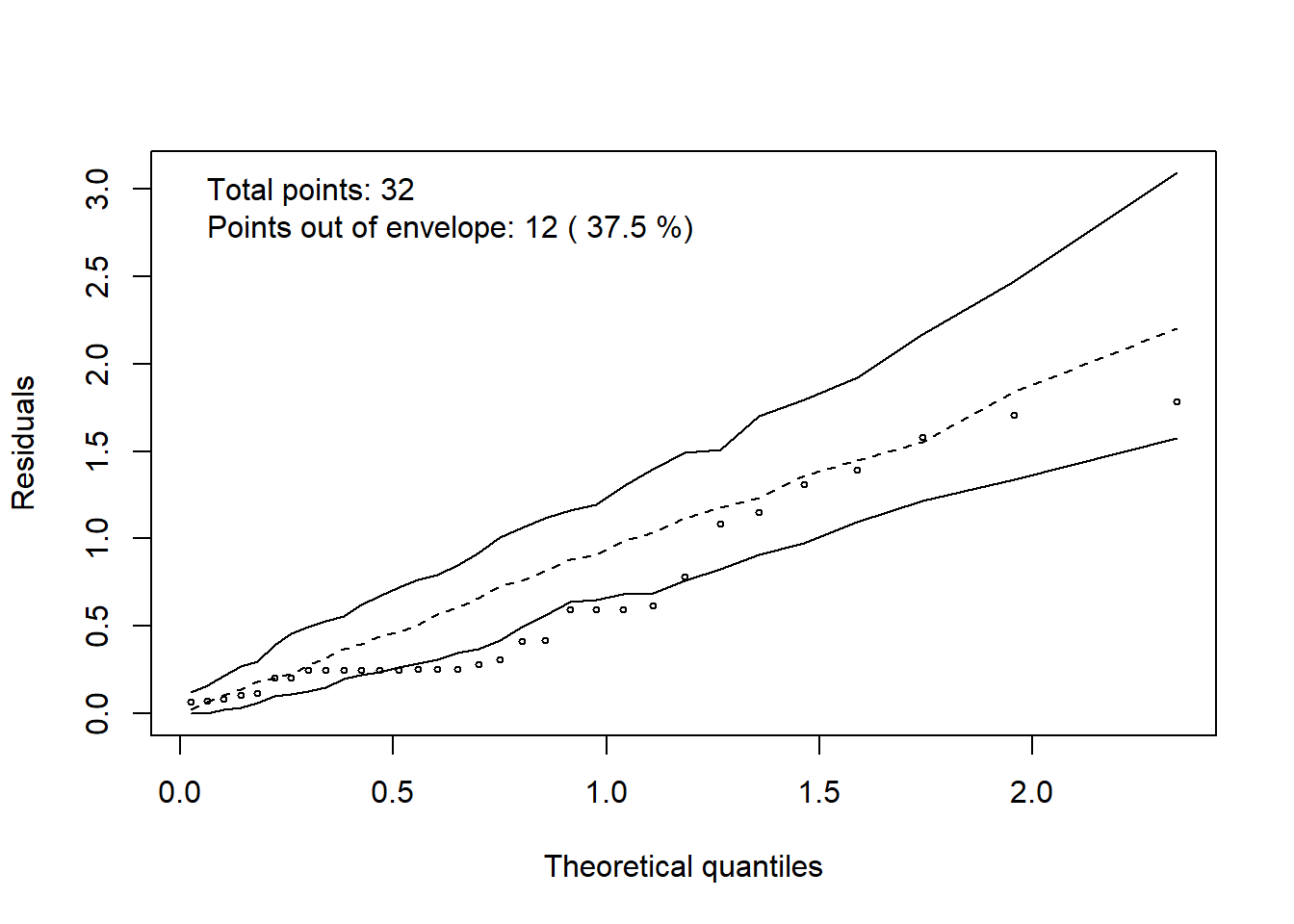
3.12 Constrastes
library(emmeans)
media=emmeans(modelo,~trat)3.13 Retornando a função logistica
medfin=regrid(media)
library(multcompView)
library(multcomp)
cld(medfin, alpha=0.05, Letters=letters, decreasing=FALSE, adjust="tukey")## trat rate SE df asymp.LCL asymp.UCL .group
## T 3 23.0 1.70 Inf 18.8 27.2 a
## T 4 28.6 1.89 Inf 23.9 33.3 ab
## T 1 33.4 2.04 Inf 28.3 38.5 bc
## T 2 36.5 2.14 Inf 31.2 41.8 c
##
## Confidence level used: 0.95
## Conf-level adjustment: sidak method for 4 estimates
## P value adjustment: tukey method for comparing a family of 4 estimates
## significance level used: alpha = 0.053.14 Analisando sobredispersão
library(AER)
dispersiontest(modelo, trafo=1) ##
## Overdispersion test
##
## data: modelo
## z = -2.8129, p-value = 0.9975
## alternative hypothesis: true alpha is greater than 0
## sample estimates:
## alpha
## -0.4488216## se for menor que 0,01 há sbredispersão, nesse caso usar quasipoissonCaso fosse menor que 0,01 ou 0,05, podemos testar a distribuição quasipoisson. Vamos treinar, ainda que não seja necessário.
modelo=glm(germ~trat, family=quasipoisson)3.15 Análise de deviance
summary(modelo)##
## Call:
## glm(formula = germ ~ trat, family = quasipoisson)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7823 -0.3347 0.1574 0.2550 1.5832
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.50781 0.04857 72.219 < 2e-16 ***
## tratT 2 0.08951 0.06720 1.332 0.1937
## tratT 3 -0.37231 0.07604 -4.896 3.69e-05 ***
## tratT 4 -0.15353 0.07148 -2.148 0.0405 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 0.6299182)
##
## Null deviance: 46.061 on 31 degrees of freedom
## Residual deviance: 18.017 on 28 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4anova(modelo, test="Chisq")## Analysis of Deviance Table
##
## Model: quasipoisson, link: log
##
## Response: germ
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 31 46.061
## trat 3 28.045 28 18.017 1.17e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 13.16 Diagnóstico
par(mfrow=c(2,2))
plot(modelo)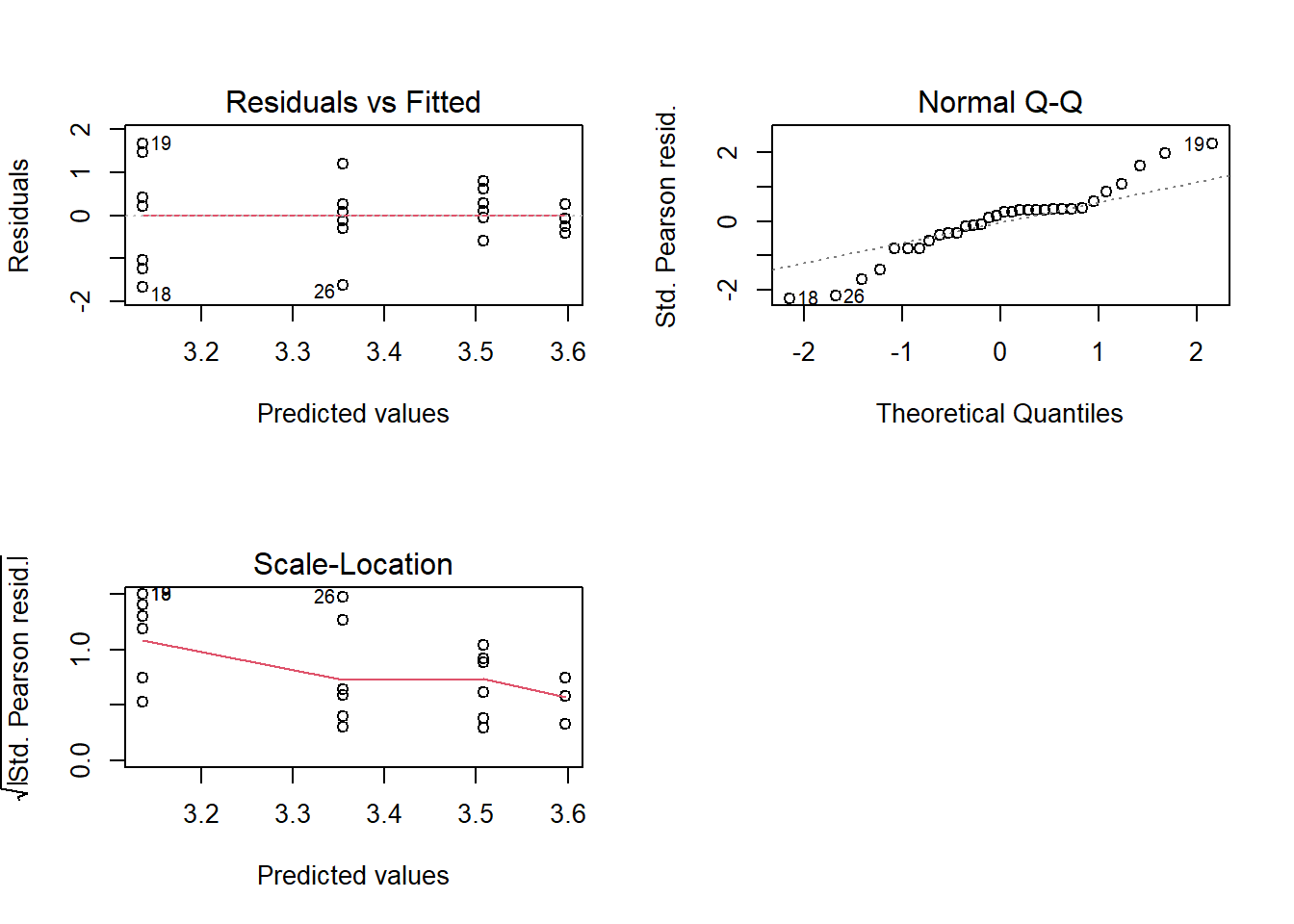
3.17 Halfnormaplot
hnp::hnp(modelo, print.on=T)## Quasi-Poisson model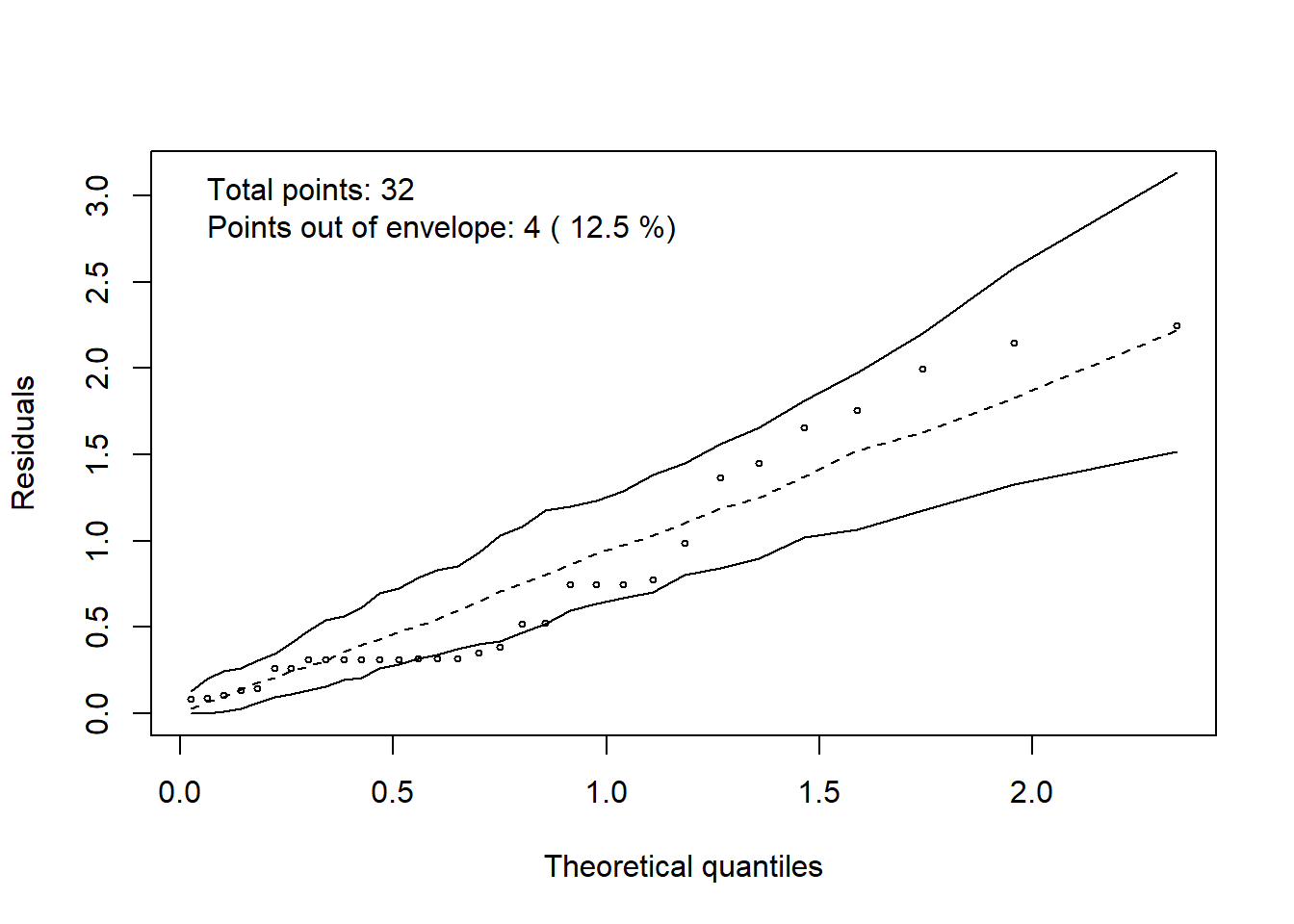
3.18 Constrastes
library(emmeans)
media=emmeans(modelo,~trat)3.19 Retornando a função logistica
medfin=regrid(media)
library(multcompView)
library(multcomp)
cld(medfin, alpha=0.05, Letters=letters, decreasing=FALSE, adjust="tukey")## trat rate SE df asymp.LCL asymp.UCL .group
## T 3 23.0 1.35 Inf 19.6 26.4 a
## T 4 28.6 1.50 Inf 24.9 32.4 b
## T 1 33.4 1.62 Inf 29.3 37.4 bc
## T 2 36.5 1.70 Inf 32.3 40.7 c
##
## Confidence level used: 0.95
## Conf-level adjustment: sidak method for 4 estimates
## P value adjustment: tukey method for comparing a family of 4 estimates
## significance level used: alpha = 0.053.20 Distribuição quasibinomial
quasibin<-glm(cbind(germ,50-germ)~trat, family = quasibinomial)3.21 Análise de deviance
summary(modelo)##
## Call:
## glm(formula = germ ~ trat, family = quasipoisson)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7823 -0.3347 0.1574 0.2550 1.5832
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.50781 0.04857 72.219 < 2e-16 ***
## tratT 2 0.08951 0.06720 1.332 0.1937
## tratT 3 -0.37231 0.07604 -4.896 3.69e-05 ***
## tratT 4 -0.15353 0.07148 -2.148 0.0405 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 0.6299182)
##
## Null deviance: 46.061 on 31 degrees of freedom
## Residual deviance: 18.017 on 28 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4anova(modelo, test="Chisq")## Analysis of Deviance Table
##
## Model: quasipoisson, link: log
##
## Response: germ
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 31 46.061
## trat 3 28.045 28 18.017 1.17e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 13.22 Diagnóstico
par(mfrow=c(2,2))
plot(modelo)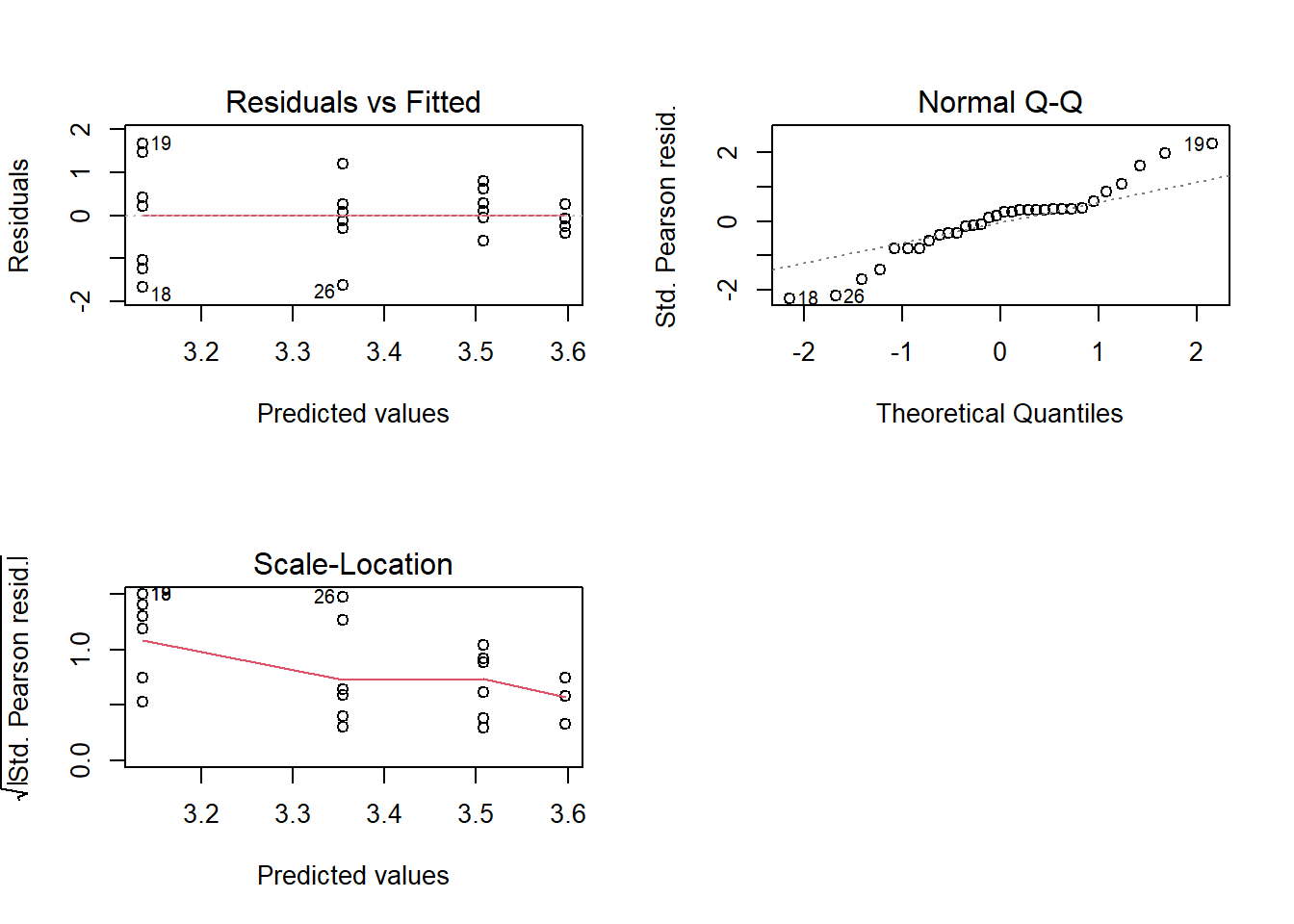
3.23 Halfnormaplot
hnp::hnp(modelo, print.on=T)## Quasi-Poisson model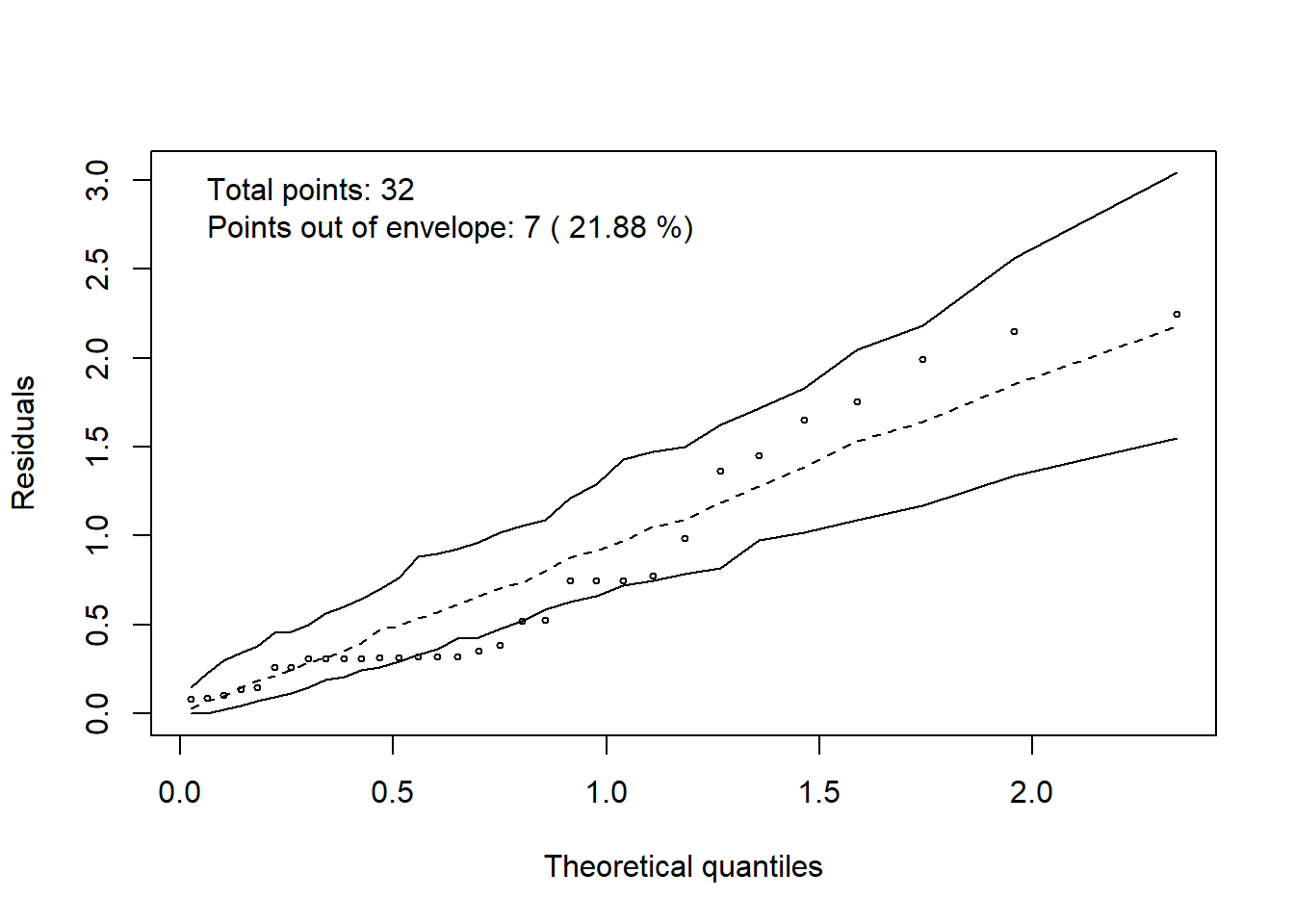
3.24 Constrastes
library(emmeans)
media=emmeans(modelo,~trat)
summary(pairs(media), type = "response")## contrast ratio SE df null z.ratio p.value
## T 1 / T 2 0.914 0.0615 Inf 1 -1.332 0.5425
## T 1 / T 3 1.451 0.1103 Inf 1 4.896 <.0001
## T 1 / T 4 1.166 0.0833 Inf 1 2.148 0.1382
## T 2 / T 3 1.587 0.1186 Inf 1 6.182 <.0001
## T 2 / T 4 1.275 0.0893 Inf 1 3.469 0.0029
## T 3 / T 4 0.803 0.0631 Inf 1 -2.784 0.0275
##
## P value adjustment: tukey method for comparing a family of 4 estimates
## Tests are performed on the log scale3.25 Retornando a função logistica
medfin=regrid(media)
library(multcompView)
library(multcomp)
cld(medfin, alpha=0.05, Letters=letters, decreasing=FALSE, adjust="tukey")## trat rate SE df asymp.LCL asymp.UCL .group
## T 3 23.0 1.35 Inf 19.6 26.4 a
## T 4 28.6 1.50 Inf 24.9 32.4 b
## T 1 33.4 1.62 Inf 29.3 37.4 bc
## T 2 36.5 1.70 Inf 32.3 40.7 c
##
## Confidence level used: 0.95
## Conf-level adjustment: sidak method for 4 estimates
## P value adjustment: tukey method for comparing a family of 4 estimates
## significance level used: alpha = 0.053.26 Fatorial qualitativo e quantitativo
Supondo um outro exemplo de um experimento em esquema fatorial 2 x 5, em que o primeiro fator e qualitativo e o segundo fator quantitativo com 5 doses (2, 4, 6, 8, 10) e três repetições cada. Total de semenetes e conhecido e o valor e 30.
resp=c(0,0,0,3,3,2,6,6,5,17,18,14,25,26,23,
0,1,0,1,1,2,15,14,15,15,16,16,20,20,19)
f1=rep(c("T1","T2"),e=15) ## fator qualitativo
d=rep(c(2,4,6,8,10),e=3,2) ## dose como numerico
D=factor(d) ## considerando dose como fator3.27 Modelo
Vamos considerar os dois fatores como qualitativos
bin=glm(cbind(resp,30-resp)~f1*D, family = binomial)3.28 Deviance
summary(bin)##
## Call:
## glm(formula = cbind(resp, 30 - resp) ~ f1 * D, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.8532 -0.2951 0.1217 0.1590 0.9375
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -23.14 6757.51 -0.003 0.997
## f1T2 18.65 6757.51 0.003 0.998
## D4 20.81 6757.51 0.003 0.998
## D6 21.68 6757.51 0.003 0.997
## D8 23.31 6757.51 0.003 0.997
## D10 24.67 6757.51 0.004 0.997
## f1T2:D4 -19.39 6757.51 -0.003 0.998
## f1T2:D6 -17.24 6757.51 -0.003 0.998
## f1T2:D8 -18.74 6757.51 -0.003 0.998
## f1T2:D10 -19.54 6757.51 -0.003 0.998
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 397.0255 on 29 degrees of freedom
## Residual deviance: 5.6398 on 20 degrees of freedom
## AIC: 108.6
##
## Number of Fisher Scoring iterations: 19anova(bin, test="Chisq")## Analysis of Deviance Table
##
## Model: binomial, link: logit
##
## Response: cbind(resp, 30 - resp)
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 29 397.03
## f1 1 0.24 28 396.78 0.6215
## D 4 363.46 24 33.33 < 2.2e-16 ***
## f1:D 4 27.69 20 5.64 1.443e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1referencia <- ref_grid(bin)
referencia ## Aqui deve aparecer os niveis dos fatores, se dose so aparecer 1, está errado## 'emmGrid' object with variables:
## f1 = T1, T2
## D = 2, 4, 6, 8, 10
## Transformation: "logit"3.29 Teste de comparação
Se não fosse um fator quantitativo, podemos fazer assim:
media <- emmeans(bin, ~f1|D)
medfin<-regrid(media)
cld(medfin, alpha=0.05, Letters=letters, adjust="tukey")## D = 2:
## f1 prob SE df asymp.LCL asymp.UCL .group
## T1 0.0000 6.00e-07 Inf -1.40e-06 1.40e-06 a
## T2 0.0111 1.10e-02 Inf -1.36e-02 3.58e-02 a
##
## D = 4:
## f1 prob SE df asymp.LCL asymp.UCL .group
## T2 0.0444 2.17e-02 Inf -4.14e-03 9.30e-02 a
## T1 0.0889 3.00e-02 Inf 2.18e-02 1.56e-01 a
##
## D = 6:
## f1 prob SE df asymp.LCL asymp.UCL .group
## T1 0.1889 4.13e-02 Inf 9.66e-02 2.81e-01 a
## T2 0.4889 5.27e-02 Inf 3.71e-01 6.07e-01 b
##
## D = 8:
## f1 prob SE df asymp.LCL asymp.UCL .group
## T2 0.5222 5.27e-02 Inf 4.04e-01 6.40e-01 a
## T1 0.5444 5.25e-02 Inf 4.27e-01 6.62e-01 a
##
## D = 10:
## f1 prob SE df asymp.LCL asymp.UCL .group
## T2 0.6556 5.01e-02 Inf 5.44e-01 7.68e-01 a
## T1 0.8222 4.03e-02 Inf 7.32e-01 9.12e-01 b
##
## Confidence level used: 0.95
## Conf-level adjustment: sidak method for 2 estimates
## significance level used: alpha = 0.05media <- emmeans(bin, ~D|f1)
medfin<-regrid(media)
cld(medfin, alpha=0.05, Letters=letters, adjust="tukey")## f1 = T1:
## D prob SE df asymp.LCL asymp.UCL .group
## 2 0.0000 6.00e-07 Inf -1.60e-06 1.60e-06 a
## 4 0.0889 3.00e-02 Inf 1.18e-02 1.66e-01 b
## 6 0.1889 4.13e-02 Inf 8.29e-02 2.95e-01 b
## 8 0.5444 5.25e-02 Inf 4.10e-01 6.79e-01 c
## 10 0.8222 4.03e-02 Inf 7.19e-01 9.26e-01 d
##
## f1 = T2:
## D prob SE df asymp.LCL asymp.UCL .group
## 2 0.0111 1.10e-02 Inf -1.73e-02 3.95e-02 a
## 4 0.0444 2.17e-02 Inf -1.14e-02 1.00e-01 a
## 6 0.4889 5.27e-02 Inf 3.54e-01 6.24e-01 b
## 8 0.5222 5.27e-02 Inf 3.87e-01 6.57e-01 b
## 10 0.6556 5.01e-02 Inf 5.27e-01 7.84e-01 b
##
## Confidence level used: 0.95
## Conf-level adjustment: sidak method for 5 estimates
## P value adjustment: tukey method for comparing a family of 5 estimates
## significance level used: alpha = 0.053.30 Regressão
Como há interação entre os fatores, necessitamos construir duas curvas, vejamos:
3.31 Dividindo o conjunto de dados
resp1=resp[1:15] ## resposta de T1, nesse caso as observações de T1 estão na posição de 1 a 15
resp2=resp[16:30] ## resposta de T2, nesse caso as observações de T2 estão na posição de 16 a 30
d=d[1:15] ## cortando dose, nesse caso somente uma vez é necessário3.32 modelo para T1
bin1=glm(cbind(resp1,30-resp1)~d, family = binomial)
summary(bin1)##
## Call:
## glm(formula = cbind(resp1, 30 - resp1) ~ d, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.9384 -0.7855 -0.1458 0.4803 0.8687
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -5.66100 0.51900 -10.91 <2e-16 ***
## d 0.72347 0.06751 10.72 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 223.1818 on 14 degrees of freedom
## Residual deviance: 6.8923 on 13 degrees of freedom
## AIC: 50.895
##
## Number of Fisher Scoring iterations: 43.33 modelo para T2
bin2=glm(cbind(resp2,30-resp2)~d, family = binomial)
summary(bin2)##
## Call:
## glm(formula = cbind(resp2, 30 - resp2) ~ d, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.8205 -1.5467 -0.9111 0.1884 2.4892
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.89248 0.37250 -10.449 <2e-16 ***
## d 0.49464 0.05016 9.862 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 173.600 on 14 degrees of freedom
## Residual deviance: 34.827 on 13 degrees of freedom
## AIC: 81.781
##
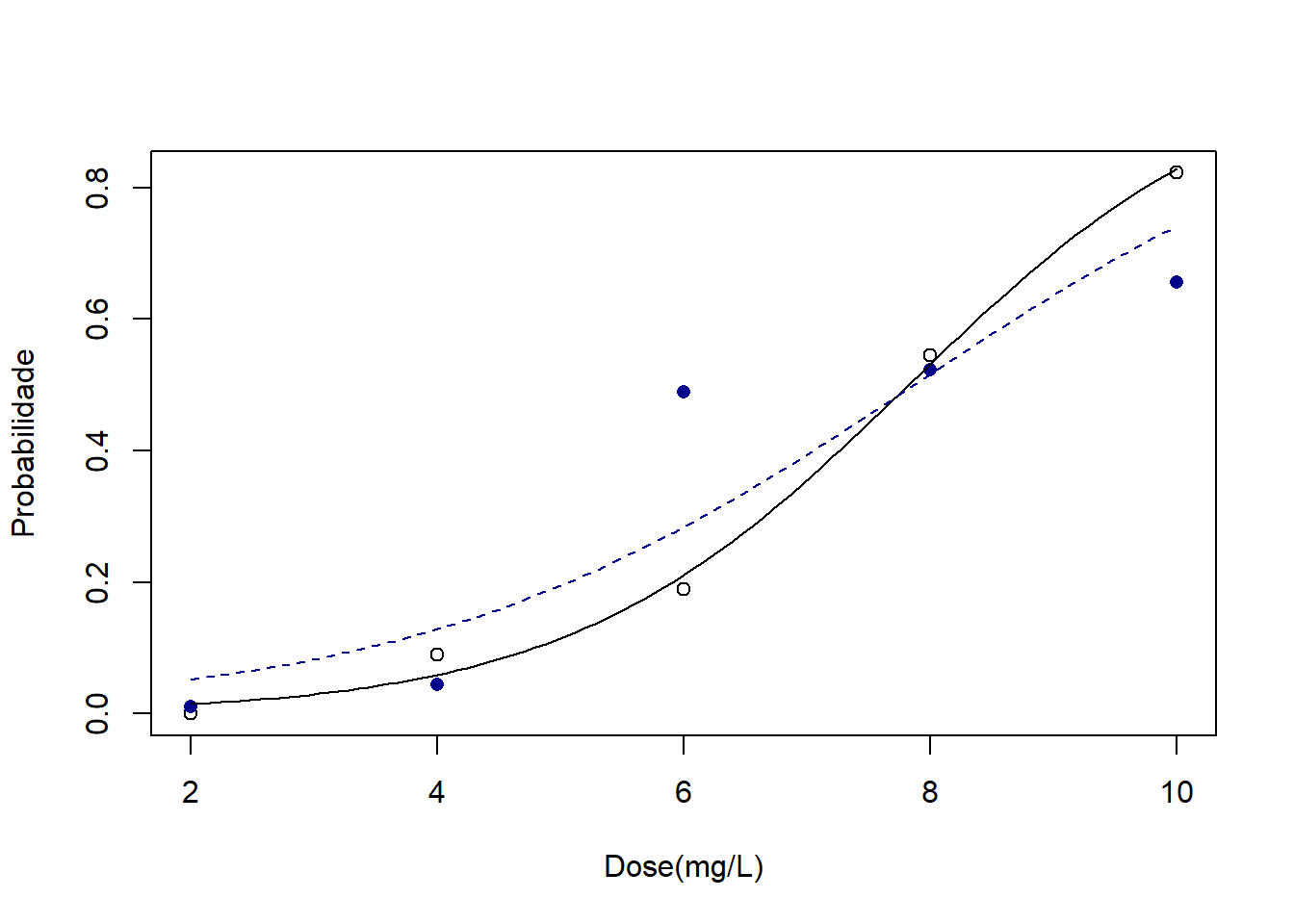
## Number of Fisher Scoring iterations: 53.34 Gráfico
3.34.1 Calculando vetores
med1=tapply(resp1/30, d, mean)
med2=tapply(resp2/30, d, mean)
DOSE=c(2,4,6,8,10)3.34.2 Gráfico final
plot(med1~DOSE,xlab="Dose(mg/L)",ylab="Probabilidade")
points(med2~DOSE,pch=16,col="darkblue")
curve(predict(bin1,data.frame(d=x),type="resp"),add=TRUE) ## curva de T1
##points(d,fitted(bin1),pch=20)
curve(predict(bin2,data.frame(d=x),type="resp"),add=TRUE, lty=2,col="darkblue") ## Curva de T2