15 Componentes principais
A análise de Componentes Principais é um método utilizado para reduzir a dimensão do problema em componentes não correlacionadas que são combinações lineares das variáveis originais. O número dessas componentes é menor ou igual a quantidade de variáveis originais. Esse método é útil quando o número de variáveis em estudo é muito grande.
15.1 Pacote ggforfity
15.1.1 Conjunto de dados
dados <- iris[c(1, 2, 3, 4)]15.1.2 Calculando a PCA
(pca=prcomp(dados,scale. = T))## Standard deviations (1, .., p=4):
## [1] 1,7083611 0,9560494 0,3830886 0,1439265
##
## Rotation (n x k) = (4 x 4):
## PC1 PC2 PC3 PC4
## Sepal.Length 0,5210659 -0,37741762 0,7195664 0,2612863
## Sepal.Width -0,2693474 -0,92329566 -0,2443818 -0,1235096
## Petal.Length 0,5804131 -0,02449161 -0,1421264 -0,8014492
## Petal.Width 0,5648565 -0,06694199 -0,6342727 0,523597115.1.3 Dispersão com os autovalores
library(ggfortify)
autoplot(pca,data=iris)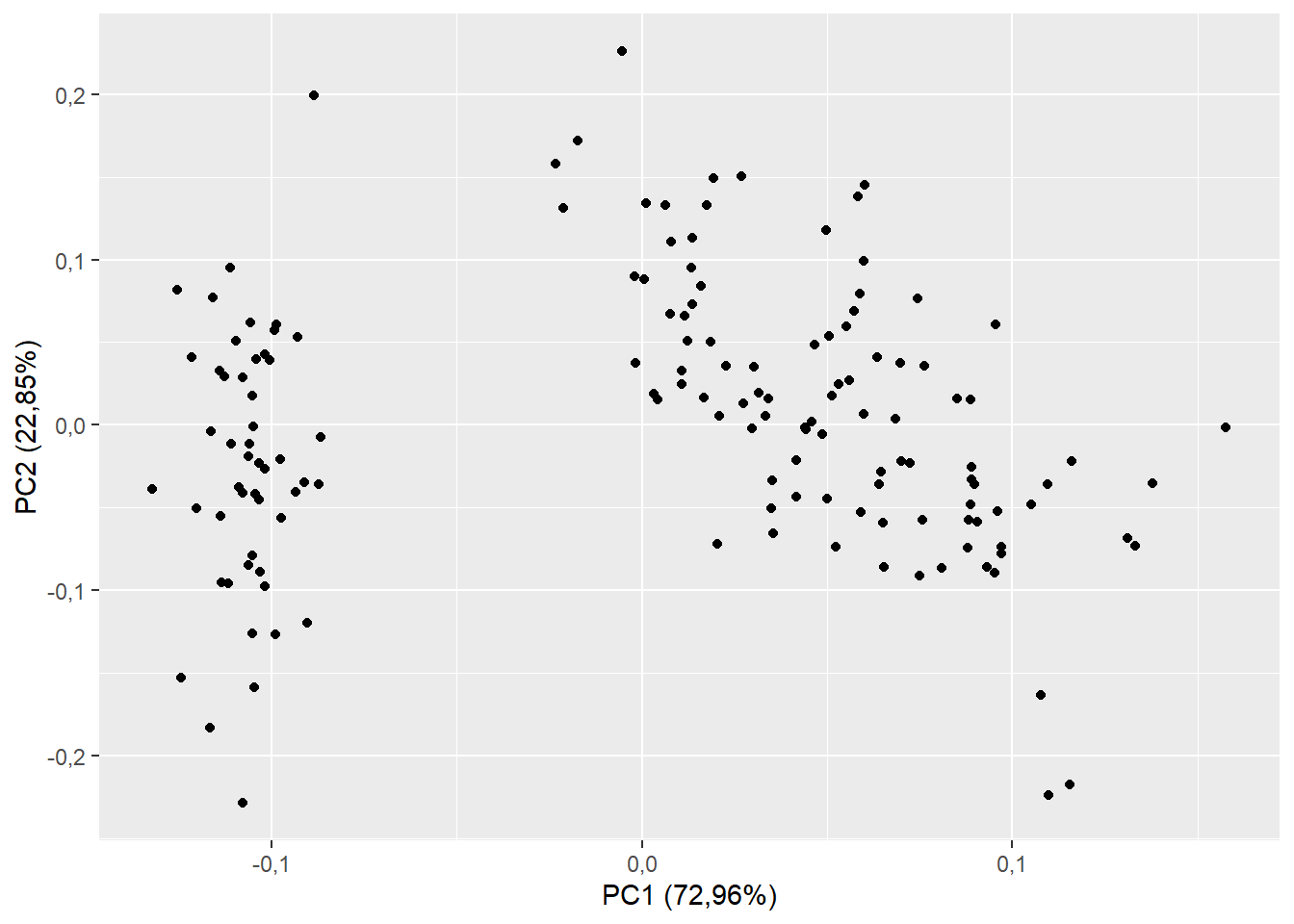
15.1.4 Agrupando por espécies
Obs. a coluna de “Species” está na dataset iris
autoplot(pca,data=iris,colour="Species")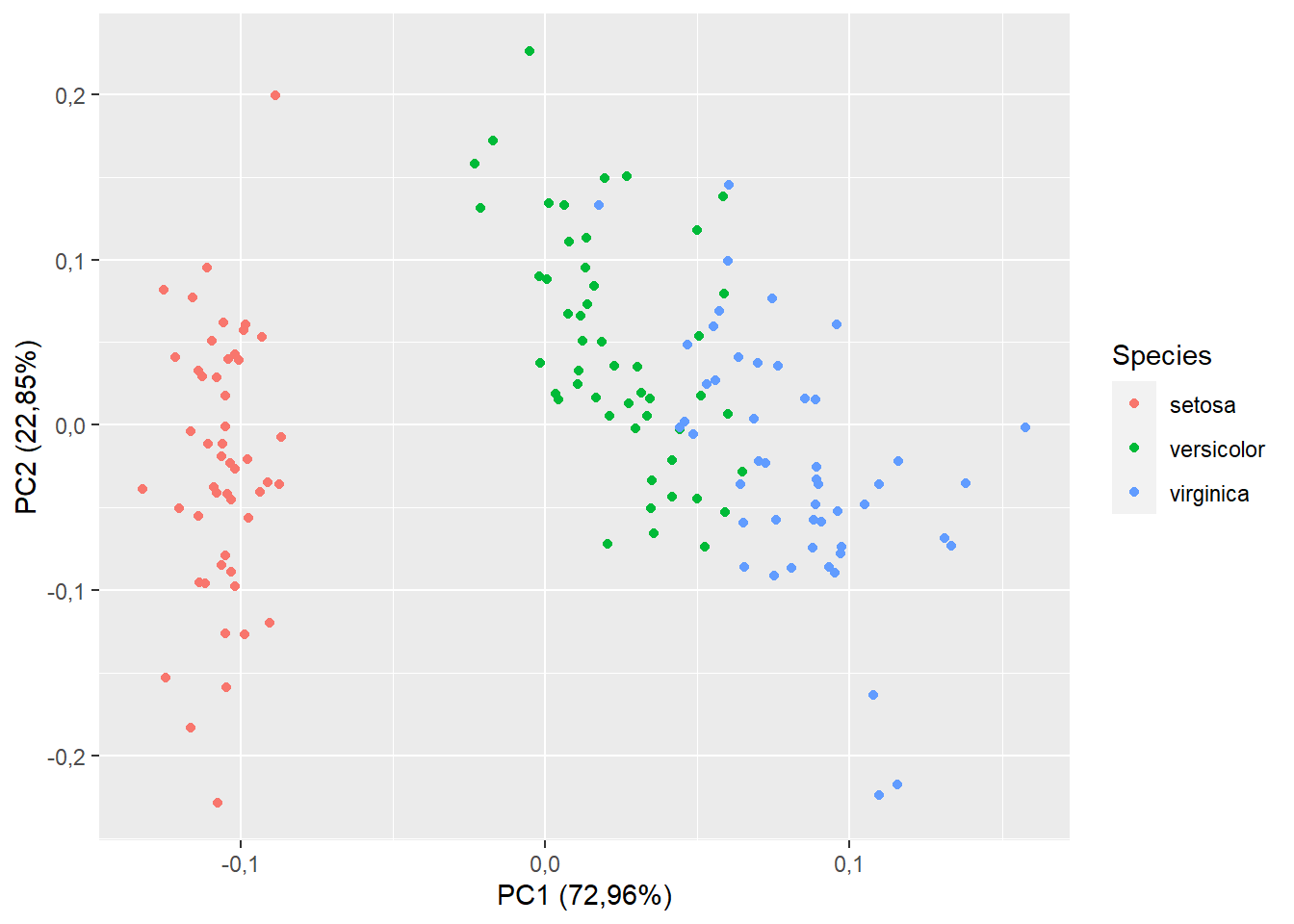
15.1.5 Vetor das respostas
autoplot(pca,
data=iris,
colour="Species",
loadings=T)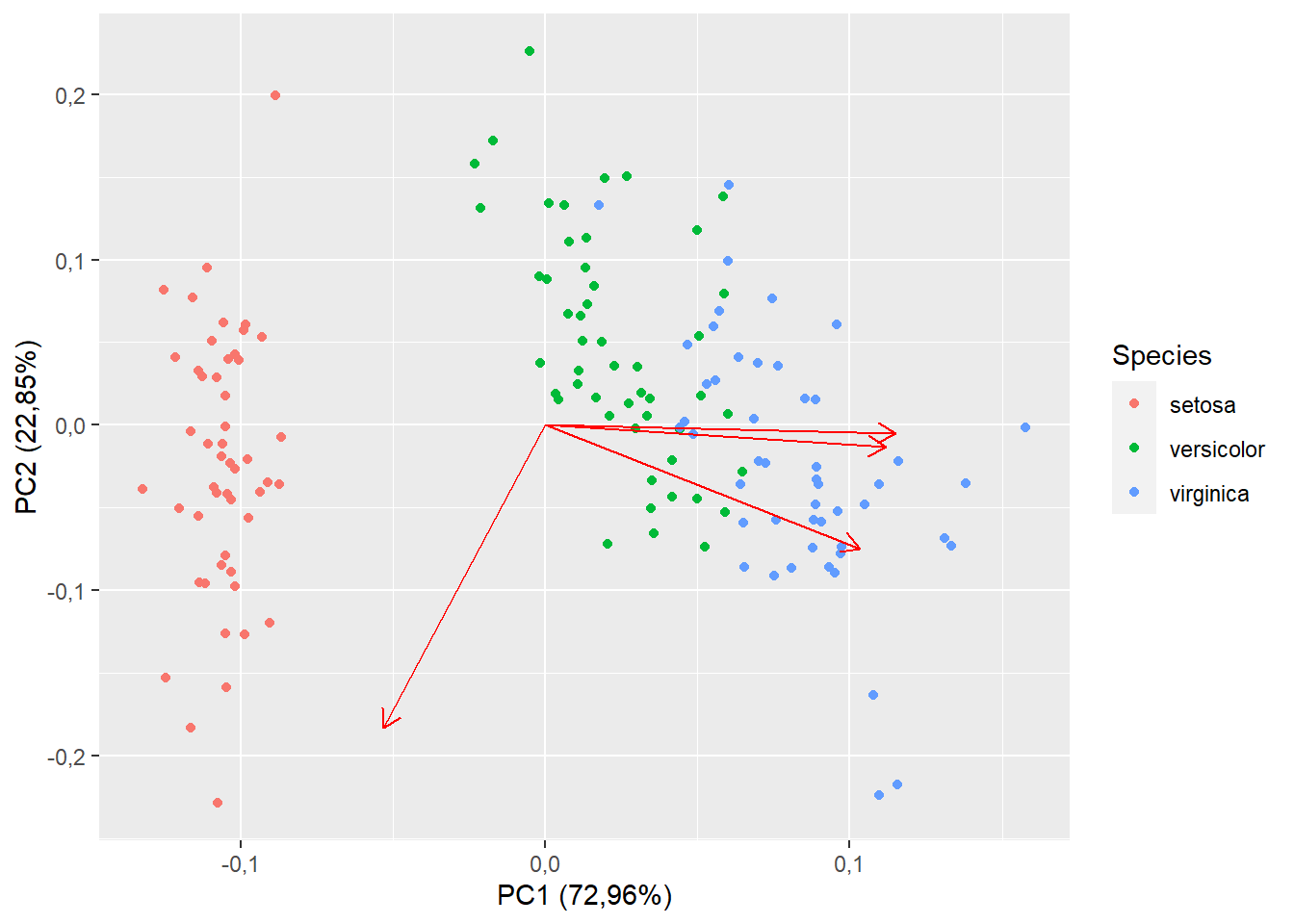
15.1.6 Nome dos vetores
autoplot(pca,
data=iris,
colour="Species",
loadings=T,
loadings.label=T)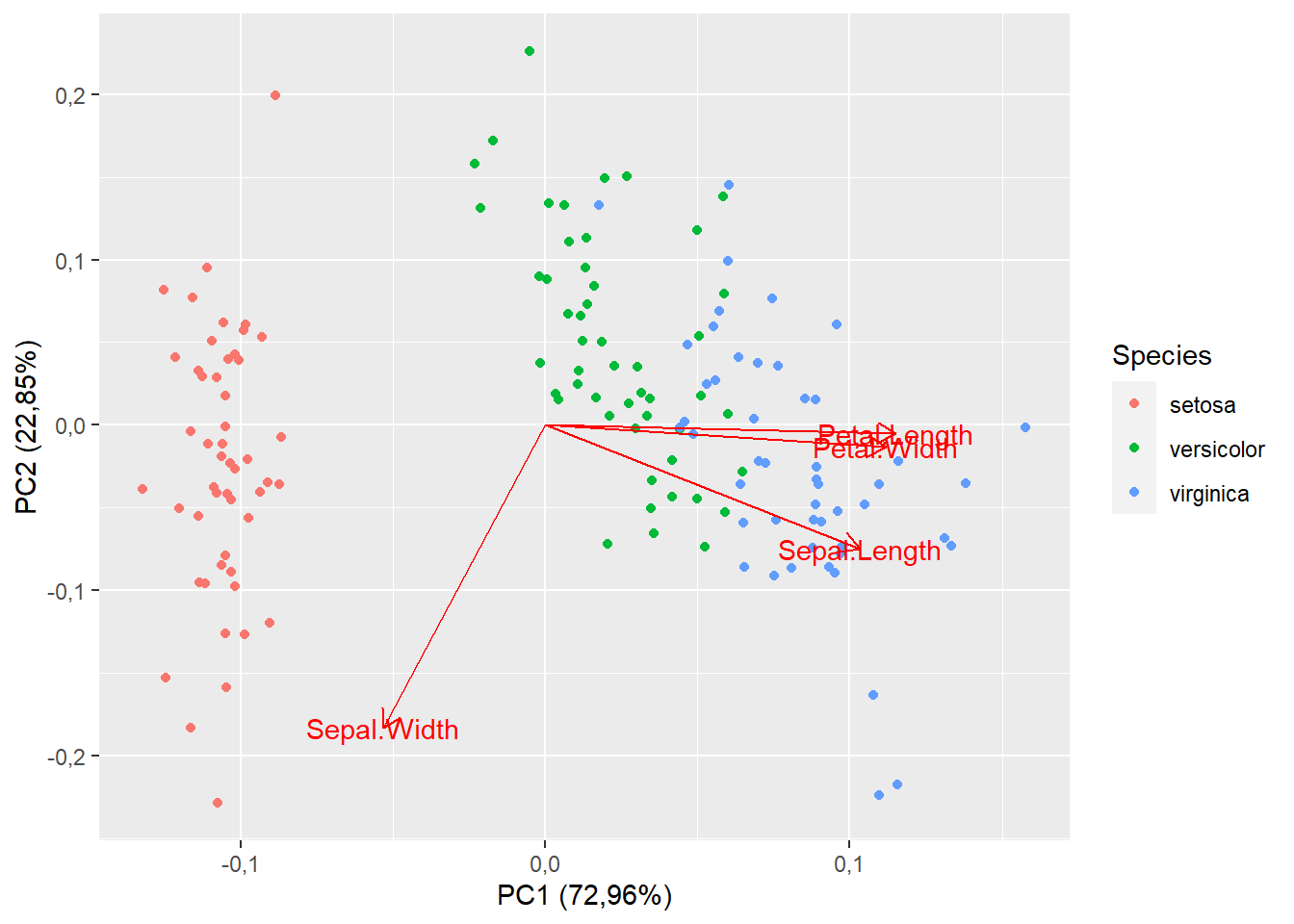
15.1.7 Polígono de agrupamento
autoplot(pca,
data=iris,
colour="Species",
loadings=T,
loadings.label=T,
frame=T)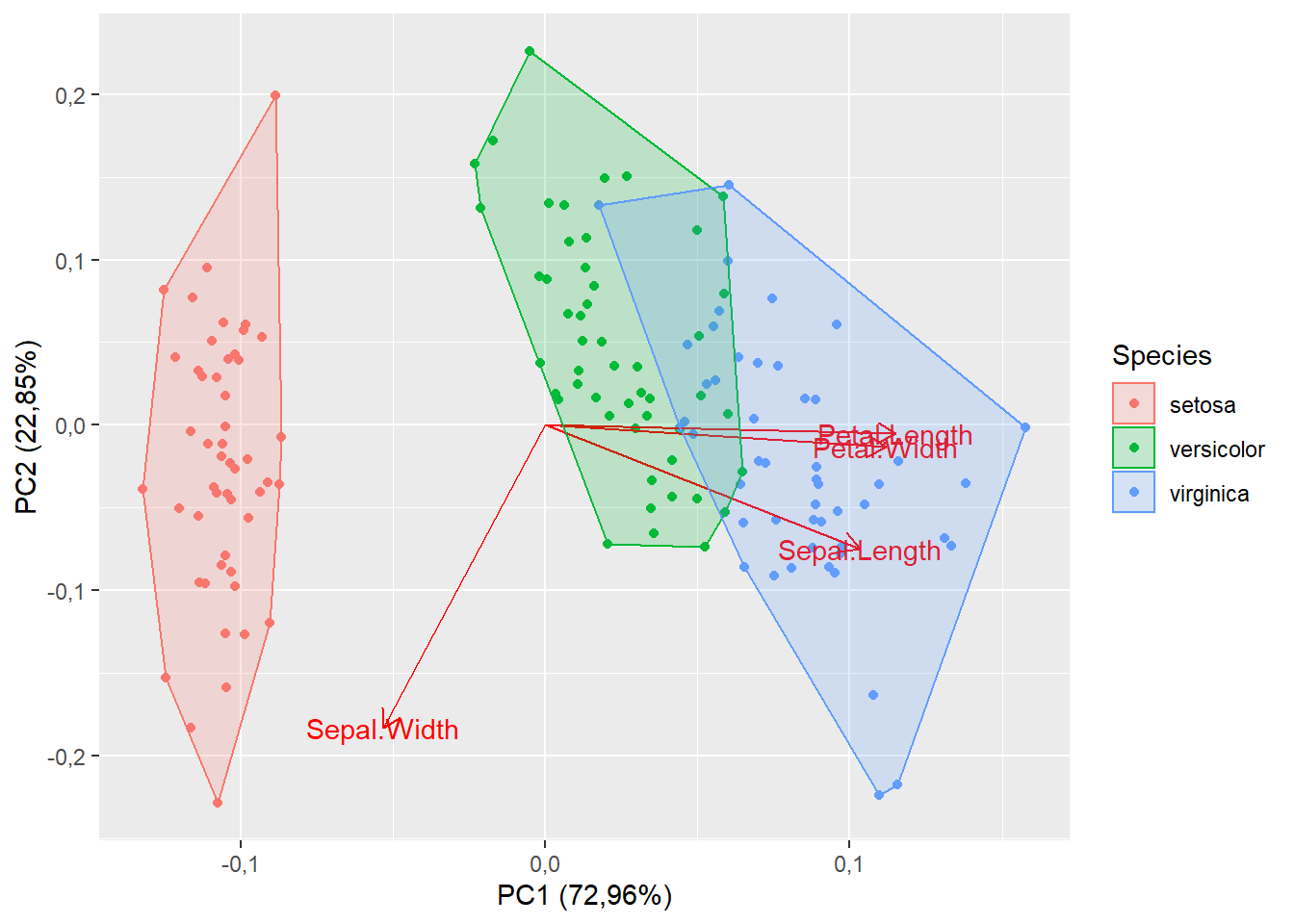
15.1.8 Modificando para elipse
autoplot(pca,
data=iris,
colour="Species",
loadings=T,
loadings.label=T,
frame=T,
frame.type="norm")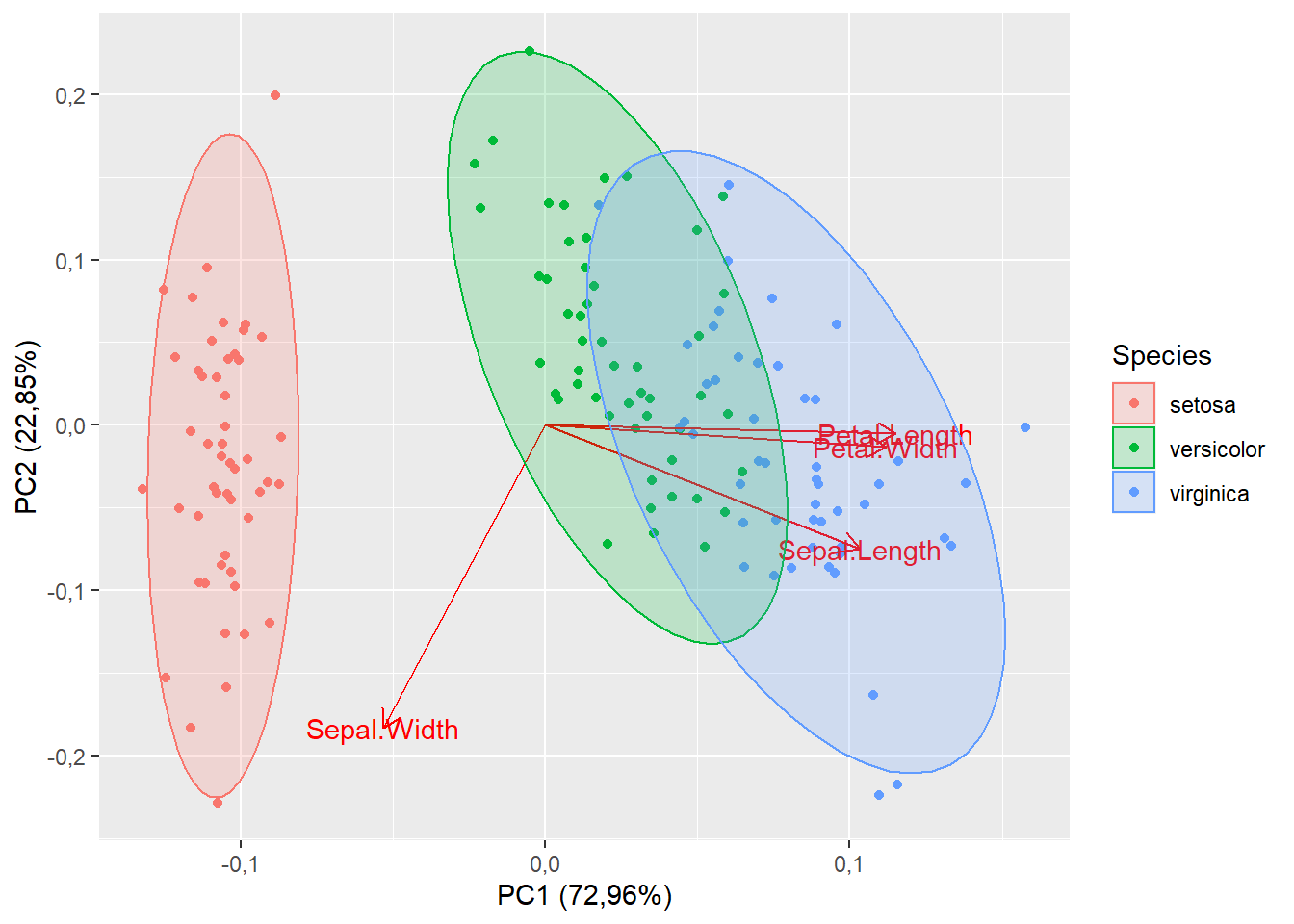
15.1.9 Cor do vetor e do nome
autoplot(pca,
data=iris,
colour="Species",
loadings=T,
loadings.label=T,
frame=T,
frame.type="norm",
loadings.colour="black",
loadings.label.colour="black")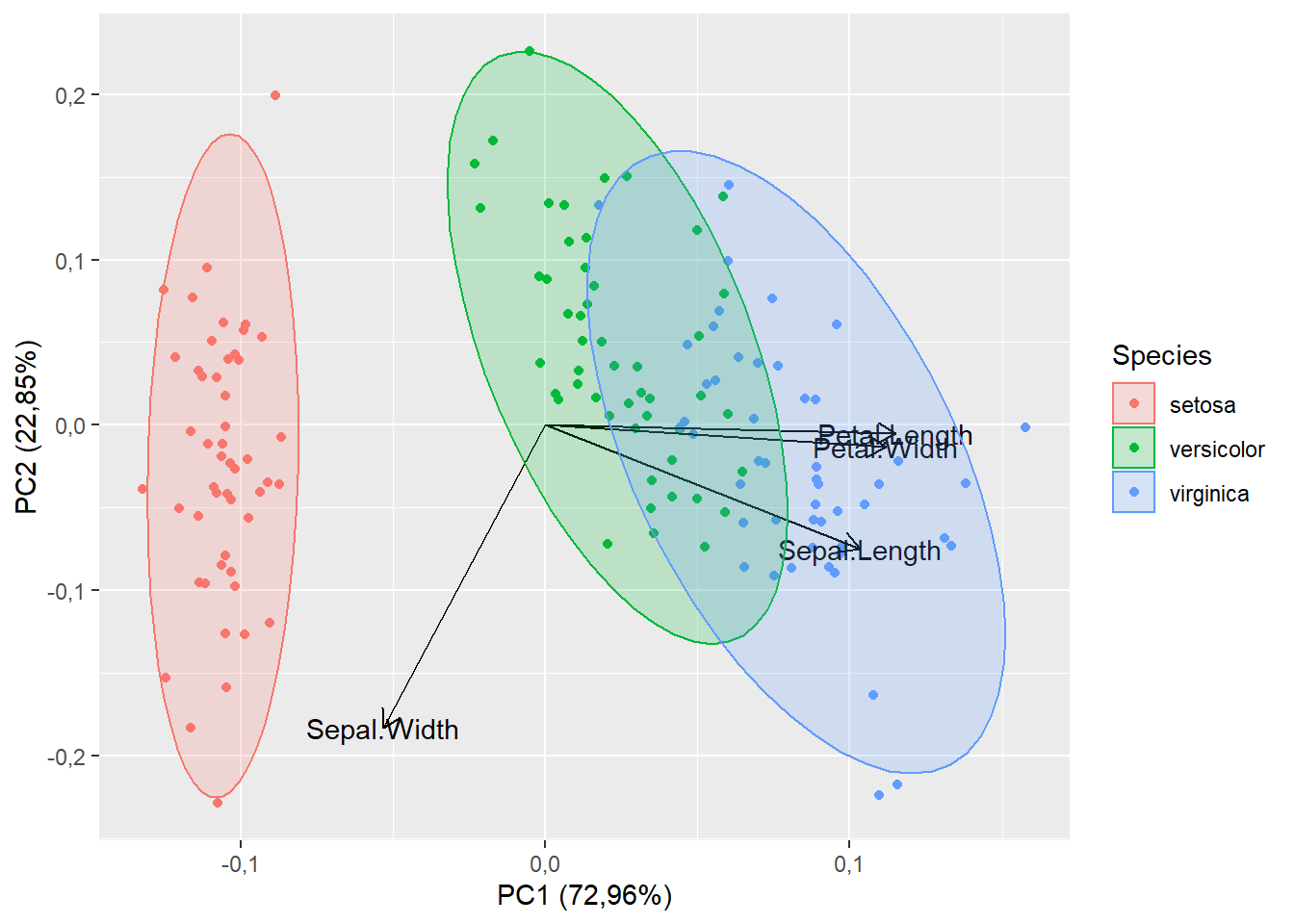
15.1.10 fonte; linha de grade e cor de fundo
autoplot(pca,
data=iris,
colour="Species",
loadings=T,
loadings.label=T,
frame=T,
frame.type="norm",
loadings.colour="black",
loadings.label.colour="black",
loadings.label.family="serif")+theme_bw()+
theme(text = element_text(family="serif"))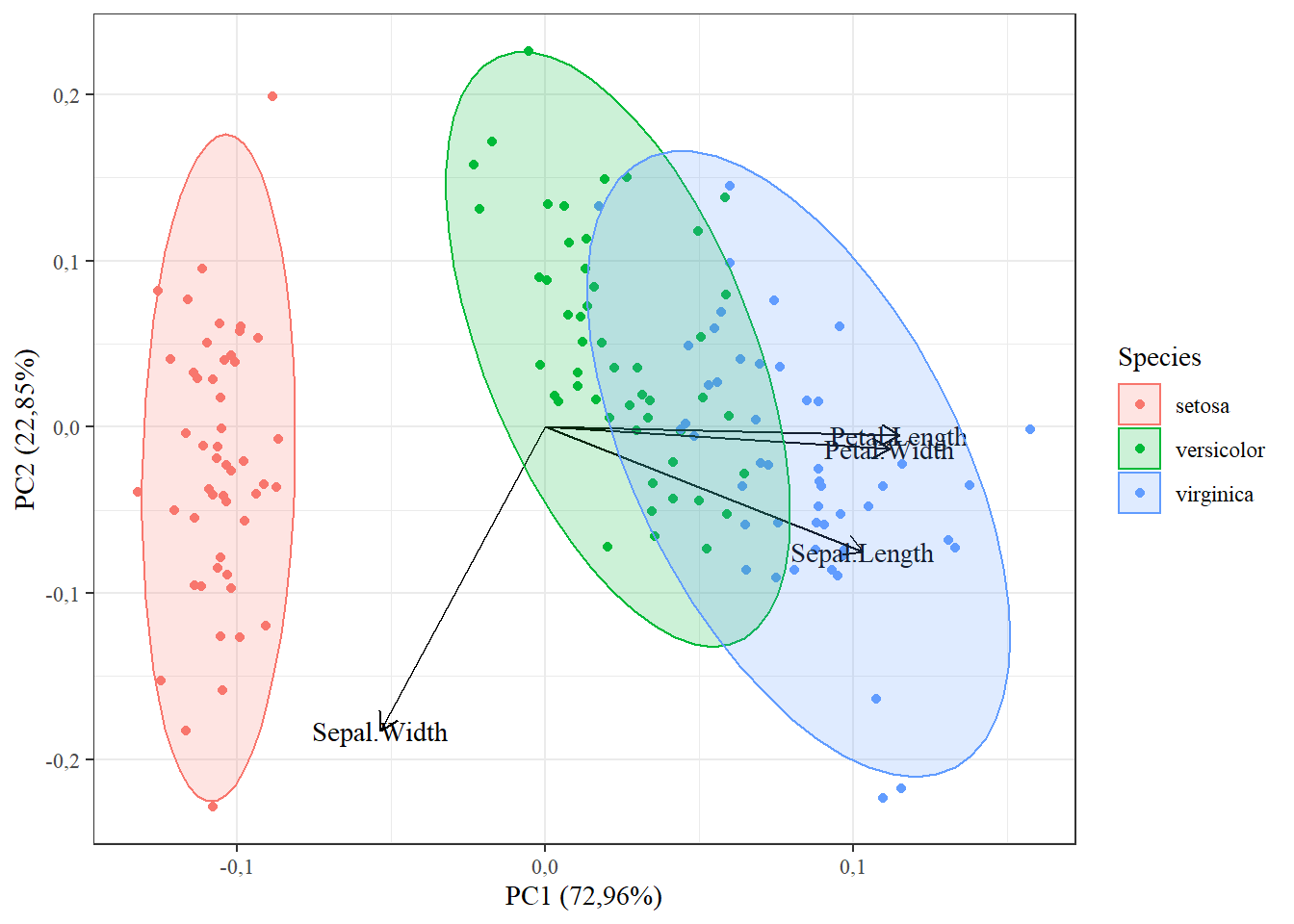
15.1.11 Linha em Y=0 e X=0
autoplot(pca,
data=iris,
colour="Species",
loadings=T,
loadings.label=T,
frame=T,
frame.type="norm",
loadings.colour="black",
loadings.label.colour="black",
loadings.label.family="serif")+theme_bw()+
theme(text = element_text(family="serif"))+
geom_vline(,xintercept = 0,linetype=2)+
geom_hline(,yintercept = 0,linetype=2)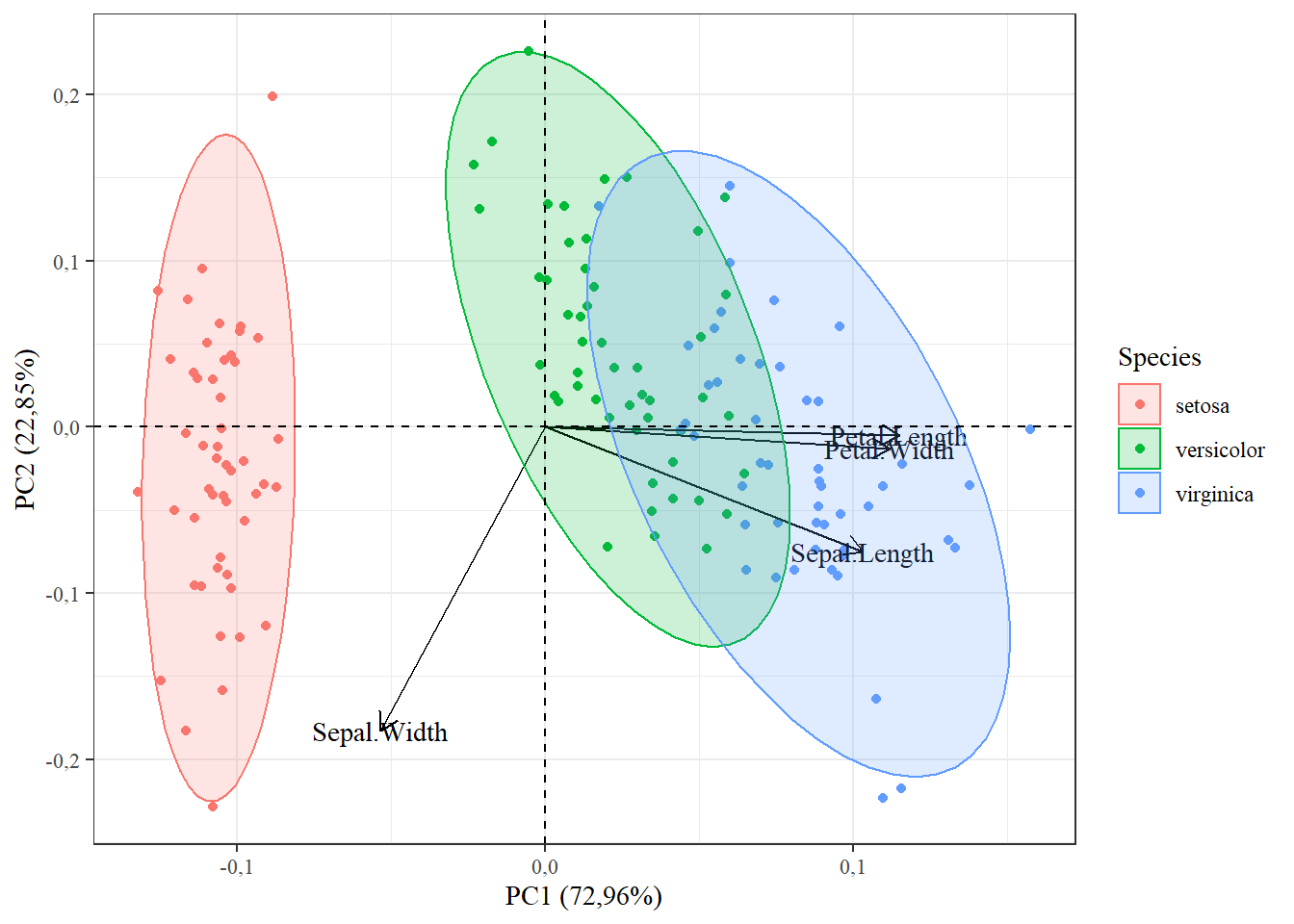
15.2 factoextra e factomineR (Biplot)
rm(list=ls())
DPF=c(46.00,46.00,46.00,46.00,46.00,46.00,43.00,43.00,43.00,46.00,43.00,43.00,46.00,46.00,46.00,49.00,50.00,46.00,43.00,43.00,46.00,43.00,46.00,43.00,39.00,39.00,43.00,43.00,42.00,45.00,43.00,46.00,46.00,43.00,43.00,43.00,43.00,46.00,43.00,49.00,50.00,43.00,39.00,39.00,39.00)
APF=c(58.33,55.00,50.00,41.00,35.67,43.33,35.67,36.00,35.33,46.67,36.67,49.00,38.33,43.67,44.33,41.00,48.00,43.67,32.67,28.67,36.67,38.33,46.33,53.33,38.00,33.00,32.67,45.67,48.33,46.67,33.67,36.67,42.67,37.00,43.67,35.33,42.33,47.00,47.00,59.67,59.00,48.33,32.33,36.33,33.33)
DPM=c(105.00,105.00,102.00,110.00,110.00,112.00,110.00,110.00,105.00,112.00,112.00,110.00,110.00,112.00,112.00,112.00,112.00,112.00,110.00,105.00,105.00,110.00,102.00,102.00,110.00,105.00,110.00,110.00,110.00,104.00,105.00,105.00,104.00,104.00,104.00,102.00,104.00,105.00,102.00,110.00,112.00,112.00,102.00,102.00,102.00)
APM=c(100.00,90.33,97.00,91.33,97.67,77.33,90.00,93.00,91.33,98.00,84.67,91.33,92.33,101.67,102.33,102.33,98.33,93.00,78.67,72.33,72.33,97.67,104.33,96.00,99.00,97.00,94.33,104.67,115.00,117.67,81.33,82.33,83.00,104.33,107.33,103.00,89.33,90.33,82.33,123.33,115.00,133.33,60.00,59.00,65.67)
IPV=c(15.00,20.00,17.00,10.00,22.67,14.33,23.00,19.33,15.33,14.33,15.00,22.67,14.67,15.33,17.00,13.67,16.67,19.33,11.00,8.67,11.33,13.00,14.67,13.00,13.00,12.00,17.67,14.67,10.67,25.00,18.00,14.00,18.67,15.67,11.00,18.00,16.33,24.33,17.00,13.33,11.00,22.33,10.33,5.67,14.00)
ACA=c(2.00,1.90,2.20,1.50,1.20,1.00,2.00,1.50,1.20,3.00,1.40,1.60,1.80,2.50,2.50,2.00,1.70,1.80,1.50,2.00,1.50,1.80,2.00,1.80,1.30,1.20,2.00,3.00,2.00,3.00,1.50,1.80,2.20,1.80,1.80,2.00,1.80,3.50,3.50,1.50,2.50,2.00,1.20,1.00,1.20)
PRO=c(2444.44,2870.37,2314.81,2629.63,2444.44,2592.59,2962.96,3037.04,3037.04,2592.59,2296.30,2444.44,2370.37,3481.48,2555.56,1981.48,2611.11,1925.93,1870.37,2518.52,2370.37,2462.96,2351.85,2000.00,2703.70,2685.19,2166.67,2129.63,2222.22,1814.81,2537.04,2351.85,2333.33,3370.37,2462.96,3129.63,2666.67,2796.30,2055.56,2333.33,2240.74,2092.59,2703.70,2129.63,2740.74)
MCG=c(10.78,10.96,10.07,10.77,11.17,11.24,12.57,13.35,13.77,14.23,13.61,13.30,11.85,11.80,12.04,10.10,10.19,9.97,12.15,11.35,11.70,12.83,11.52,11.10,10.95,11.14,10.26,12.51,11.87,12.30,14.20,13.13,14.70,13.08,12.76,13.74,14.59,13.98,13.52,12.72,12.22,12.63,10.93,10.65,10.67)
Tratamento=rep(c(paste("T",1:5)),9)
dados=data.frame(Tratamento,DPF,APF,DPM,APM,IPV,ACA,PRO,MCG)15.2.1 Valores dos CP
require(FactoMineR)
pca=PCA(dados[c(2,3,4,5,6,7,9)],scale.unit=T,graph=F)
round(pca$eig,3)## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 2,648 37,821 37,821
## comp 2 1,411 20,152 57,974
## comp 3 0,939 13,418 71,392
## comp 4 0,650 9,282 80,673
## comp 5 0,608 8,692 89,365
## comp 6 0,479 6,842 96,207
## comp 7 0,266 3,793 100,00015.2.2 Gráfico básico
require(factoextra)
fviz_pca_biplot(pca,geom = c("point"))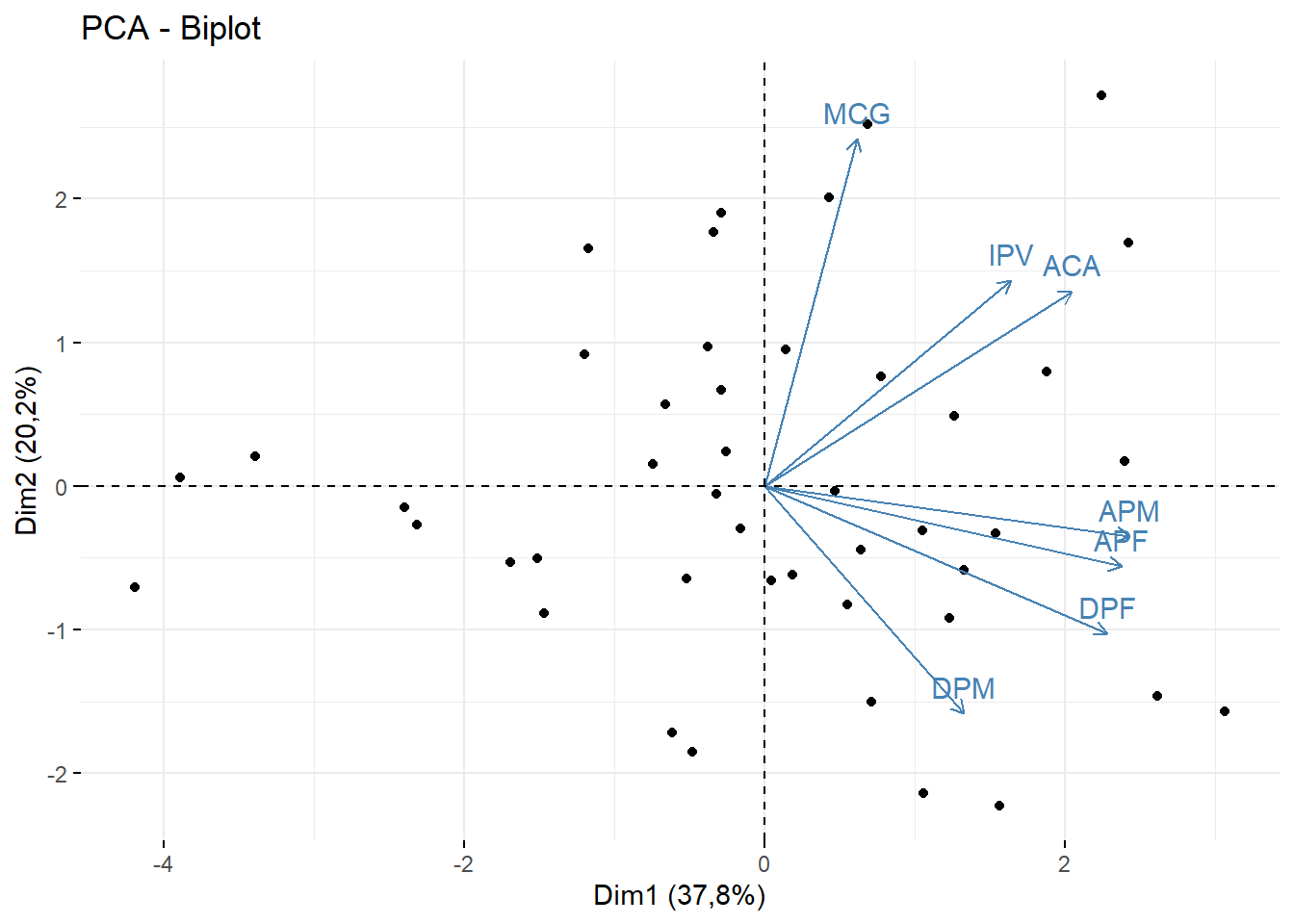
15.2.3 Elipse geral
require(factoextra)
fviz_pca_biplot(pca,geom = c("point"),
addEllipses = T)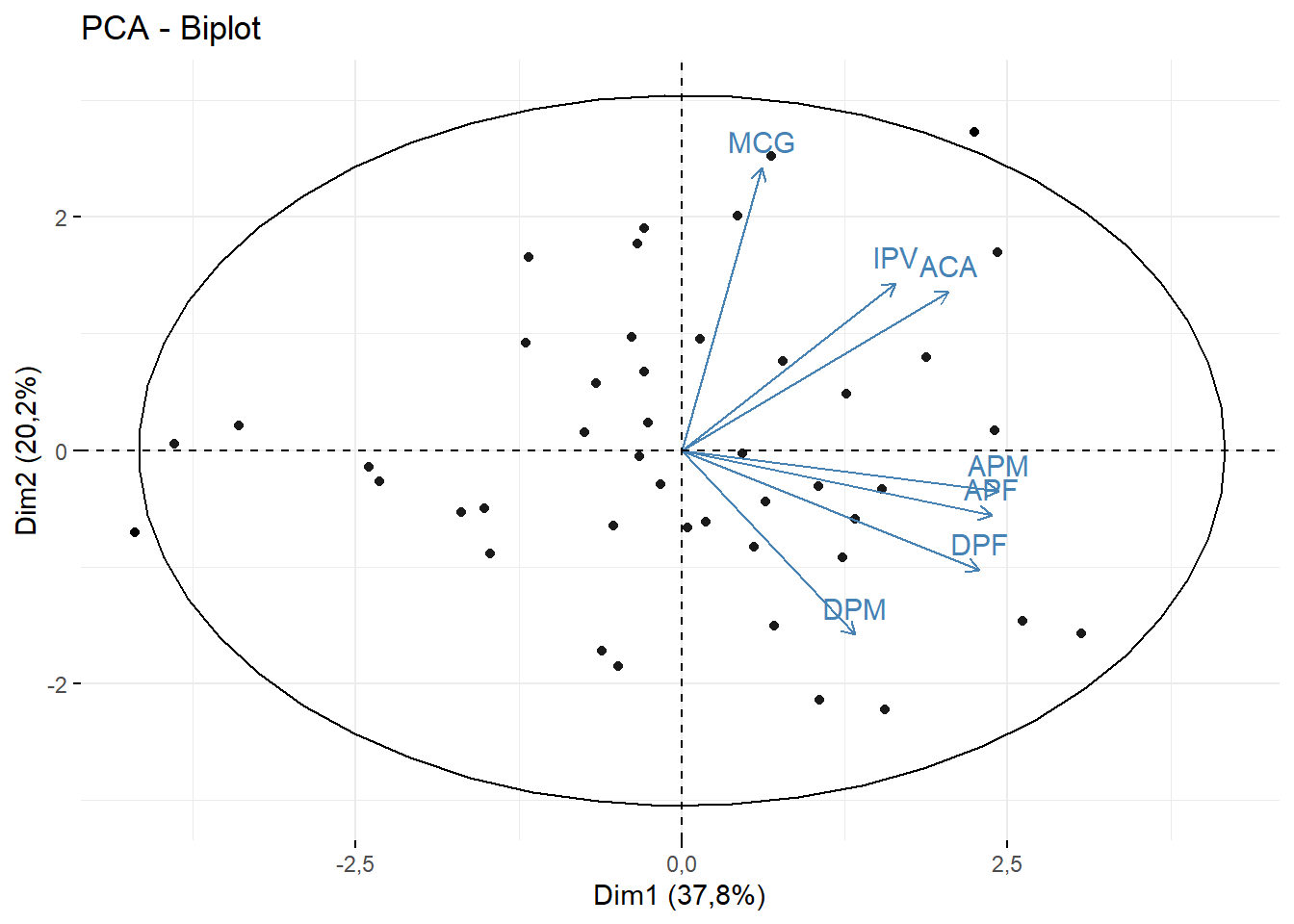
15.2.4 Elipse por Tratamentos
require(factoextra)
fviz_pca_biplot(pca,geom = c("point"),
addEllipses = T, fill.ind = dados$Tratamento)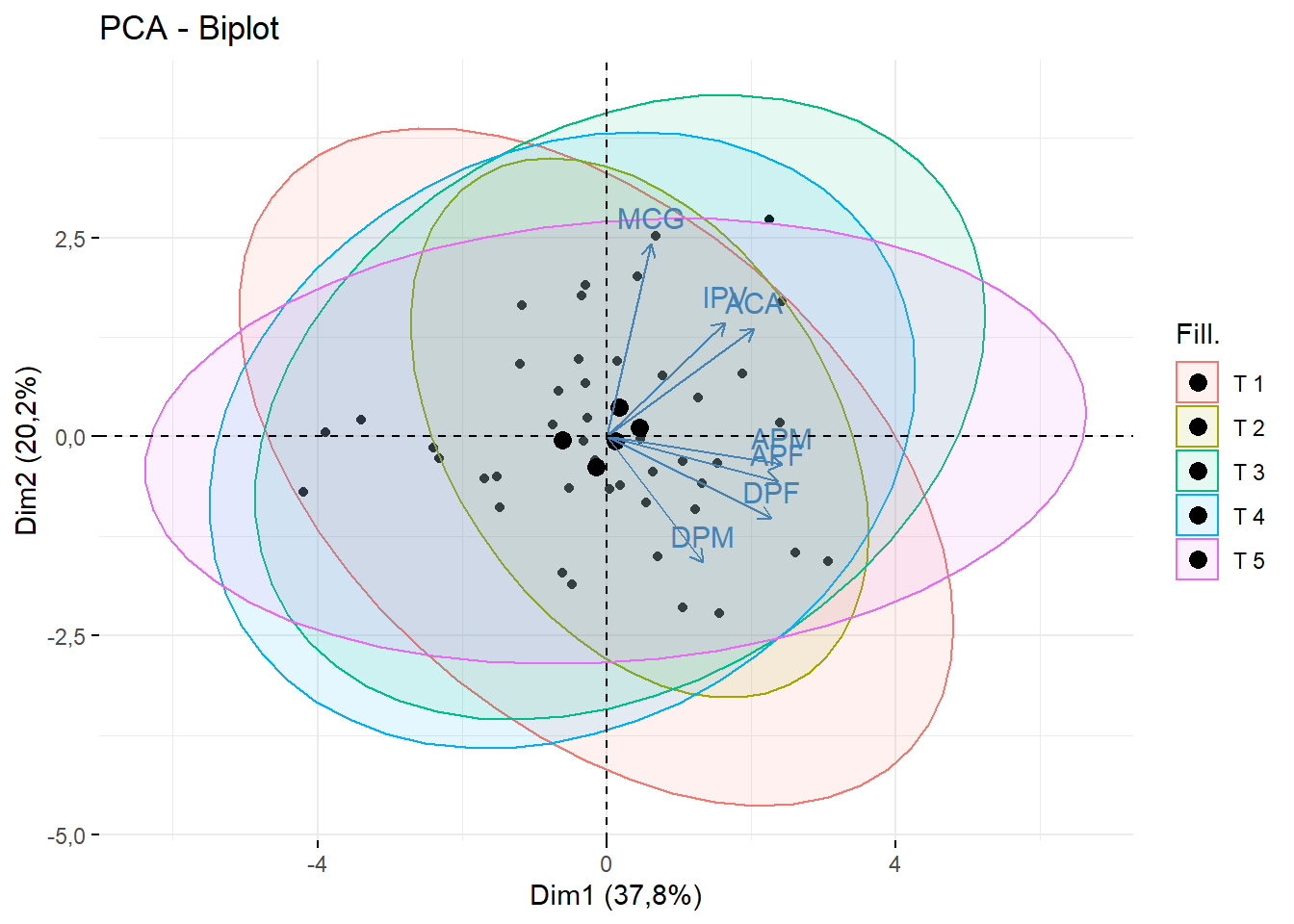
15.2.5 Removendo título
require(factoextra)
fviz_pca_biplot(pca,geom = c("point"),
addEllipses = T,
fill.ind = dados$Tratamento,
title = "")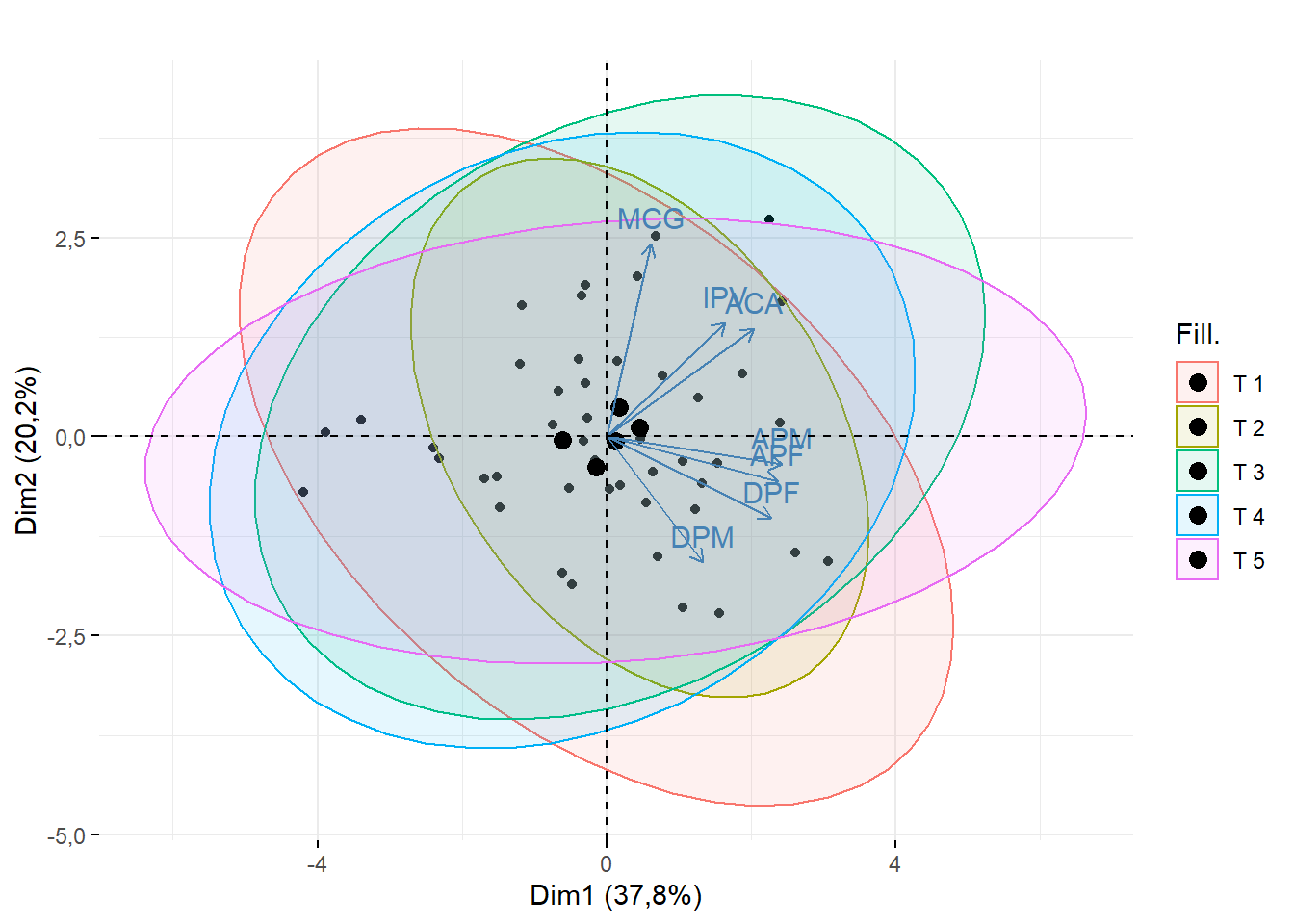
15.2.6 Sobreposição de legendas
require(factoextra)
fviz_pca_biplot(pca,geom = c("point"),
addEllipses = T, ## adicionar elipse
fill.ind = dados$Tratamento,
title = "",
repel=T)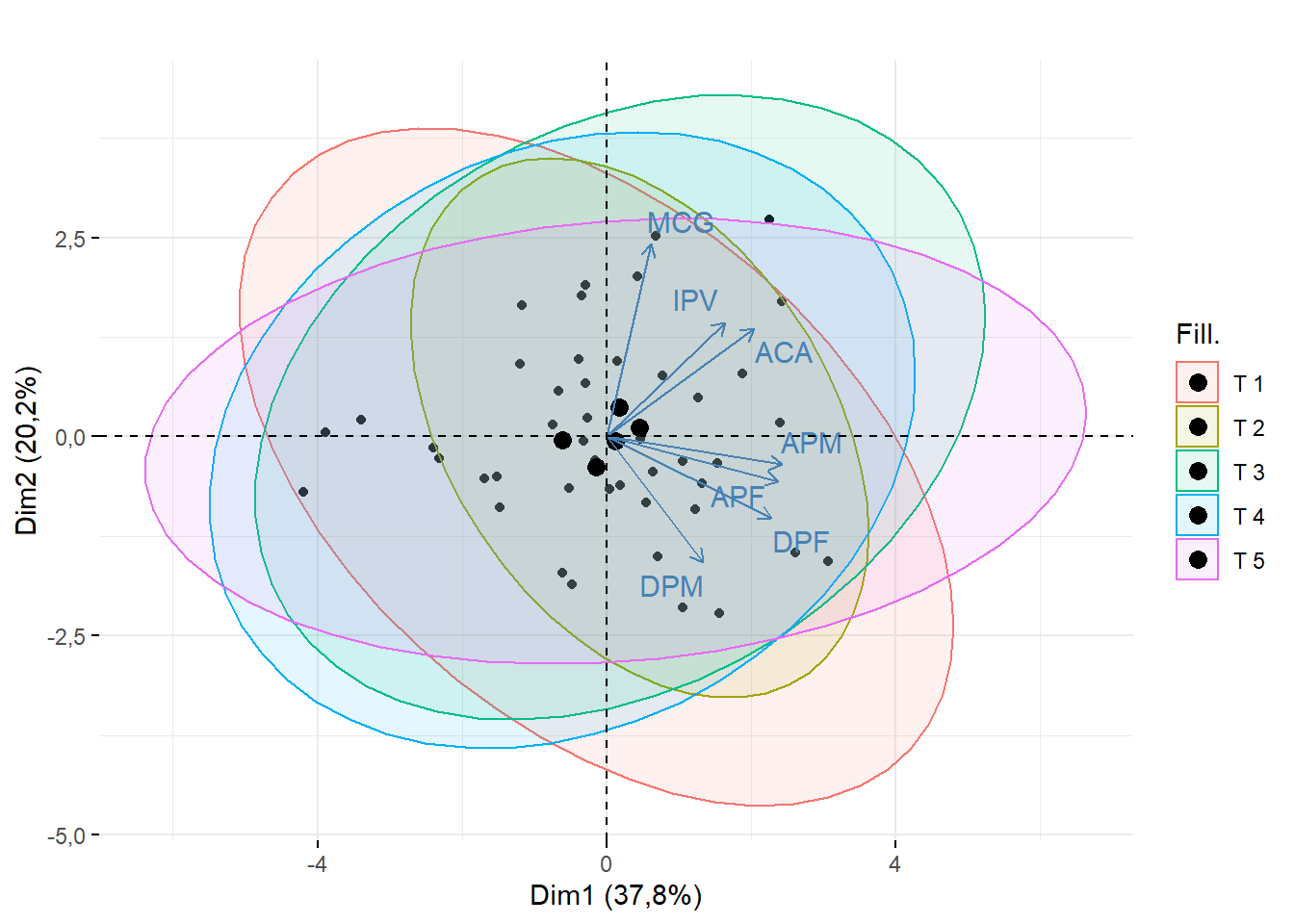
15.2.7 Tamanho do ponto, letra e a cor
require(factoextra)
fviz_pca_biplot(pca,geom = c("point"),
addEllipses = T,
fill.ind = dados$Tratamento,
title = "",
repel=T,
pointshape=21,pointsize=2,textsize=0.5, col.var="black")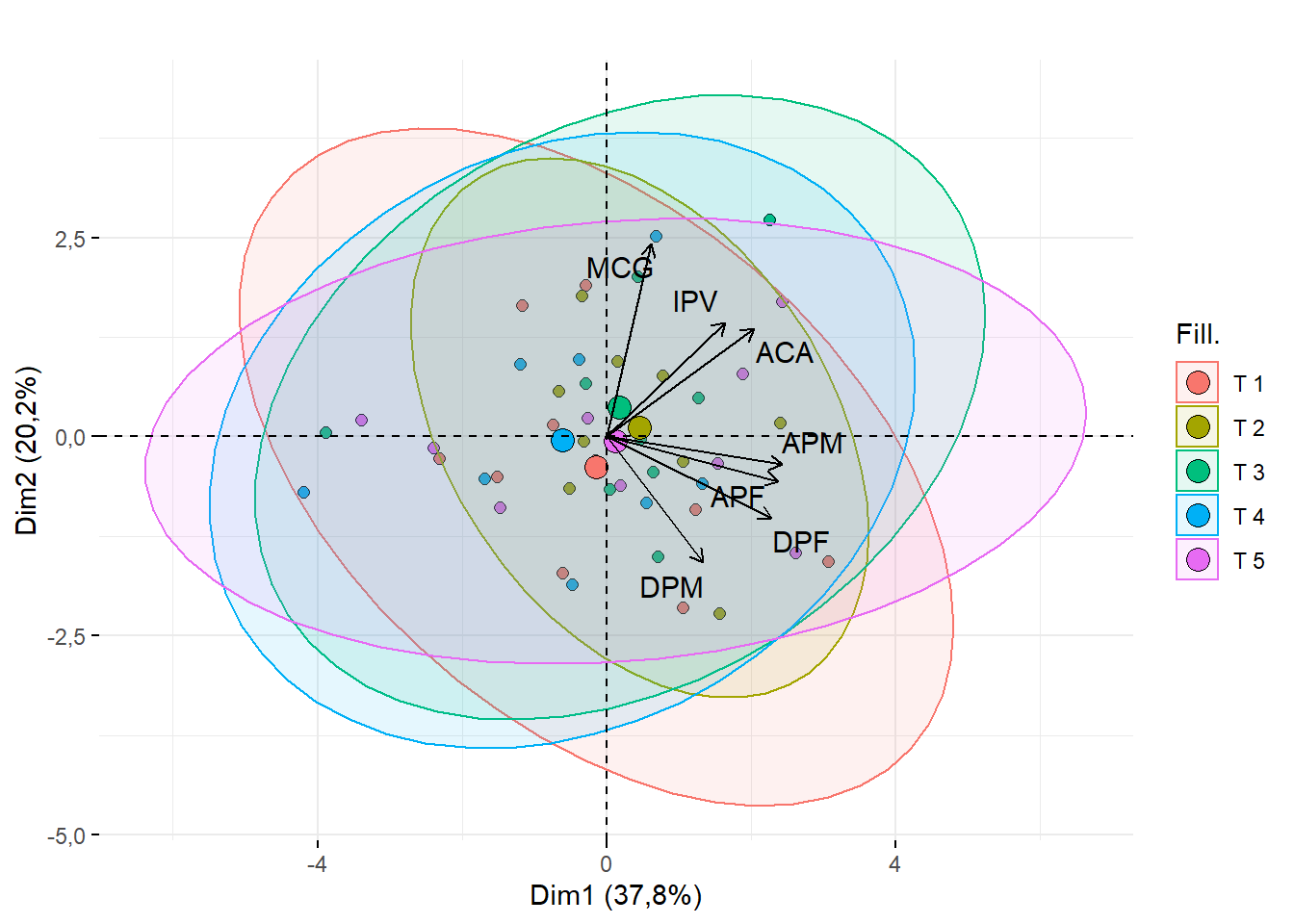
15.2.8 Título das ellipses
require(factoextra)
fviz_pca_biplot(pca,geom = c("point"),
addEllipses = T,
fill.ind = dados$Tratamento,
title = "",
repel=T,
pointshape=21,pointsize=2,textsize=0.5, col.var="black",fill= "Cultivares")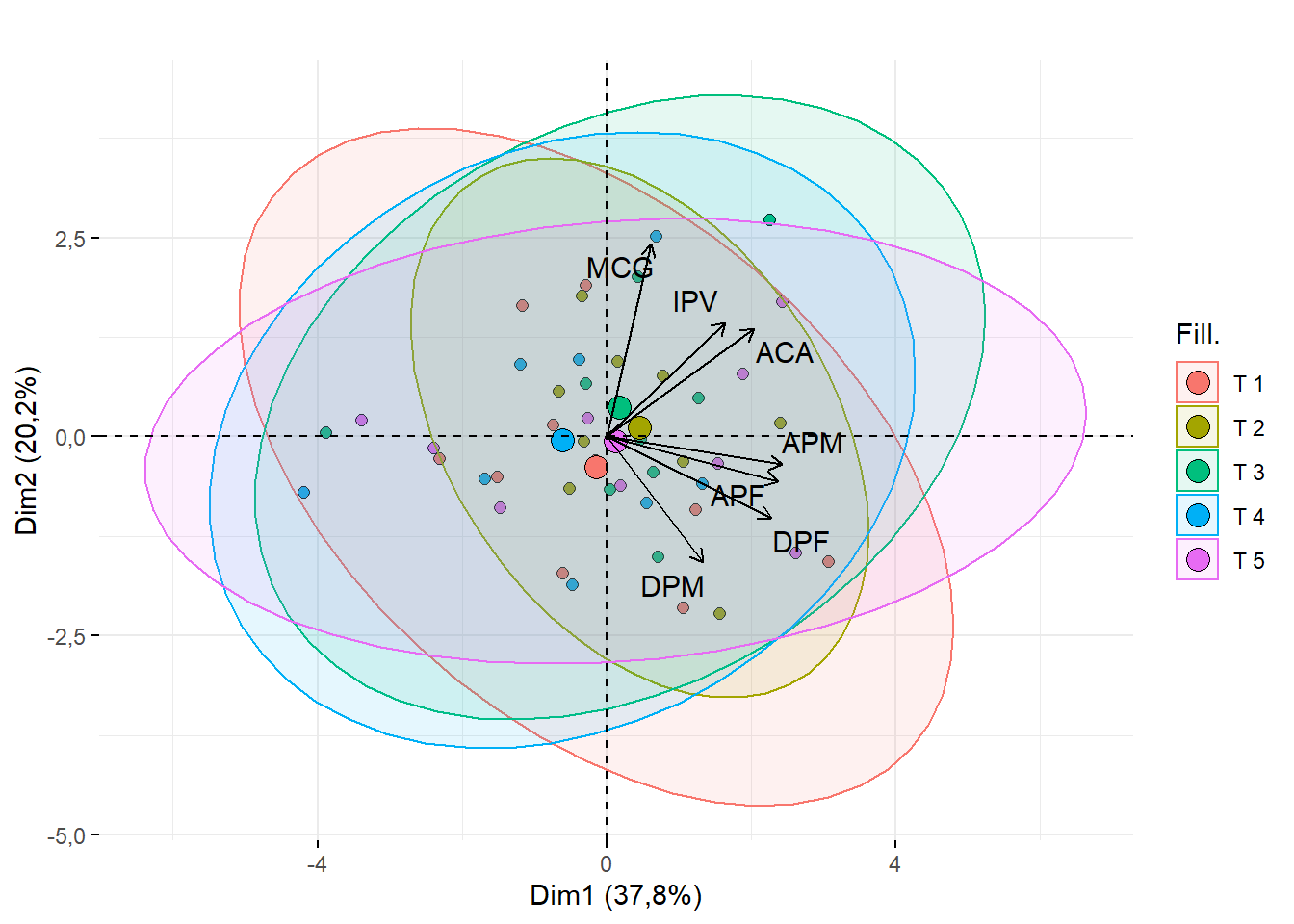
15.2.9 Título do 1 e 2 CP
require(factoextra)
fviz_pca_biplot(pca,geom = c("point"),
addEllipses = T,
fill.ind = dados$Tratamento,
title = "",
repel=T,
pointshape=21,pointsize=2,textsize=0.5,
col.var="black",fill= "Cultivares")+ylab("CP2(20,2%)")+xlab("CP1(37,8%)")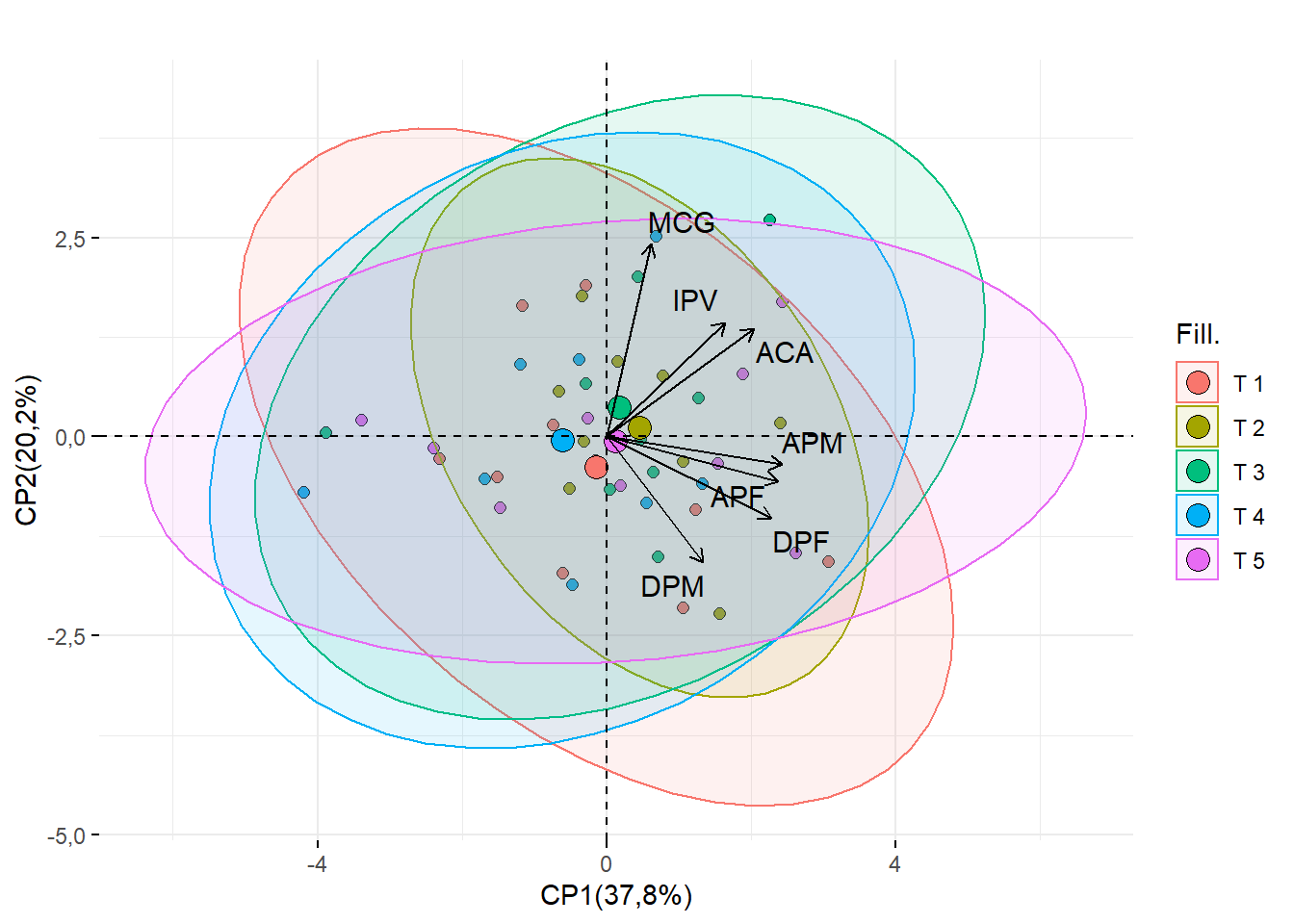
15.3 factoextra (Gráficos separados)
15.3.1 Conjunto de dados
ph=c(5.4,6.7,6.8,5.9,6.3,6.2,6.3,6,6.1,5.8,6.7,5.7,6.8,6.9,6.5,6.9,6.8,6.7,6.5,6.5,6.7,6.7,6.5,6.7,6.6,6.8,6.4,4.6,6.5,6.6,6.3,6.2,5.5,4.5,5.2,6.5,6.3,6.6,6.4,6.6,6.6,6.5,6.5,6.4,6.5,6.8,6.7,6.6,5.9,6.1,6.3,6.3,6.2,5.3,5.8,6.1,6.7,6.7,6.6,6.6,6.6,6.8,6.8,6.7,6.9,7,7.1,7.1,6.7,6.7,6.6,6.6,6.3,5.8,6.2,6.3,6,5,6.3,5.3,5.4,6.4,6.7,6.5,6.5,6.4,6.7,6.5,6.8,6.2,6.1,6.2,6.8,6.7,6.6,6.4,6.7,6.6,6.4,5.9,6.5,6.6,5.9,6.8,6.8,6.7,6.5,6.7,6.9,6.5,6.8,6.7,6.8,6.6,6.7,6.7,6.9,6.9,6.7,6.8)
HAL=c(4.6,2.7,2.7,3.9,3.4,3.6,3.4,3.9,3.6,3.9,2.5,4.2,2.5,2.5,3.1,2.5,2.5,2.9,3.1,3.1,2.7,2.9,2.9,2.9,3.1,2.7,3.4,8.3,2.9,2.9,3.6,3.1,4.9,8.3,5.3,3.1,2.7,2.7,2.7,2.7,3.1,3.1,2.7,3.1,2.5,2.5,2.9,2.9,3.9,3.9,3.6,3.4,3.9,5.3,3.9,3.9,2.9,2.7,2.9,3.1,2.7,2.1,2.3,2.3,2.3,2.1,2.0,2.1,2.5,2.3,2.5,2.5,3.1,3.6,2.9,2.9,3.4,4.9,2.5,4.6,4.2,2.5,2.3,2.5,2.7,2.5,2.1,2.5,2.1,2.9,2.9,2.9,2.1,2.3,2.5,2.7,2.5,2.5,2.7,3.6,2.7,2.5,3.4,2.0,2.3,2.3,2.7,2.3,2.1,2.5,2.1,2.3,2.3,2.5,2.5,2.3,2.1,2.3,2.3,2.1)
K=c(0.5,0.7,0.7,0.9,0.9,0.8,0.6,0.9,0.8,0.6,0.5,0.4,2.0,1.9,1.0,1.2,1.2,1.6,1.5,0.9,2.0,1.2,1.6,1.4,0.9,0.8,0.8,1.0,0.9,1.1,1.2,1.1,0.6,0.5,0.6,0.9,1.4,1.6,1.3,1.5,0.9,1.2,1.3,1.0,1.4,0.7,0.7,1.0,1.0,0.7,0.8,1.3,0.7,0.7,0.8,0.8,1.3,0.9,1.2,0.8,1.5,1.4,0.8,1.0,1.4,1.1,1.6,1.0,0.9,1.1,1.1,0.9,1.0,0.7,0.6,1.0,1.0,0.7,1.0,0.6,0.9,1.2,0.8,0.8,0.8,0.7,1.1,1.2,0.8,0.9,0.9,1.2,1.1,1.1,1.2,0.9,0.8,0.7,0.9,0.7,0.8,0.9,0.5,0.8,1.0,0.7,0.8,0.7,1.4,0.9,1.4,0.9,1.0,1.3,0.7,1.3,1.4,0.9,0.8,1.4)
P=c(13.7,14.5,65.7,20.5,20.7,19.3,16.2,14.6,15.8,8.7,8.9,7.7,20.0,18.4,9.4,14.8,17.5,11.7,11.2,11.1,51.4,20.4,27.3,14.1,20.1,18.1,23.5,36.4,16.9,18.6,29.0,20.9,16.8,16.8,8.6,11.3,17.5,17.0,30.9,17.2,10.7,17.2,10.9,14.5,26.6,42.1,10.5,13.5,16.4,13.3,34.7,20.0,12.8,15.1,15.8,14.1,26.9,33.2,25.4,25.1,14.1,17.7,12.6,12.9,27.5,18.6,16.9,15.5,16.2,17.6,17.5,14.5,12.6,10.5,10.6,10.5,14.7,10.1,10.7,9.6,17.9,23.9,22.4,22.0,14.2,15.8,12.8,17.8,16.0,10.5,9.6,13.8,17.5,17.7,10.0,10.1,29.0,16.8,18.6,31.7,17.2,40.2,9.8,14.5,28.8,13.0,13.1,18.6,22.0,36.0,19.5,25.2,14.2,15.8,11.9,16.7,20.0,14.7,11.7,17.9)
Ca=c(3.43,4.24,5.37,4.13,4.48,4.65,4.33,4.19,3.91,3.23,4.01,2.98,4.55,4.53,3.91,4.33,4.62,4.54,3.38,3.87,3.85,3.91,3.79,4.57,4.71,4.75,4.93,4.32,4.08,3.73,3.30,3.88,2.59,1.99,2.27,3.68,4.94,5.29,5.69,5.67,4.55,5.01,4.85,4.76,4.99,5.13,4.40,4.38,3.05,3.78,4.21,4.22,3.55,2.81,2.98,3.35,4.03,3.80,3.88,3.97,4.32,4.81,5.06,4.98,5.46,4.88,5.37,5.36,5.41,5.05,5.22,4.95,6.06,3.51,3.72,3.25,2.74,1.78,2.86,2.31,3.63,4.91,4.47,4.85,4.78,6.76,4.31,4.62,4.54,3.10,2.88,3.66,5.56,5.08,4.89,4.67,5.71,5.47,4.68,4.72,4.45,4.23,3.36,4.27,4.31,3.48,3.42,4.38,5.37,7.21,5.40,5.71,4.53,4.35,3.87,3.68,4.18,4.95,4.40,4.84)
Mg=c(2.24,3.22,3.20,2.46,2.51,2.65,2.84,2.80,2.56,2.56,3.45,2.43,3.17,3.25,2.89,3.30,3.34,3.28,2.91,3.00,3.29,2.83,2.89,2.86,2.82,3.15,2.49,2.65,2.95,3.20,2.88,3.10,2.28,1.92,2.05,3.18,3.19,3.13,3.35,3.44,3.27,3.18,3.35,3.24,3.29,3.37,3.21,3.19,2.50,2.01,2.61,2.74,2.42,2.05,2.29,2.36,3.33,3.30,3.03,2.90,2.99,3.34,3.33,3.35,3.30,3.10,3.47,3.30,3.30,3.23,3.25,3.23,3.49,2.40,2.70,2.83,2.78,1.98,2.89,2.30,2.35,3.20,3.45,2.74,2.97,4.56,3.28,2.80,3.03,2.79,2.68,2.95,3.43,3.38,3.30,3.13,3.25,3.06,2.99,2.49,2.84,2.81, 2.22,3.48,3.08,2.80,2.62,2.79,3.30,3.39,3.23,3.14,3.31,2.94,3.03,3.17,2.98,3.38,3.13,3.21)
V=c(57.27,75.06,77.30,65.31,69.75,68.82,69.49,66.52,66.47,61.75,75.94,57.72,79.32,79.29,71.24,77.71,78.33,76.18,71.19,71.14,76.94,72.96,73.78,75.10,72.70,76.02,70.72,48.85,73.04,73.25,66.68,71.78,52.34,34.52,48.24,70.98,77.75,78.59,79.11,79.57,73.40,74.76,77.59,73.97,79.17,78.45,73.85,74.40,62.52,62.12,67.51,70.86,62.69,51.35,60.67,62.34,74.62,74.63,73.41,70.85,76.35,81.43,79.59,79.78,81.17,80.69,83.74,81.62,79.09,79.87,79.09,78.23,76.80,64.16,70.53,70.54,65.82,47.34,72.73,53.10,61.80,78.52,78.78,76.85,75.73,82.58,80.00,77.24,79.24,69.95,68.90,72.68,82.19,80.29,78.75,76.06,79.42,78.49,75.87,68.39,74.74,75.88,64.04,80.92,78.00,74.94,71.55,76.95,82.11,81.94,82.16,80.58,78.89,77.11,75.13,77.63,79.68,79.73,77.91,81.24)
Trat=rep(c(paste("T",1:10)), e=12)
dados=data.frame(Trat,ph,HAL,K,P,Ca,Mg,V)15.3.2 Calculando as médias
mph=tapply(ph, Trat, mean)
mHAL=tapply(HAL, Trat, mean)
mK=tapply(K, Trat, mean)
mP=tapply(P, Trat, mean)
mCa=tapply(Ca, Trat, mean)
mMg=tapply(Mg, Trat, mean)
mV=tapply(V, Trat, mean)
dadosm=data.frame(mph,mHAL,mK,mP,mCa,mMg,mV)15.3.3 Dendrograma (Definir Clusters)
dend=as.dendrogram(hclust(dist(dadosm), method='average'), hang = -1)
plot(dend)
abline(h=8, lty=2, col="red")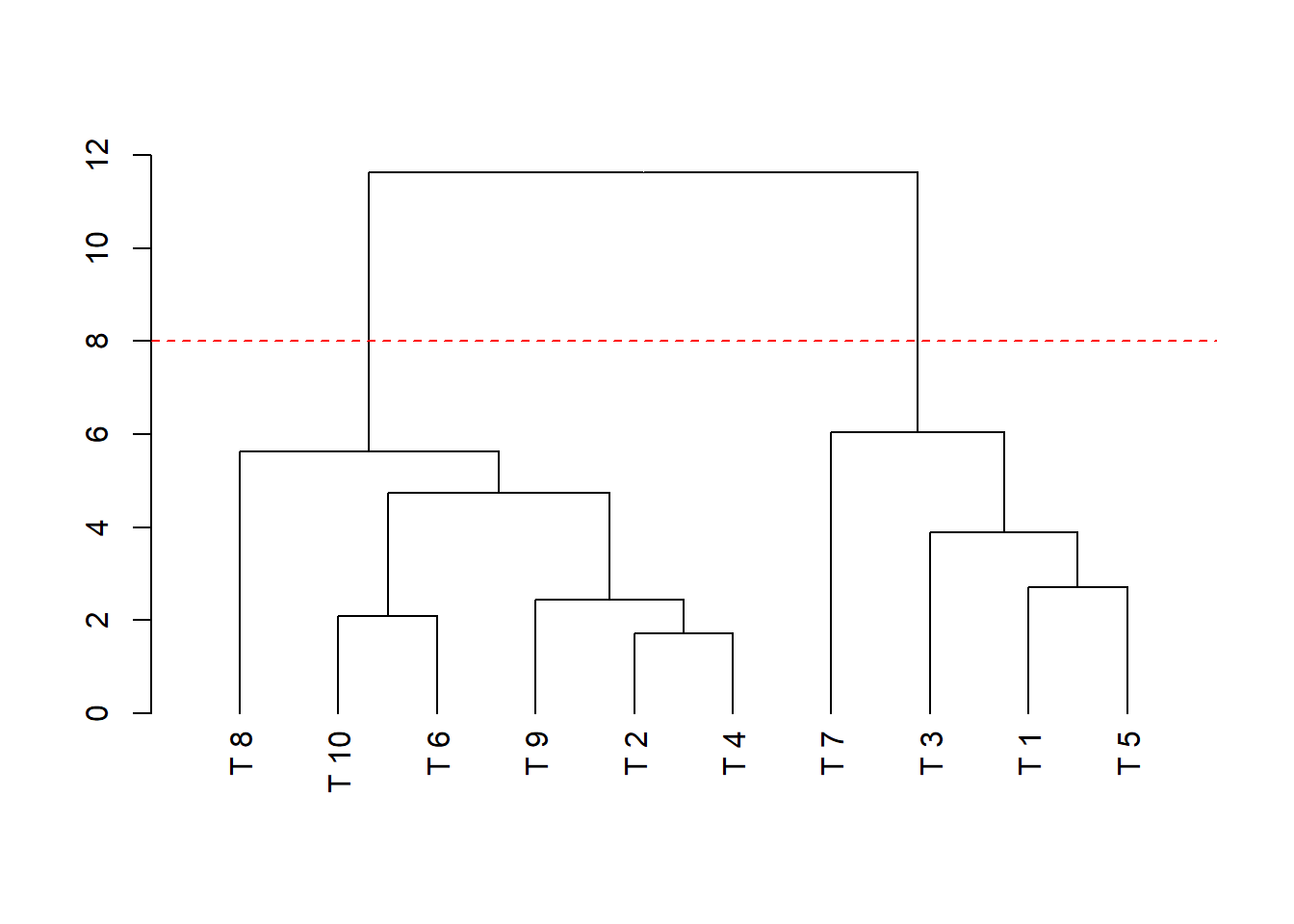
## Cluster 1: T8, T10, T6,T9,T2,T4
## Cluster 2: T7, T3, T1, T515.3.4 Valores dos CP
require(FactoMineR)
pca=PCA(dadosm,scale.unit=T,graph=F)
round(pca$eig,3)## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 5,057 72,243 72,243
## comp 2 1,037 14,812 87,055
## comp 3 0,639 9,128 96,183
## comp 4 0,237 3,387 99,571
## comp 5 0,022 0,312 99,883
## comp 6 0,008 0,109 99,992
## comp 7 0,001 0,008 100,00015.3.5 Gráfico com os vetores
library(factoextra)
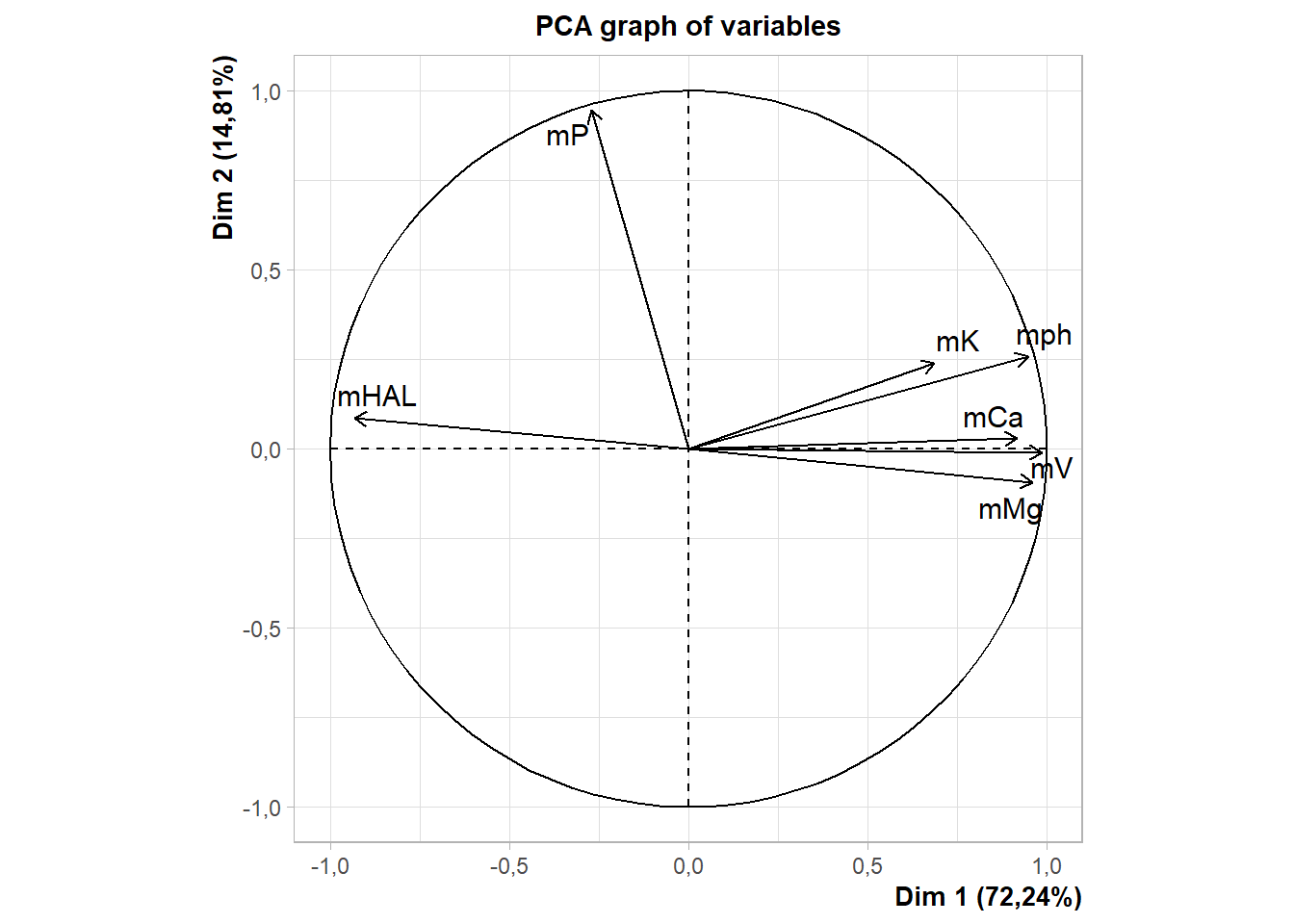
fviz_pca_var(pca)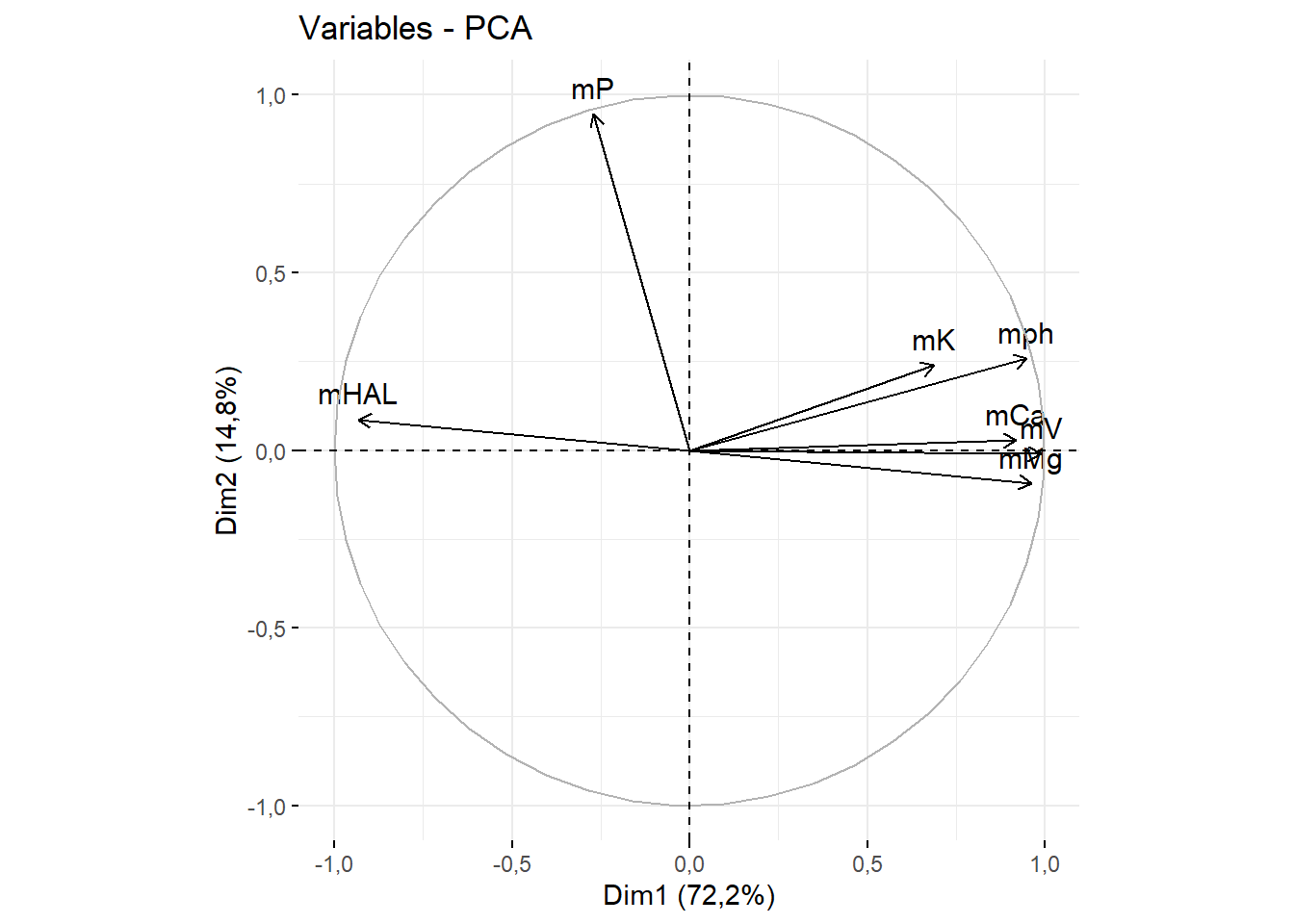
15.3.6 Renomeando eixos
fviz_pca_var(pca)+ylab("CP2 (14,9)")+xlab("CP1 (72,3%)")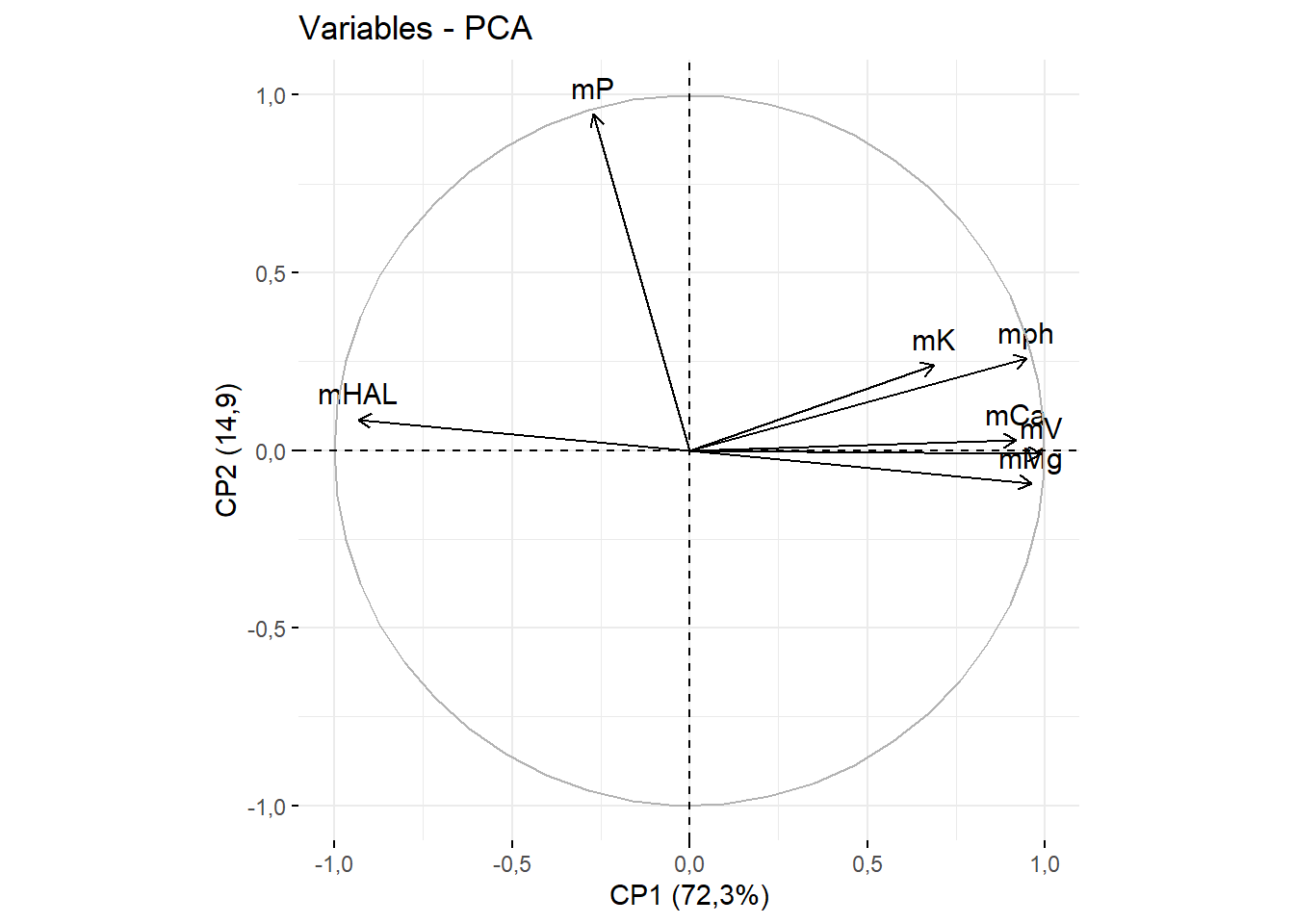
15.3.7 Removendo título
fviz_pca_var(pca, title="")+ylab("CP2 (14,9)")+xlab("CP1 (72,3%)")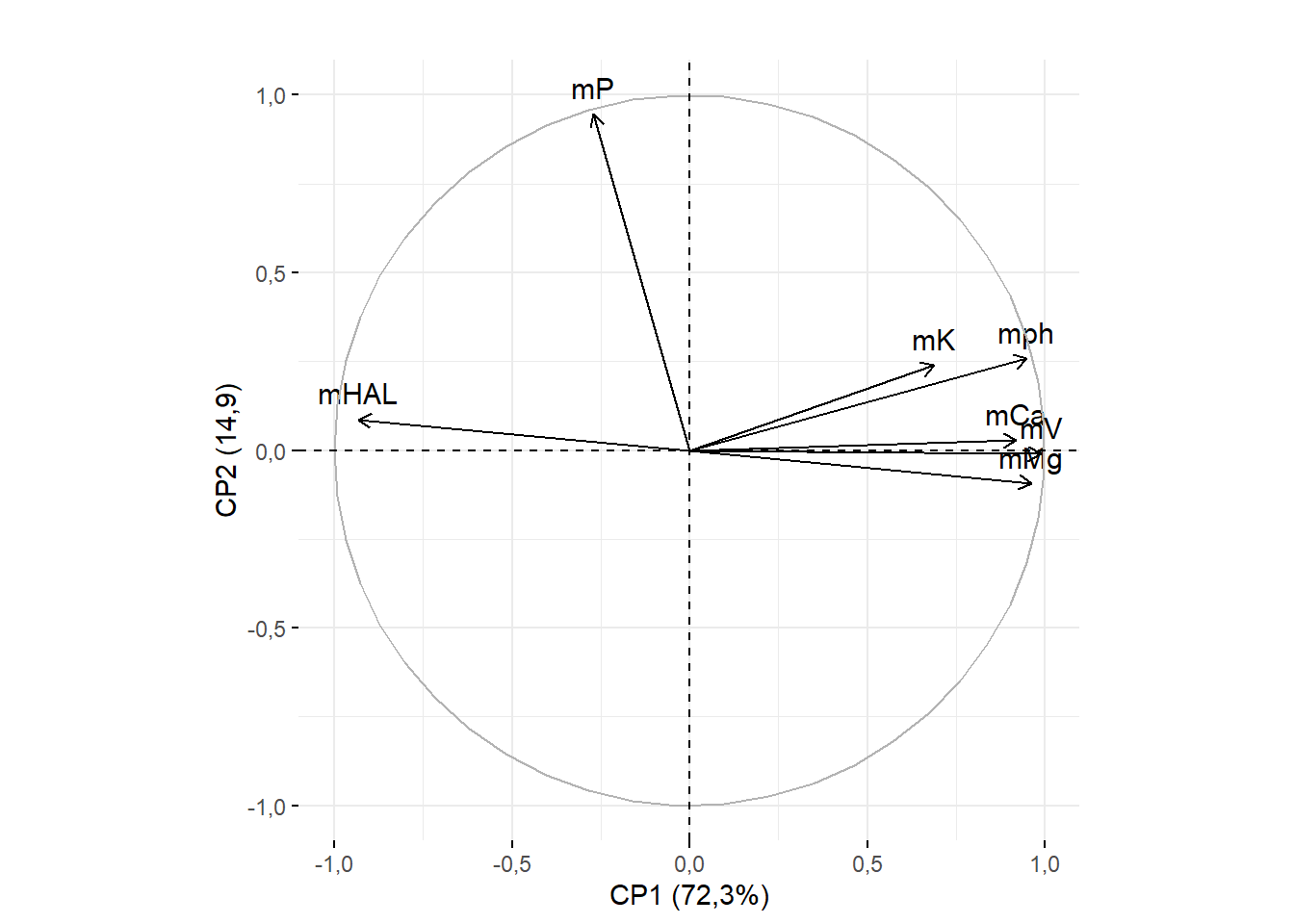
15.3.8 Renomeando os vetores
rownames(pca$var$coord)=c("pH","H+AL","K","P","Ca","Mg","V")
fviz_pca_var(pca, title="")+ylab("CP2 (14,9)")+xlab("CP1 (72,3%)")
15.3.9 Sobreposição dos nomes
rownames(pca$var$coord)=c("pH","H+AL","K","P","Ca","Mg","V")
fviz_pca_var(pca,
title="",
repel=T)+ylab("CP2 (14,9)")+xlab("CP1 (72,3%)")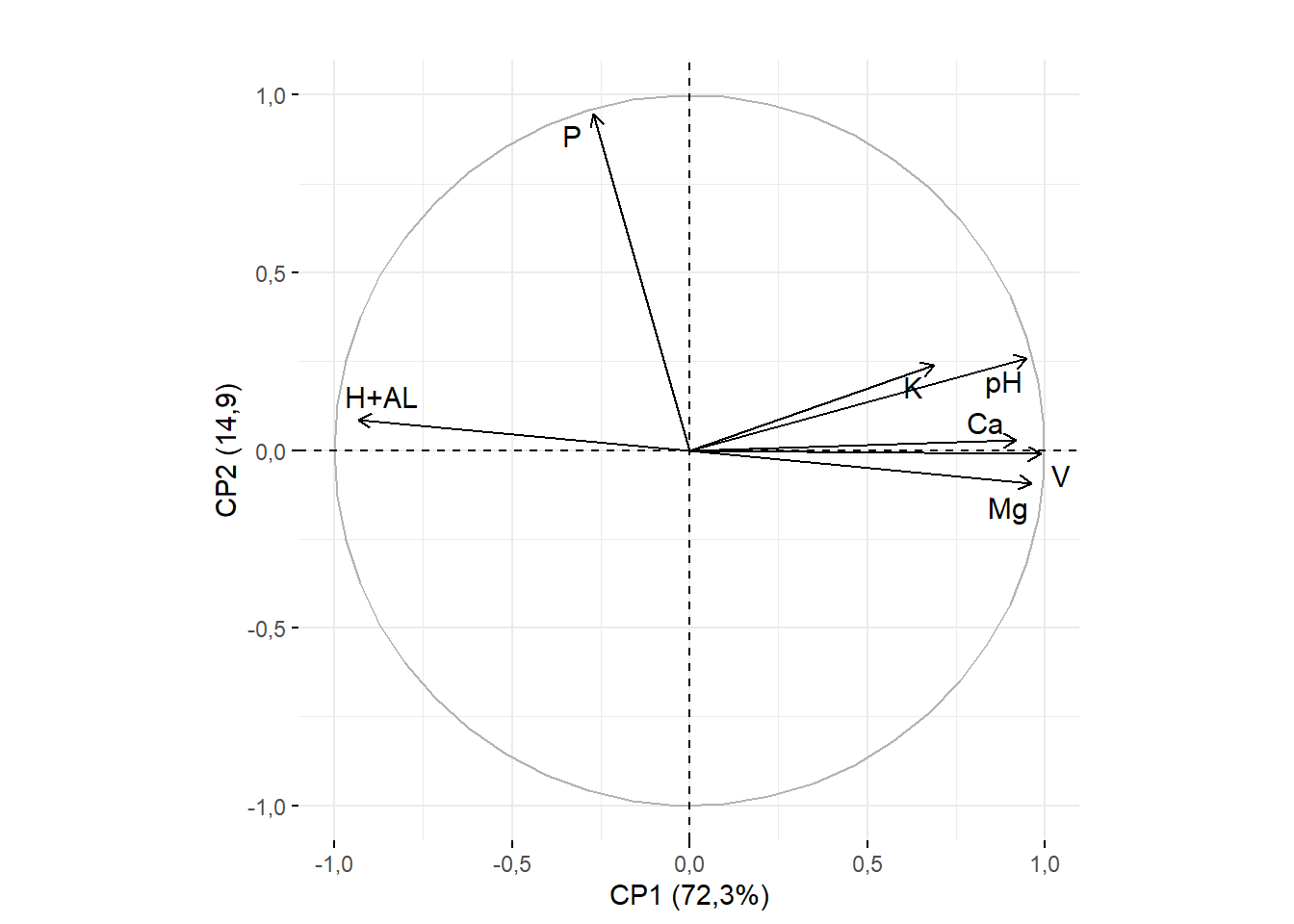
15.3.10 Removendo linhas de grade
rownames(pca$var$coord)=c("pH","H+AL","K","P","Ca","Mg","V")
fviz_pca_var(pca,
title="",
repel=T)+
ylab("CP2 (14,9)")+
xlab("CP1 (72,3%)")+
theme_classic()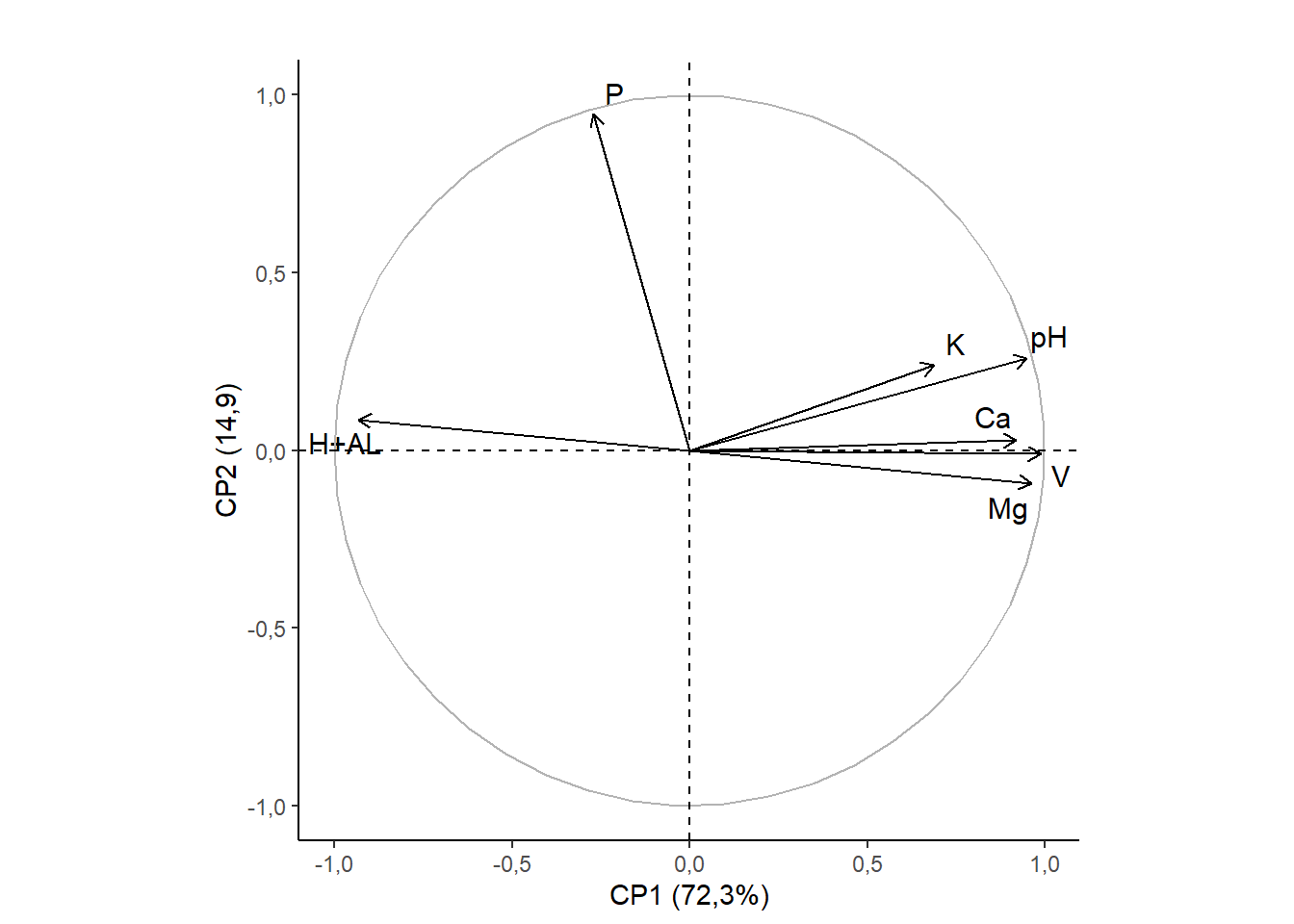
15.3.11 Pontos dos scores
fviz_pca_ind(pca)
15.3.12 Renomeando eixos e título
fviz_pca_ind(pca, title="")+ylab("CP2 (14,9)")+xlab("CP1 (72,3%)")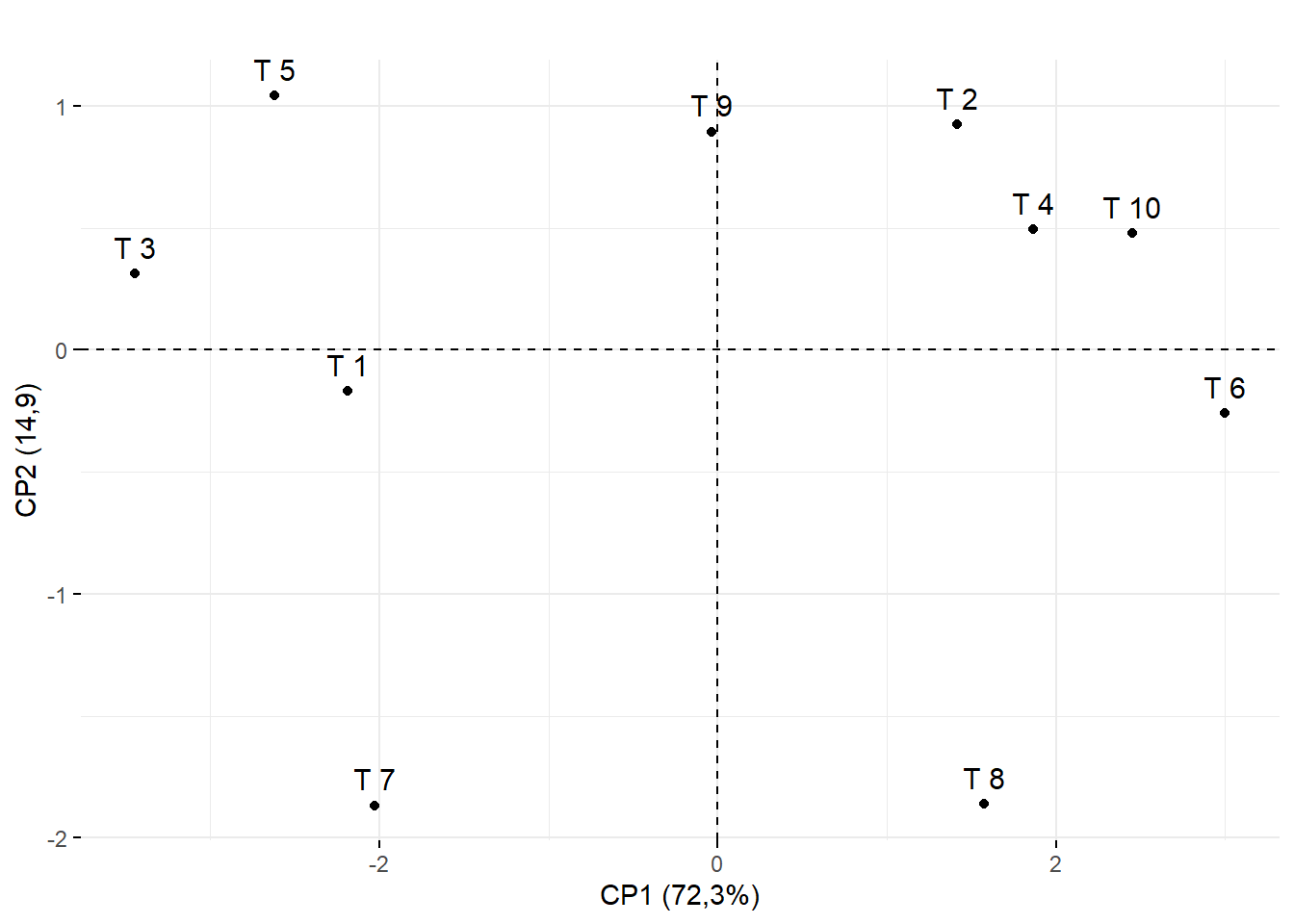
15.3.13 Marcando os clusters (Por coloração)
## Cluster 1: T8, T10, T6,T9,T2,T4
## Cluster 2: T7, T3, T1, T5
## Construir vetor com o cluster (Nesse caso vamos chamar de A e B)
cluster=c("B","A","B","A","B","A","B","A","A","A")
fviz_pca_ind(pca,
title="",
col.ind = as.factor(cluster))+
ylab("CP2 (14,9)")+
xlab("CP1 (72,3%)")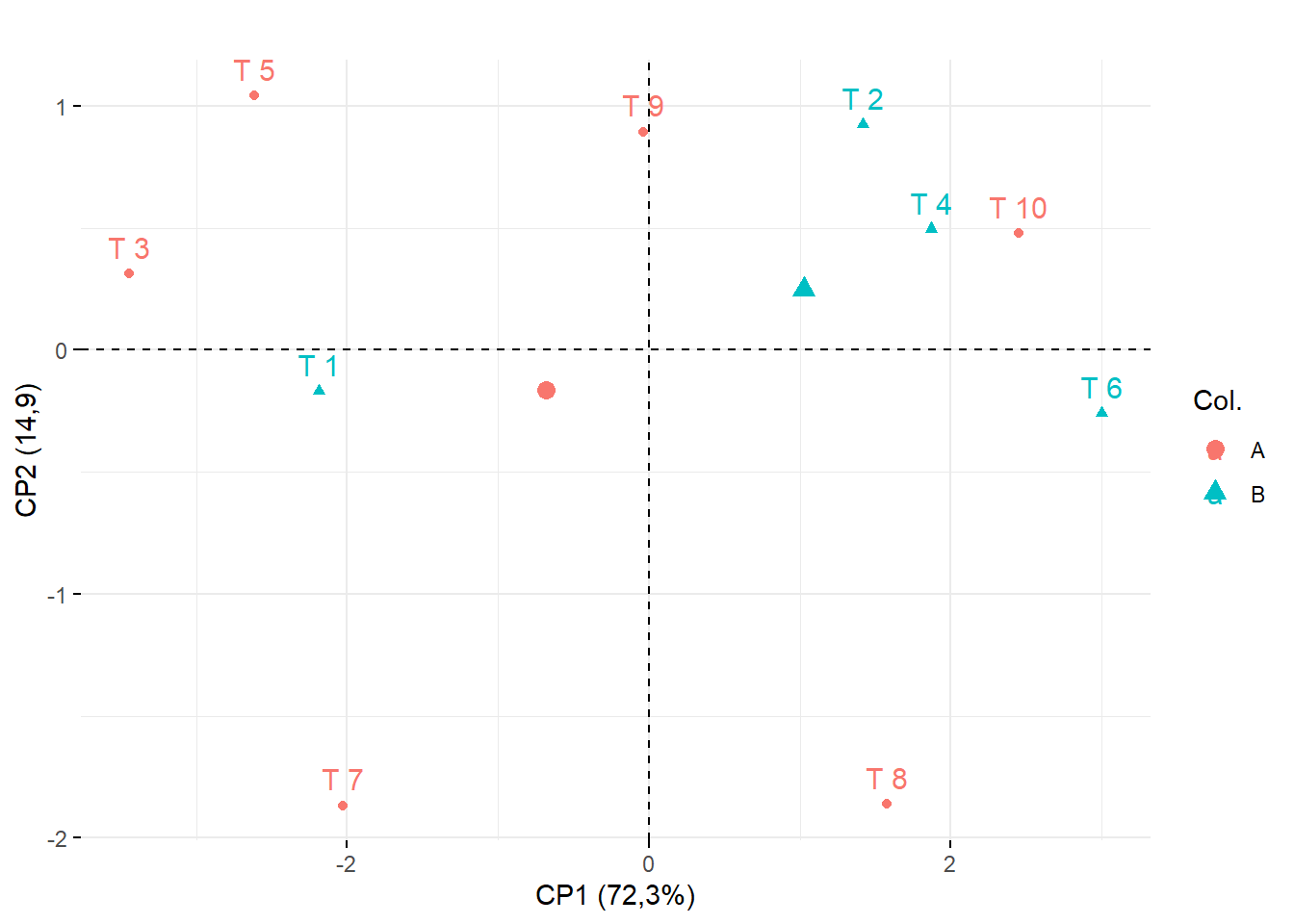
15.3.14 Marcando os clusters (Por formato de ponto)
## Cluster 1: T8, T10, T6,T9,T2,T4
## Cluster 2: T7, T3, T1, T5
## Construir vetor com o cluster (Nesse caso vamos chamar de A e B)
cluster=c("B","A","B","A","B","A","B","A","A","A")
fviz_pca_ind(pca,
title="",
pointshape = as.factor(cluster),
pointsize=2)+
ylab("CP2 (14,9)")+
xlab("CP1 (72,3%)")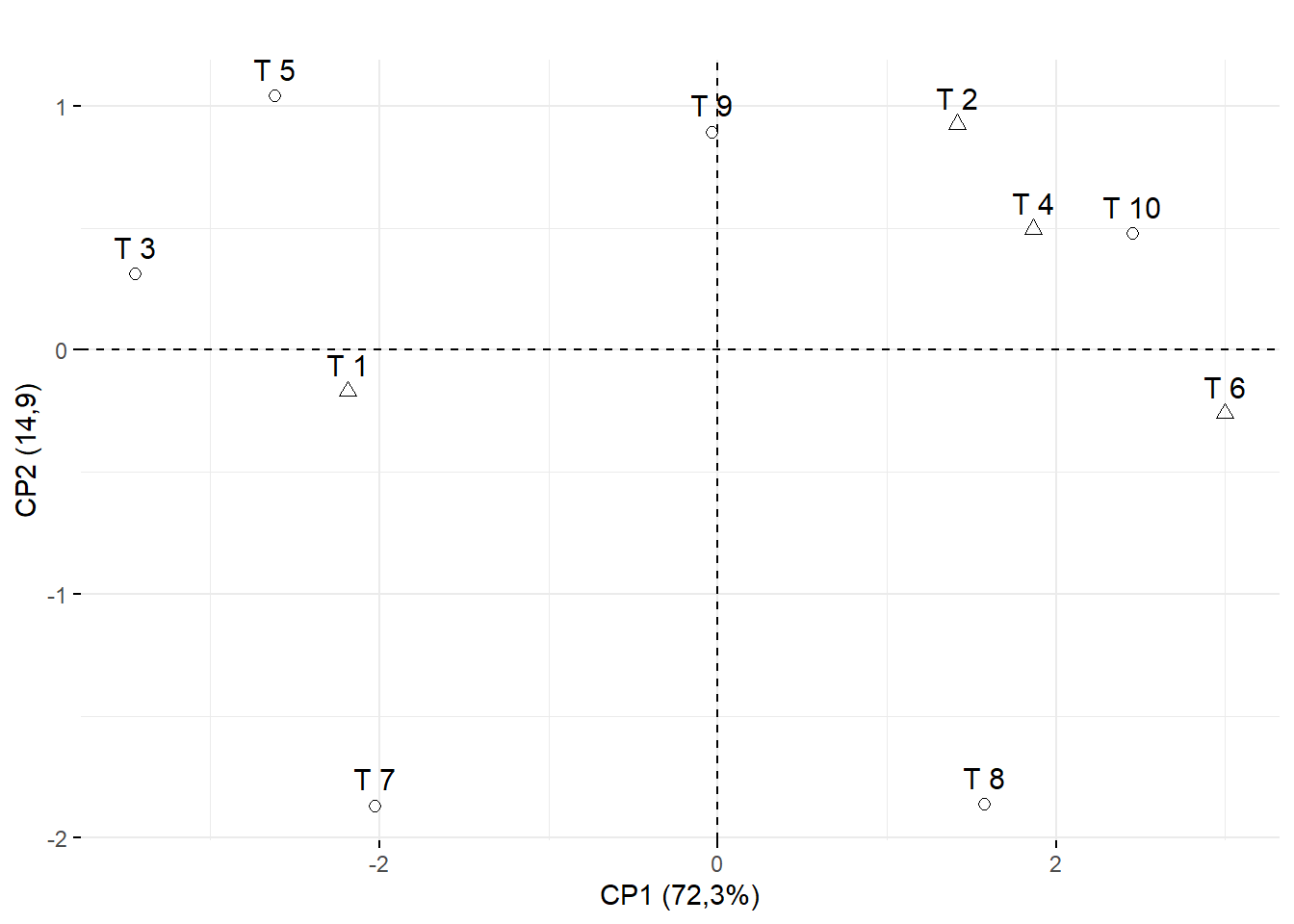
15.3.15 Marcando os clusters (Por coloração e formato de ponto)
## Cluster 1: T8, T10, T6,T9,T2,T4
## Cluster 2: T7, T3, T1, T5
## Construir vetor com o cluster (Nesse caso vamos chamar de A e B)
cluster=c("B","A","B","A","B","A","B","A","A","A")
fviz_pca_ind(pca,
title="", legend.title="Cluster",
habillage = as.factor(cluster))+
ylab("CP2 (14,9)")+
xlab("CP1 (72,3%)")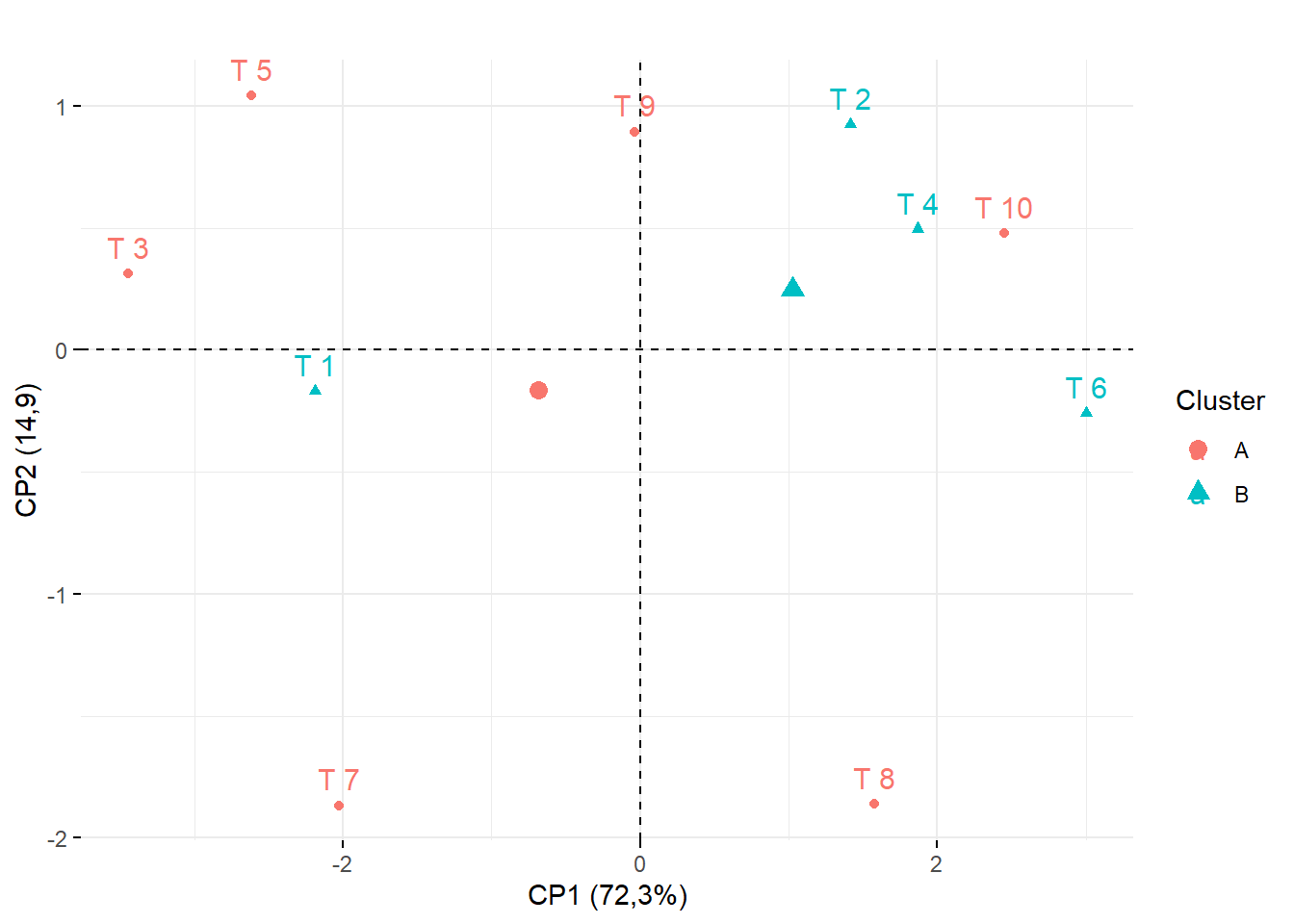
15.3.16 Removendo linhas de grade
## Cluster 1: T8, T10, T6,T9,T2,T4
## Cluster 2: T7, T3, T1, T5
## Construir vetor com o cluster (Nesse caso vamos chamar de A e B)
cluster=c("B","A","B","A","B","A","B","A","A","A")
fviz_pca_ind(pca,
title="", legend.title="Cluster",
habillage = as.factor(cluster))+
ylab("CP2 (14,9)")+
xlab("CP1 (72,3%)")+theme_classic()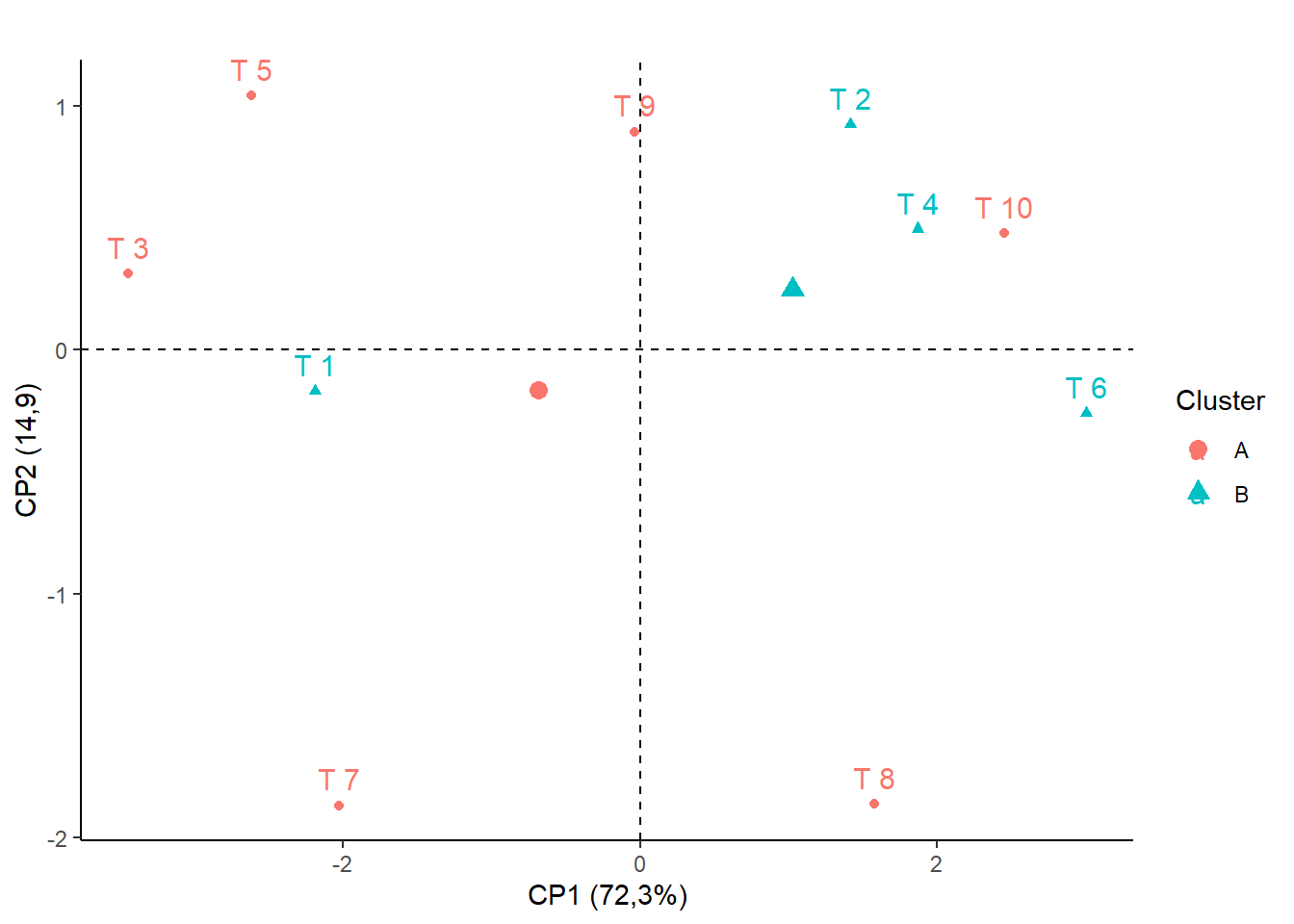
a=fviz_pca_ind(pca, title="")+theme_classic()
b=fviz_pca_var(pca, title="")+theme_classic()
library(gridExtra)
grid.arrange(a,b, ncol=2)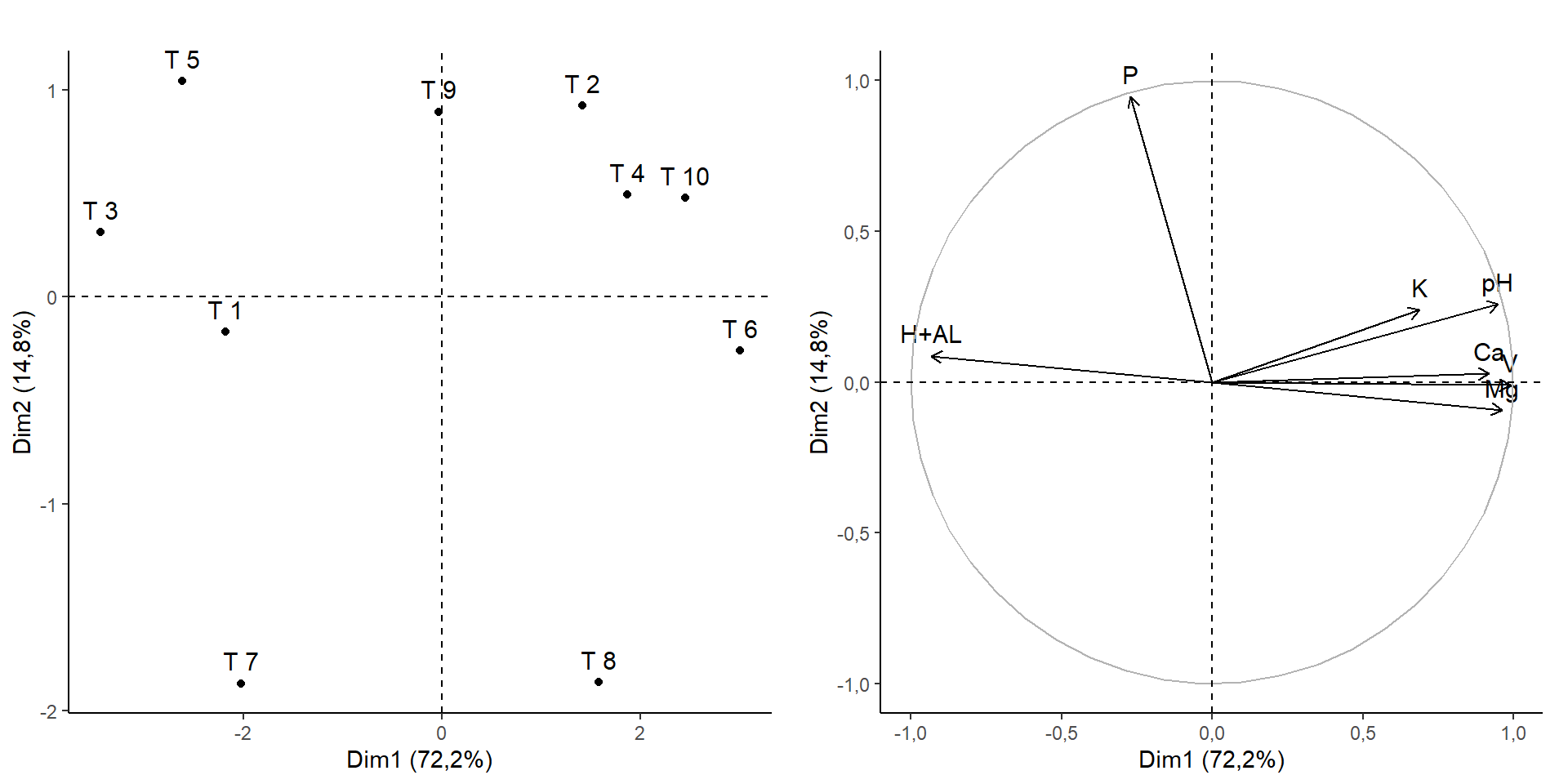
15.4 Gráfico de CP (Manualmente)
15.4.1 Calculando as médias
mph=tapply(ph, Trat, mean)
mHAL=tapply(HAL, Trat, mean)
mK=tapply(K, Trat, mean)
mP=tapply(P, Trat, mean)
mCa=tapply(Ca, Trat, mean)
mMg=tapply(Mg, Trat, mean)
mV=tapply(V, Trat, mean)
dadosm=data.frame(mph,mHAL,mK,mP,mCa,mMg,mV)15.4.2 Dendrograma (Definir Clusters)
Obs. Fica a critério do pesquisador o valor do corte (Neste caso optei pelo corte em 8, formando assim dois clusters)
Podemos fazer como neste exemplo abaixo:
dend=as.dendrogram(hclust(dist(dadosm), method='average'), hang = -1)
plot(dend)
abline(h=8, lty=2, col="red")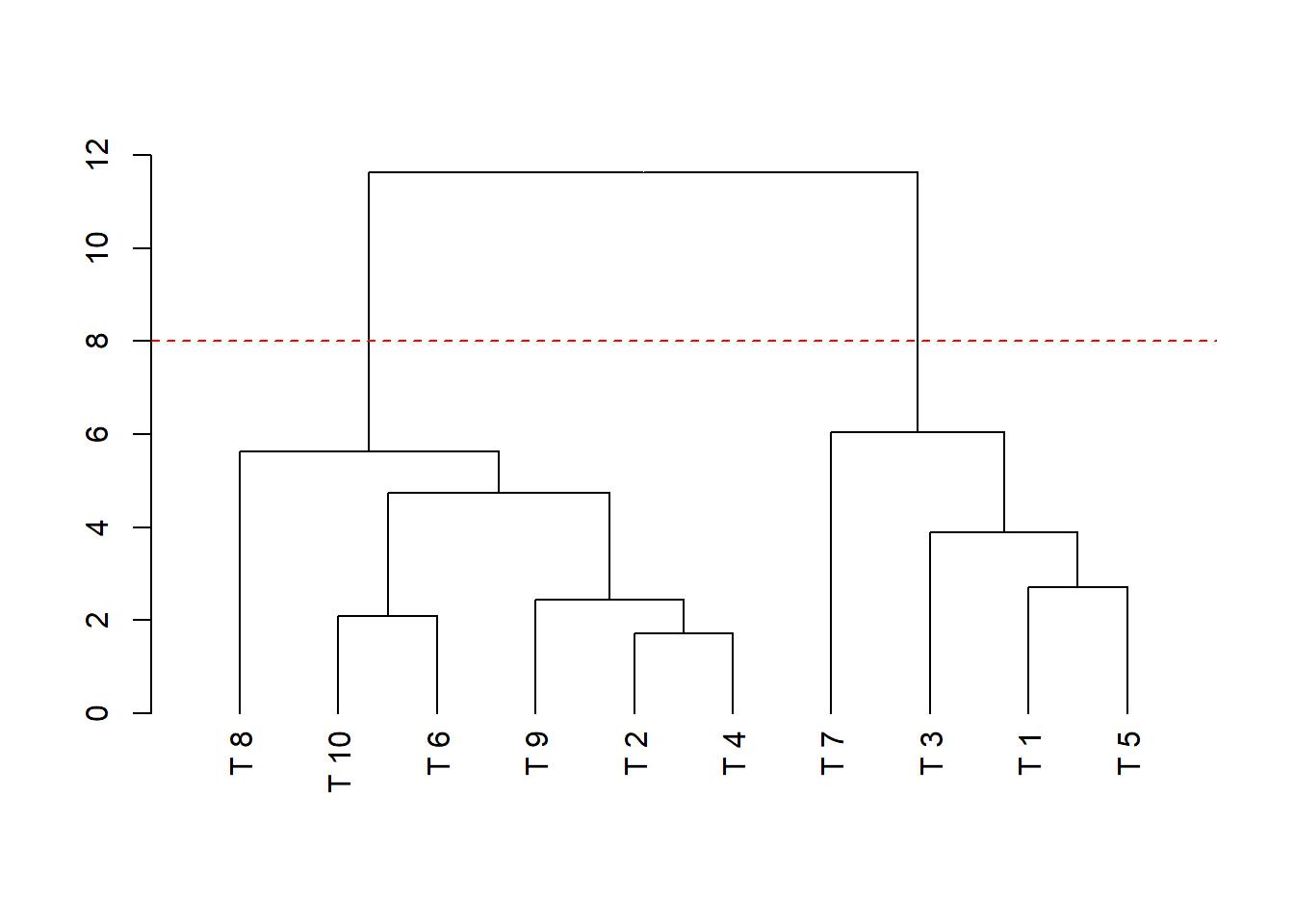
## Cluster 1: T8, T10, T6,T9,T2,T4
## Cluster 2: T7, T3, T1, T5ou,
library(dendextend)
dend=as.dendrogram(hclust(dist(dadosm), method='average'))
dend=set(dend,"branches_k_color", value = c("red", "blue"), k = 2)
par(cex=0.7, mai=c(1.2,0.8,0.5,0.5))
plot(dend,las=1,ylab="Distância")
par(cex=0.8)
rect.dendrogram(dend, k=2,border = 8, lty = 5, lwd = 2)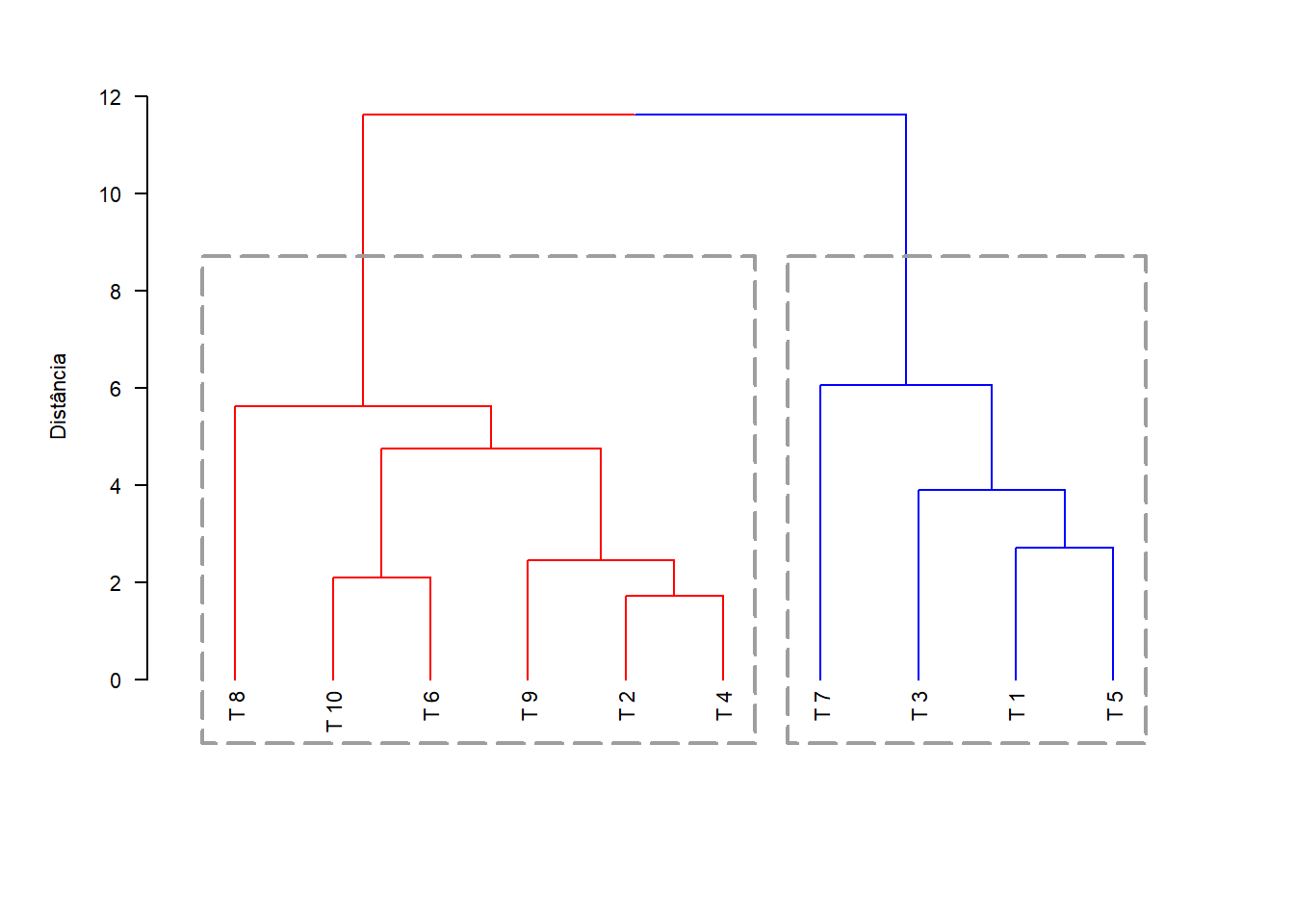
15.4.3 Valores dos CP
require(FactoMineR)
pca=PCA(dadosm,scale.unit=T,graph=F)
round(pca$eig,3)## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 5,057 72,243 72,243
## comp 2 1,037 14,812 87,055
## comp 3 0,639 9,128 96,183
## comp 4 0,237 3,387 99,571
## comp 5 0,022 0,312 99,883
## comp 6 0,008 0,109 99,992
## comp 7 0,001 0,008 100,00015.4.4 Gráfico com os componentes
plot(pca$eig[,2], type="b",ylab="Porcentagem de variância",xlab="CP")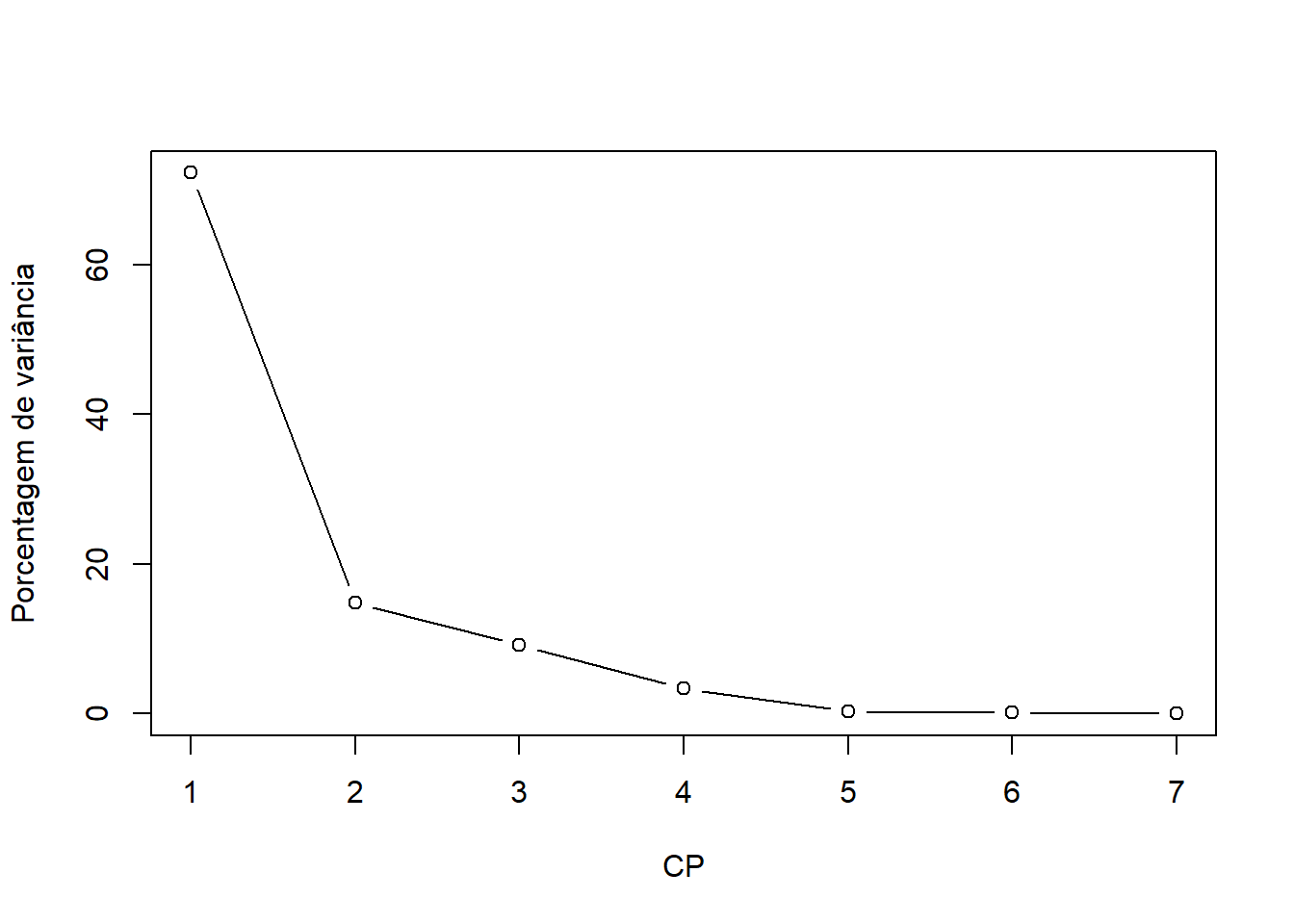
15.4.5 Ponto dos scores
plot(pca$ind$coord, # Extraindo da pca os valores das coordenadas em x e CP1 e y e CP2
xlab="CP1 (72.2 %)", # renomeando eixo x
ylab="CP2 (14.8 %)", # renomeando eixo y
pch=16) # alterando formato de ponto ("Bolinha preenchida")
abline(h=0,v=0, lty=2) # traçando linha em x e y = 0; lty=2 é linha tracejada 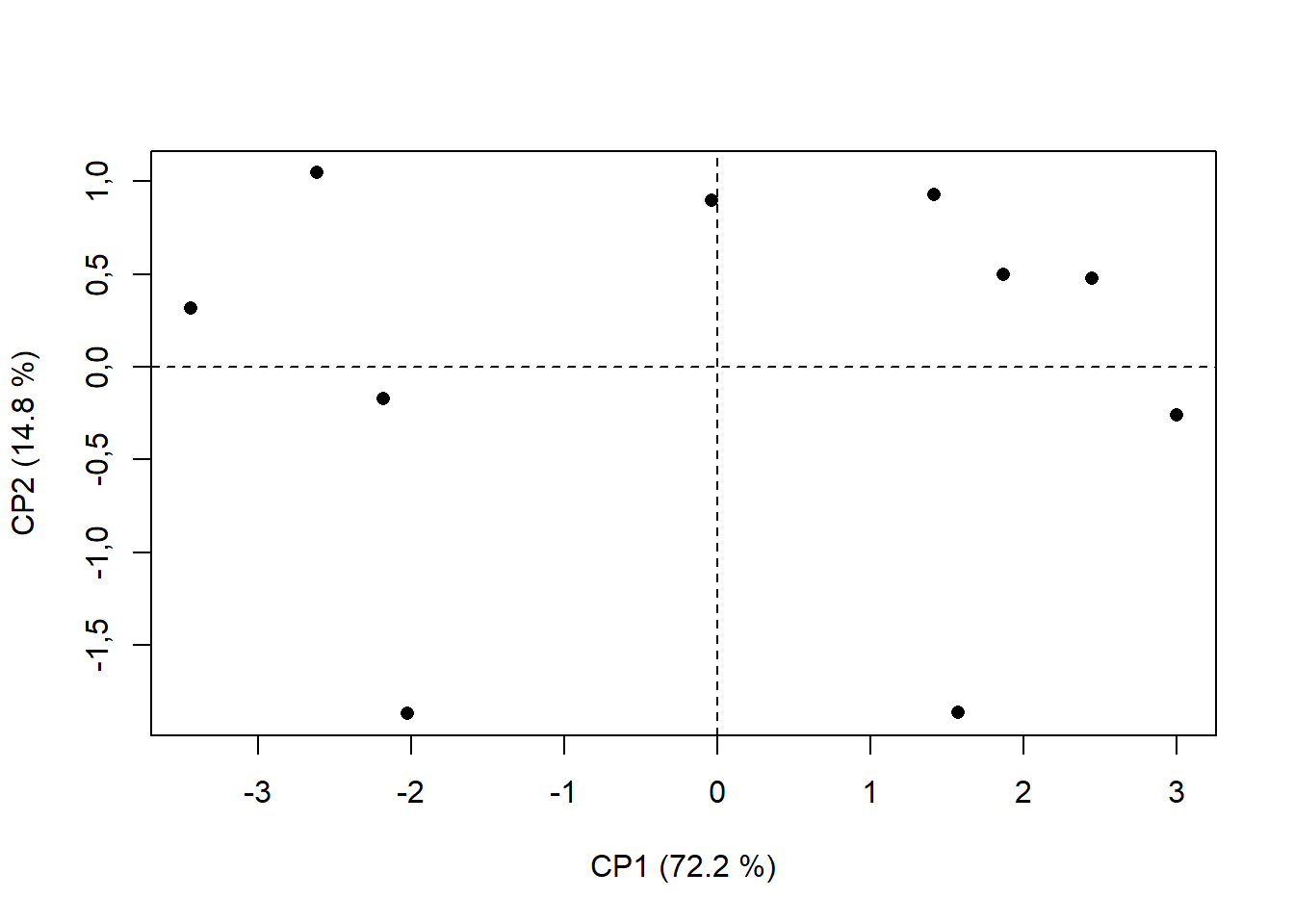
15.4.6 Identificando pontos
plot(pca$ind$coord, # Extraindo da pca os valores das coordenadas em x e CP1 e y e CP2
xlab="CP1 (72.2 %)", # renomeando eixo x
ylab="CP2 (14.8 %)", # renomeando eixo y
pch=16) # alterando formato de ponto ("Bolinha preenchida")
abline(h=0,v=0, lty=2) # traçando linha em x e y = 0; lty=2 é linha tracejada
text(pca$ind$coord[,1],
pca$ind$coord[,2]-0.1,
rownames(pca$ind$coord))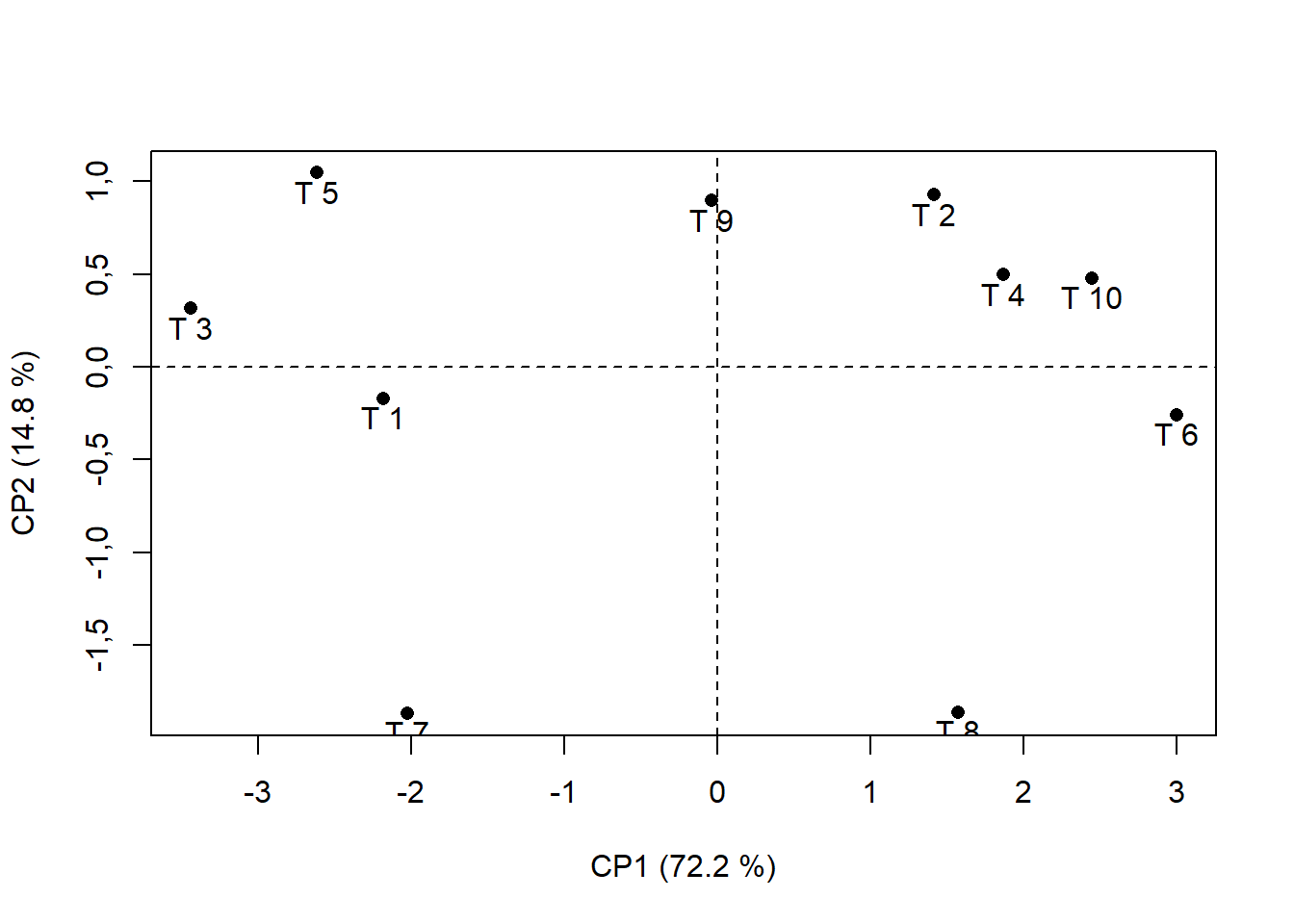
15.4.7 Modificando nome dos pontos
rownames(pca$ind$coord)=c("A","J","B","C","D","E","F","G","H","I")
plot(pca$ind$coord, # Extraindo da pca os valores das coordenadas em x e CP1 e y e CP2
xlab="CP1 (72.2 %)", # renomeando eixo x
ylab="CP2 (14.8 %)", # renomeando eixo y
pch=16) # alterando formato de ponto ("Bolinha preenchida")
abline(h=0,v=0, lty=2) # traçando linha em x e y = 0; lty=2 é linha tracejada
text(pca$ind$coord[,1],
pca$ind$coord[,2]-0.1,
rownames(pca$ind$coord))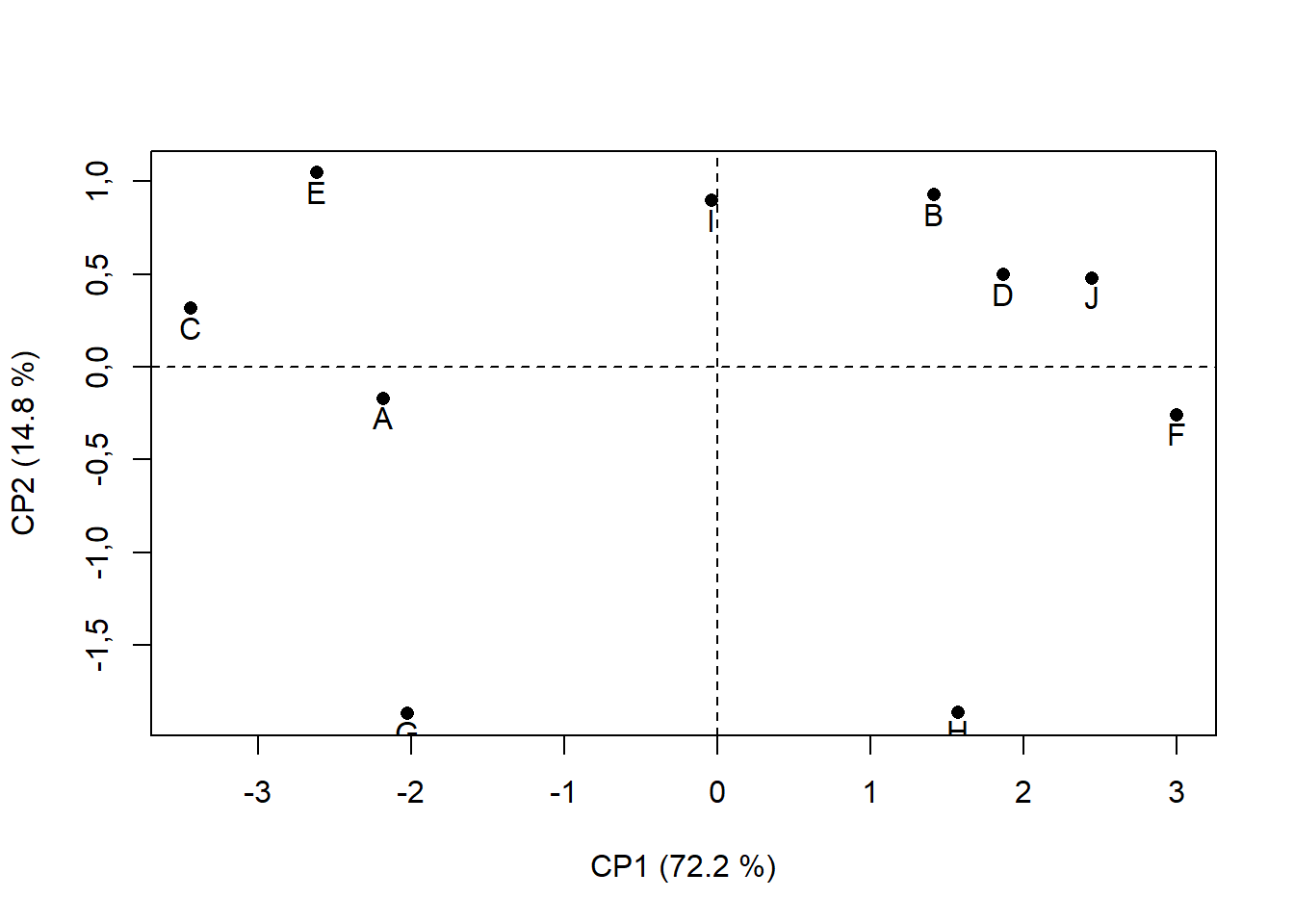
15.4.8 Limite da seta dos vetores
plot(pca$var$coord, # Extraindo da pca os valores da coordenadas em x e y dos vetores resposta
xlab="CP1 (72.2 %)", # renomeando eixo x
ylab="CP2 (14.8 %)", # renomeando eixo y
pch=16, # alterando formato de ponto ("Bolinha preenchida")
ylim=c(-1,1), # Alterando escala de Y para -1 até 1
xlim=c(-1,1)) # Alterando escala de X para -1 até 1
abline(h=0,v=0, lty=2) # traçando linha em x e y = 0; lty=2 é linha tracejada 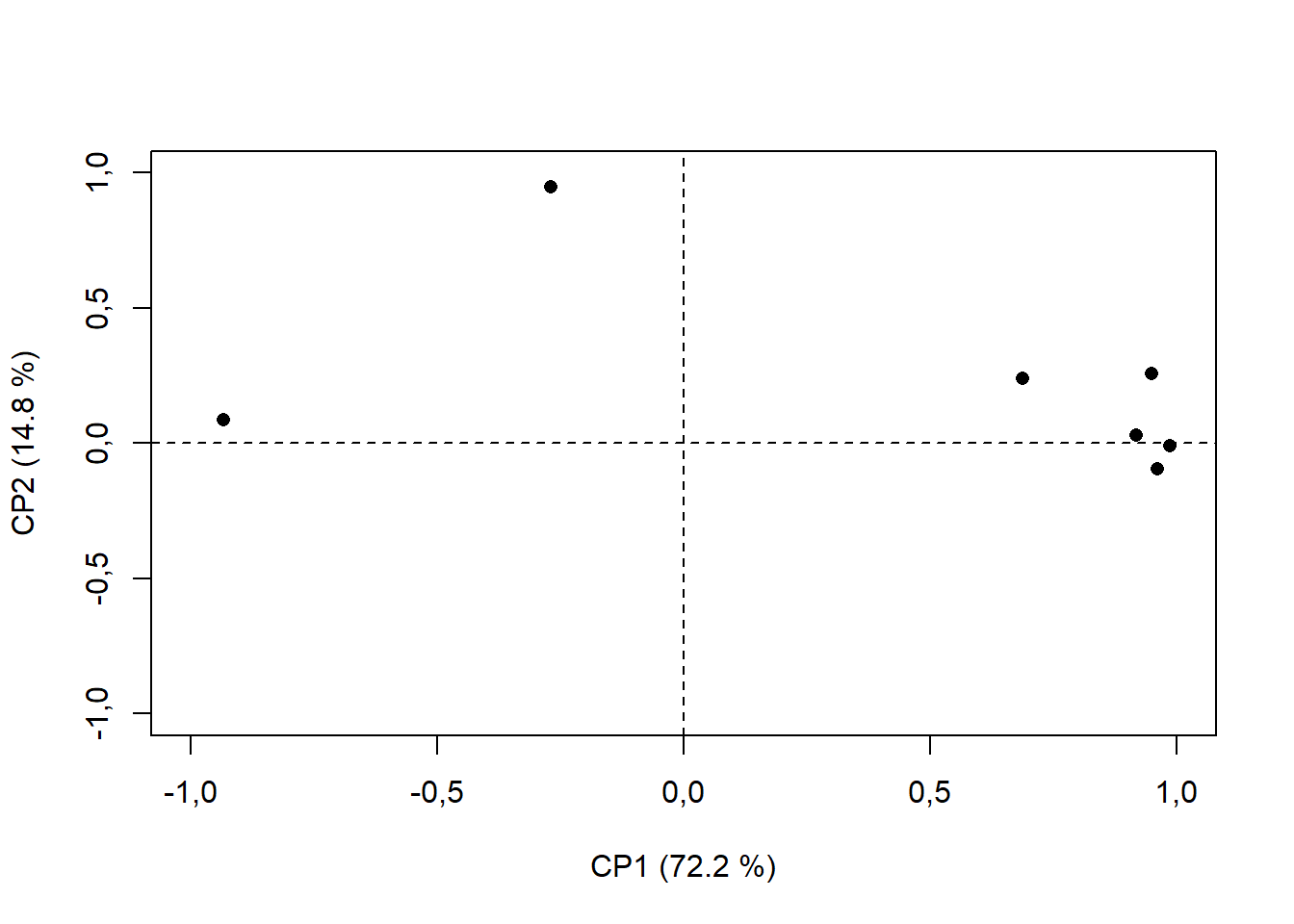
15.4.9 Convertendo o ponto para seta
Neste caso, temos que criar setas individuais e plotar sobre o nosso gráfico.
Ex.
pca$var$coord[1,1]: extraindo depcao valor da coordenada X para o vetor 1, em que depca, localiza-se na linha 1 e coluna 1pca$var$coord[1,2]: extraindo depcao valor da coordenada y para o vetor 1, em que depca, localiza-se na linha 1 e coluna 2
plot(pca$var$coord,
xlab="CP1 (72.2 %)",
ylab="CP2 (14.8 %)",
col="white", # Estou definindo como branco para apagar os pontos
ylim=c(-1.5,1.5),
xlim=c(-1.5,1.5))
abline(h=0,v=0, lty=2)
arrows(0,0,pca$var$coord[1,1],pca$var$coord[1,2], length = 0.1) # vetor 1 - pH
arrows(0,0,pca$var$coord[2,1],pca$var$coord[2,2], length = 0.1) # vetor 2 - HAL
arrows(0,0,pca$var$coord[3,1],pca$var$coord[3,2], length = 0.1) # vetor 3 - K
arrows(0,0,pca$var$coord[4,1],pca$var$coord[4,2], length = 0.1) # vetor 4 - P
arrows(0,0,pca$var$coord[5,1],pca$var$coord[5,2], length = 0.1) # vetor 5 - Ca
arrows(0,0,pca$var$coord[6,1],pca$var$coord[6,2], length = 0.1) # vetor 6 - Mg
arrows(0,0,pca$var$coord[7,1],pca$var$coord[7,2], length = 0.1) # vetor 7 - V
text(pca$var$coord-0.01,rownames(pca$var$coord)) # Estou colocando os nomes dos vetores (-0.01 significa abaixo da coordenada a 0.01)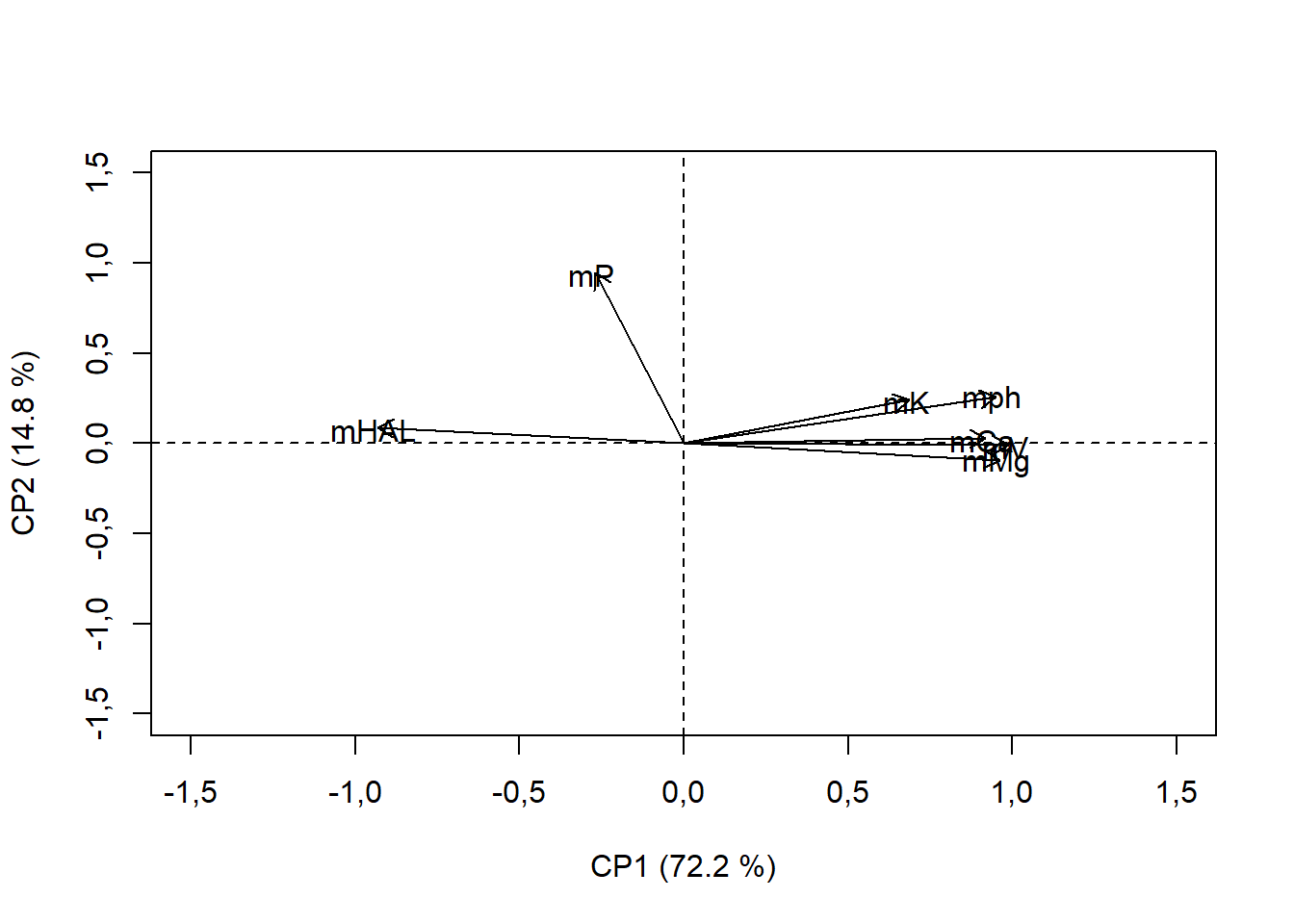
15.4.10 Alterando posição do nome do vetores
Existem pesquisadores que preferem que o nome dos vetores quando x é positivo esteja a direita da extremidade da seta e quando x é negativo, o nome esteja a esquerda da seta. Neste caso, podemos utilizar a função ifelse dentro de text()
plot(pca$var$coord,
xlab="CP1 (72.2 %)",
ylab="CP2 (14.8 %)",
col="white",
ylim=c(-0.5,1),
xlim=c(-1.5,1.5))
abline(h=0,v=0, lty=2)
arrows(0,0,pca$var$coord[1,1],pca$var$coord[1,2], length = 0.1)
arrows(0,0,pca$var$coord[2,1],pca$var$coord[2,2], length = 0.1)
arrows(0,0,pca$var$coord[3,1],pca$var$coord[3,2], length = 0.1)
arrows(0,0,pca$var$coord[4,1],pca$var$coord[4,2], length = 0.1)
arrows(0,0,pca$var$coord[5,1],pca$var$coord[5,2], length = 0.1)
arrows(0,0,pca$var$coord[6,1],pca$var$coord[6,2], length = 0.1)
arrows(0,0,pca$var$coord[7,1],pca$var$coord[7,2], length = 0.1)
text(pca$var$coord[,1]+
ifelse(pca$var$coord[,1]<0,-0.2,+0.2),
pca$var$coord[,2],rownames(pca$var$coord))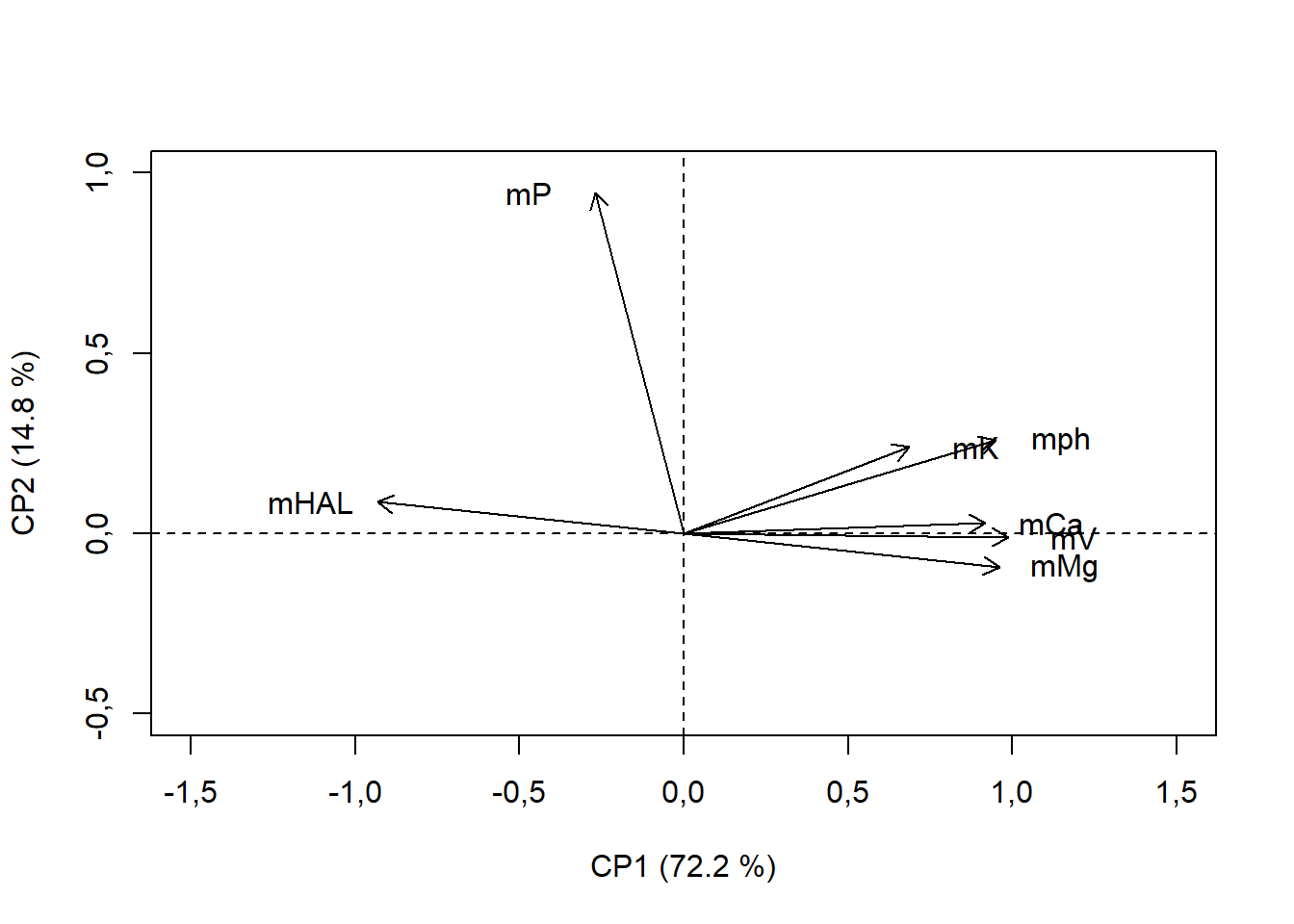
ifelse(pca$var$coord[,1]<0,-0.2,+0.2): estamos definindo que se pca$var$coord[,1] for menor que 0, irá adicionar -0.2, do contrário irá somar 0.2
Obs. Nessa caso estamos alterando apenas em X, este princípio também pode ser aplicado em Y. Também é possível estabelecer manualmente a localização do texto (Criar um vetor com as coordenadas)
15.4.11 Adicionando círculo com raio do maior vetor resposta
library(plotrix)
plot(pca$var$coord,
xlab="CP1 (72.2 %)",
ylab="CP2 (14.8 %)",
col="white",
ylim=c(-1,1),
xlim=c(-1.5,1.5))
abline(h=0,v=0, lty=2)
arrows(0,0,pca$var$coord[1,1],pca$var$coord[1,2], length = 0.1)
arrows(0,0,pca$var$coord[2,1],pca$var$coord[2,2], length = 0.1)
arrows(0,0,pca$var$coord[3,1],pca$var$coord[3,2], length = 0.1)
arrows(0,0,pca$var$coord[4,1],pca$var$coord[4,2], length = 0.1)
arrows(0,0,pca$var$coord[5,1],pca$var$coord[5,2], length = 0.1)
arrows(0,0,pca$var$coord[6,1],pca$var$coord[6,2], length = 0.1)
arrows(0,0,pca$var$coord[7,1],pca$var$coord[7,2], length = 0.1)
text(pca$var$coord[,1]+ifelse(pca$var$coord[,1]<0,-0.2,+0.2),
pca$var$coord[,2],rownames(pca$var$coord))
draw.circle(0,0,max(ifelse(c(pca$var$coord[,1],pca$var$coord[,2])<0,
c(pca$var$coord[,1],pca$var$coord[,2])*-1,
c(pca$var$coord[,1],pca$var$coord[,2]))))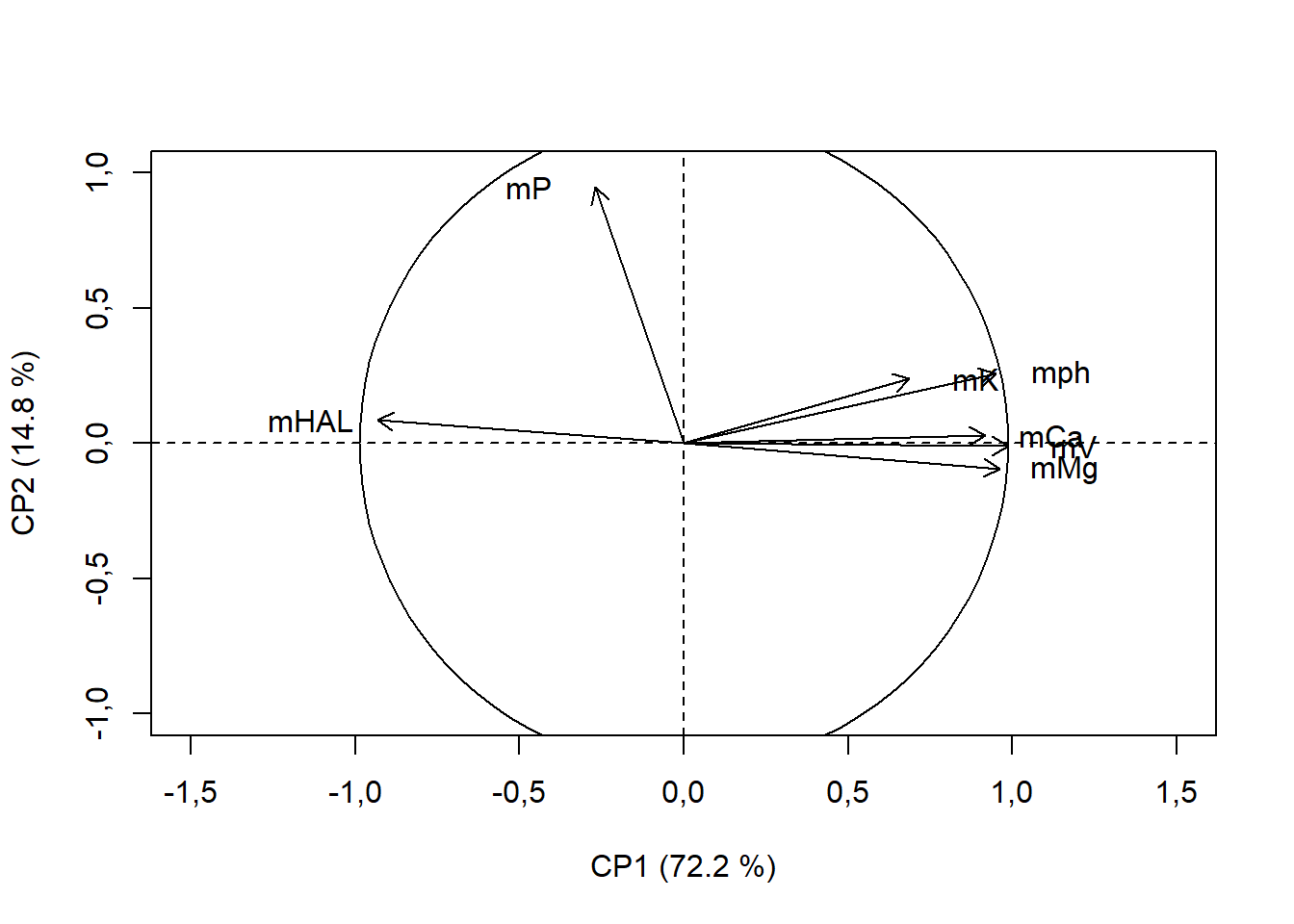
15.4.12 Renomeando vetores
rownames(pca$var$coord)=c("pH","H+AL","K","P","Ca","Mg","V%") # renomeando vetores
library(plotrix)
plot(pca$var$coord,
xlab="CP1 (72.2 %)",
ylab="CP2 (14.8 %)",
col="white",
ylim=c(-1,1),
xlim=c(-1.5,1.5))
abline(h=0,v=0, lty=2)
arrows(0,0,pca$var$coord[1,1],pca$var$coord[1,2], length = 0.1)
arrows(0,0,pca$var$coord[2,1],pca$var$coord[2,2], length = 0.1)
arrows(0,0,pca$var$coord[3,1],pca$var$coord[3,2], length = 0.1)
arrows(0,0,pca$var$coord[4,1],pca$var$coord[4,2], length = 0.1)
arrows(0,0,pca$var$coord[5,1],pca$var$coord[5,2], length = 0.1)
arrows(0,0,pca$var$coord[6,1],pca$var$coord[6,2], length = 0.1)
arrows(0,0,pca$var$coord[7,1],pca$var$coord[7,2], length = 0.1)
text(c(1.05, -1.1, 0.8, -0.3, 1, 1.05, 1.1),
c(0.3, 0.1, 0.3, 1, 0.06, -0.1, -0),
rownames(pca$var$coord))
draw.circle(0,0,max(ifelse(c(pca$var$coord[,1],pca$var$coord[,2])<0,
c(pca$var$coord[,1],pca$var$coord[,2])*-1,
c(pca$var$coord[,1],pca$var$coord[,2]))))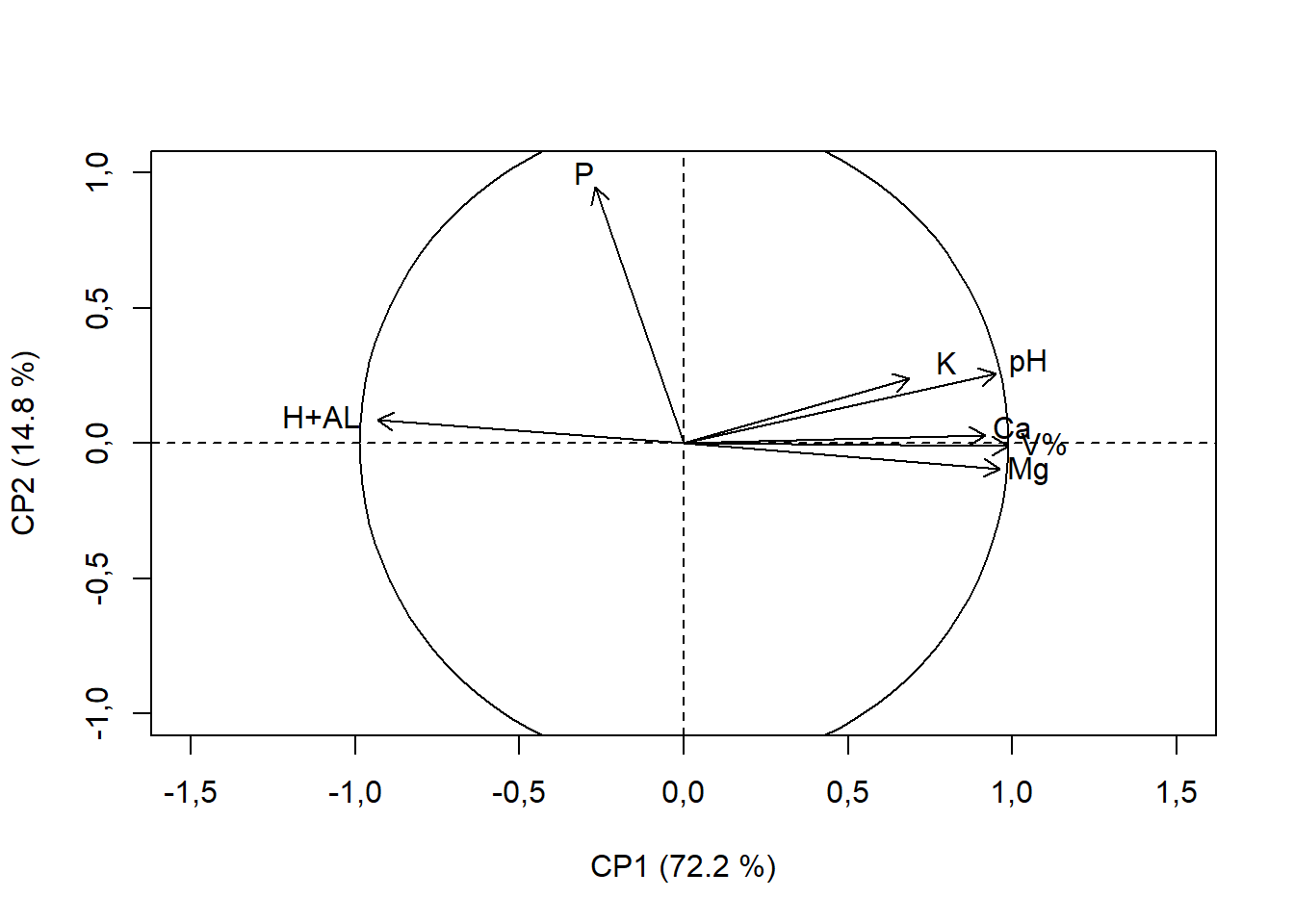
15.5 Screeplot
15.5.1 Conjunto de dados
Trat=rep(c(paste("T",1:10)), e=12)
dados=data.frame(Trat,ph,HAL,K,P,Ca,Mg,V)15.5.2 Calculando as médias
mph=tapply(ph, Trat, mean)
mHAL=tapply(HAL, Trat, mean)
mK=tapply(K, Trat, mean)
mP=tapply(P, Trat, mean)
mCa=tapply(Ca, Trat, mean)
mMg=tapply(Mg, Trat, mean)
mV=tapply(V, Trat, mean)
dadosm=data.frame(mph,mHAL,mK,mP,mCa,mMg,mV)15.5.3 Pacote FactomineR
library(FactoMineR)
pca=PCA(dadosm)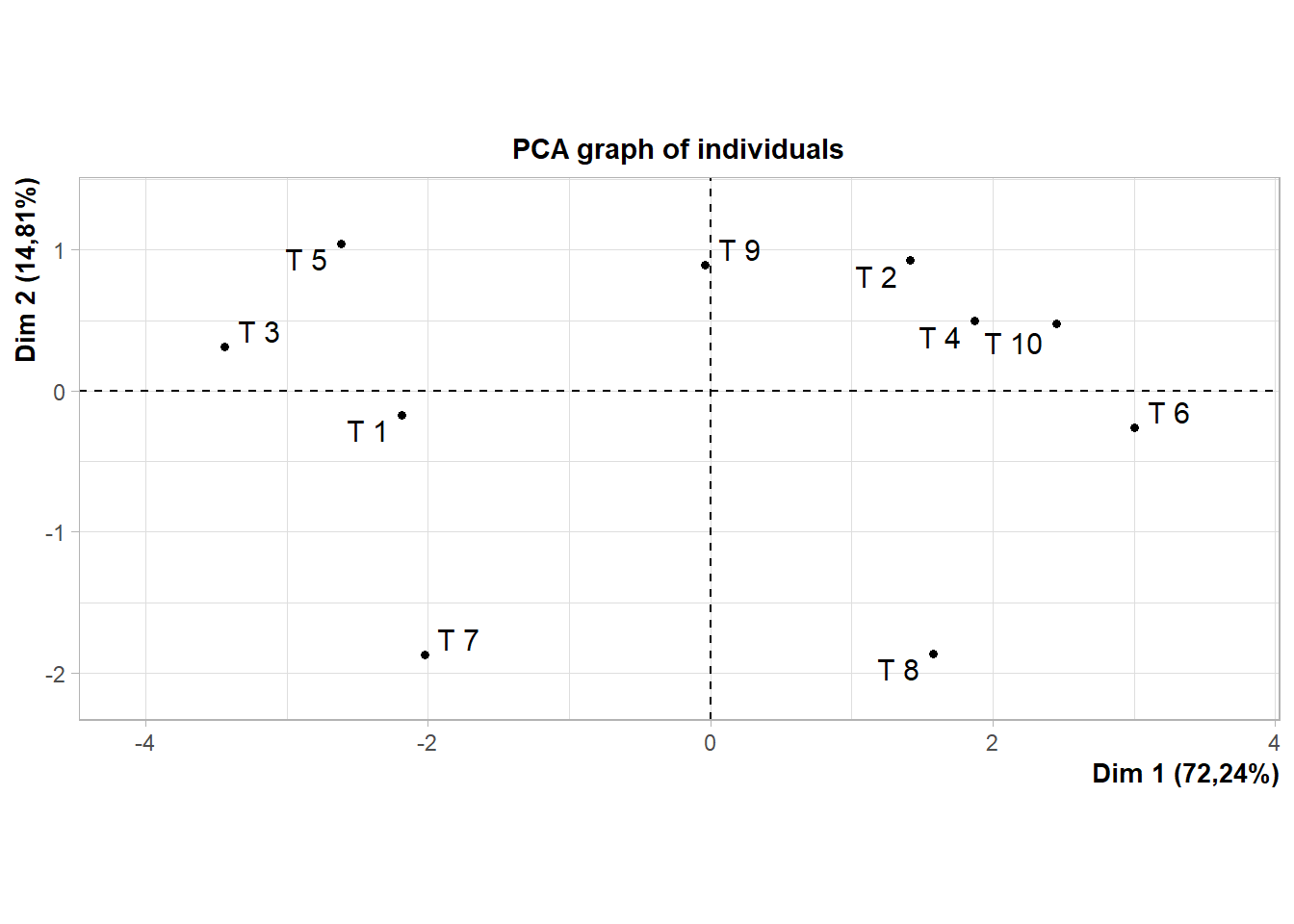
15.5.4 Screeplot do factoextra
library(factoextra)
fviz_screeplot(pca)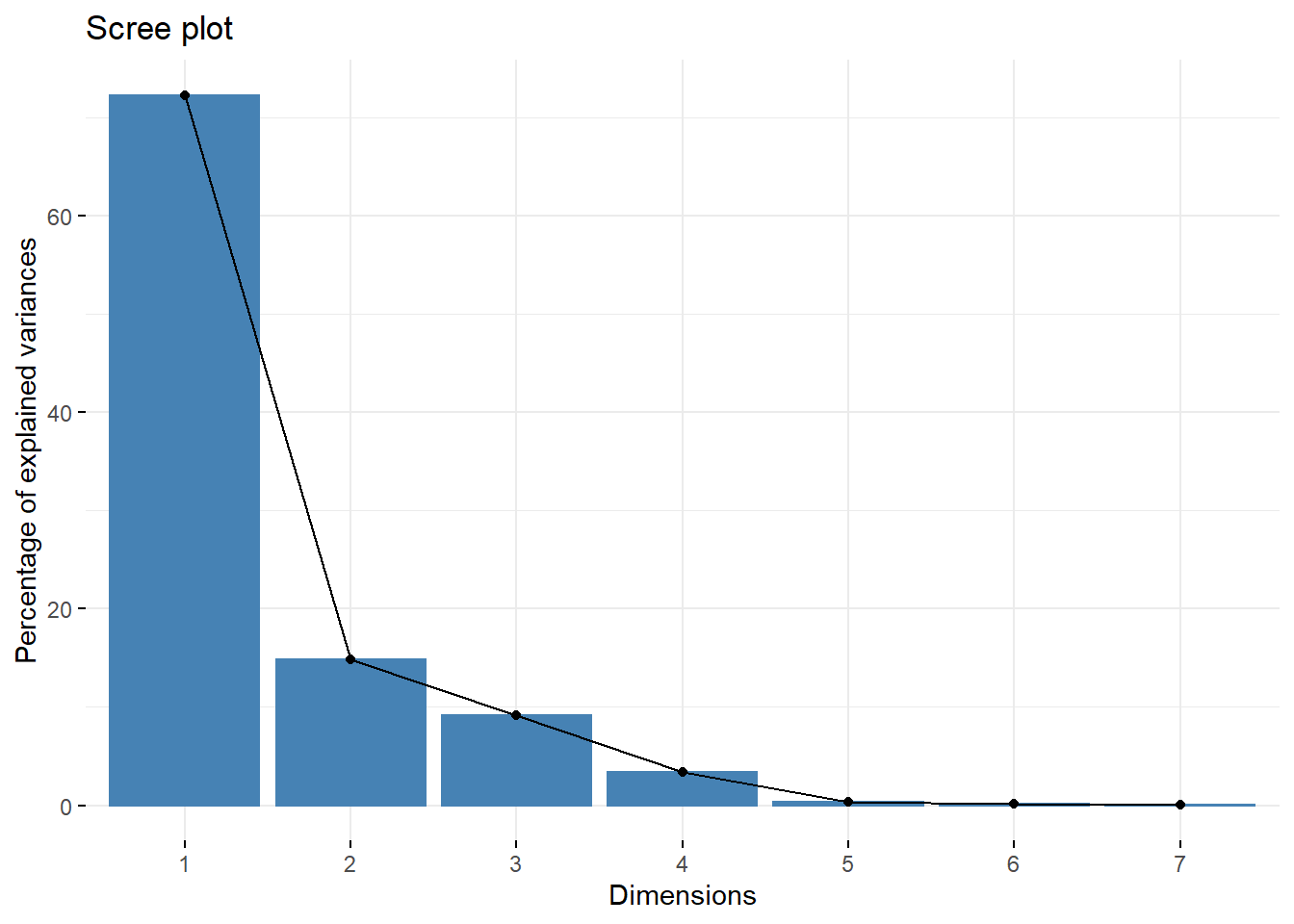
fviz_screeplot(pca,
title="", # removendo título
font.family="serif", # fonte times new roman
barcolor="black", # cor da borda preto
addlabels=T,
ggtheme=theme_classic())+
xlab("Componente Principal")+ # nomeando eixo x
ylab("Porcentagem de explicação da variância") # nomeando eixo y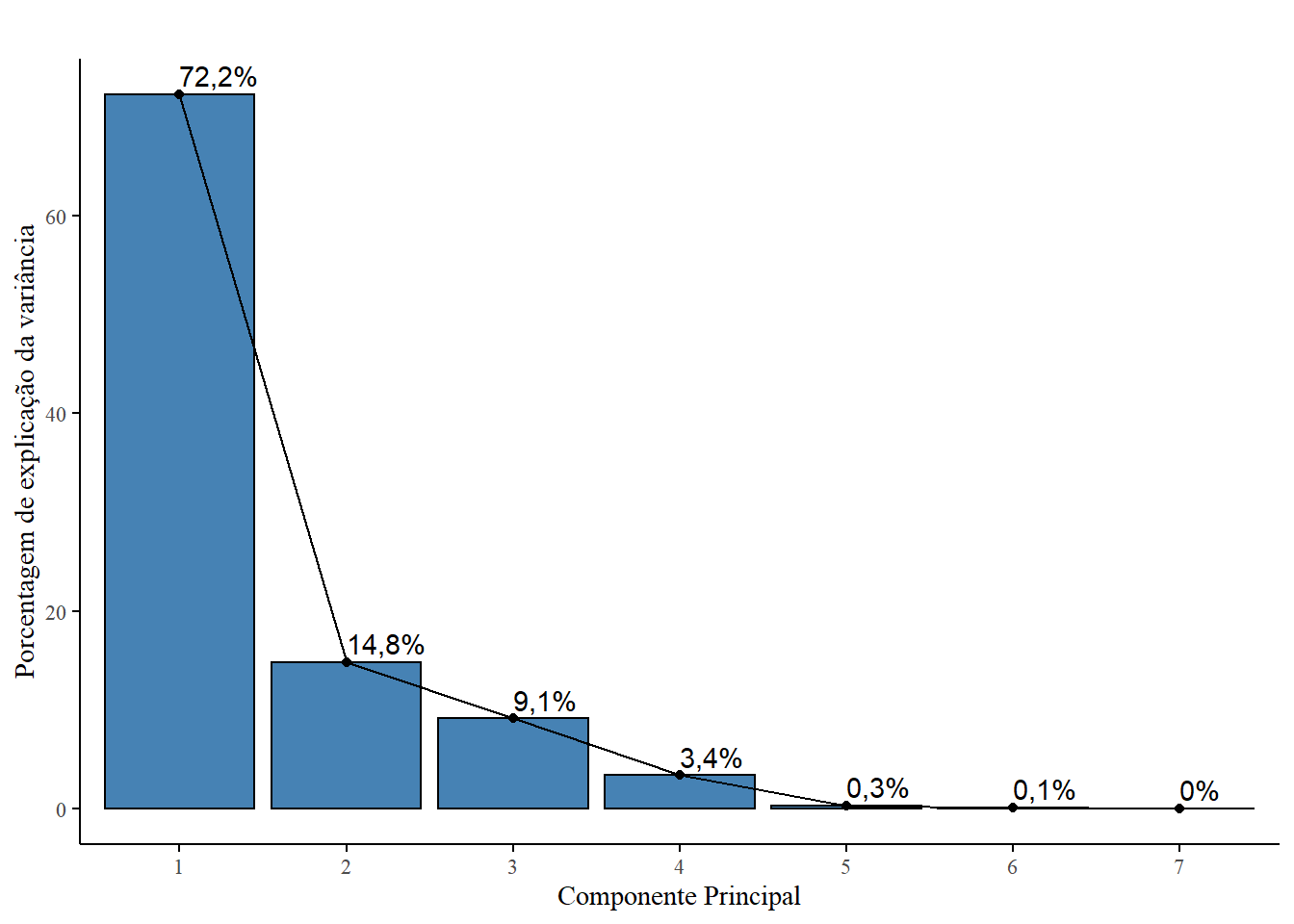
15.6 Manualmente pelo stats
15.6.1 Somente colunas
par(family="serif") # fonte times new roman
bar=barplot(pca$eig[,2],
ylim=c(0,100))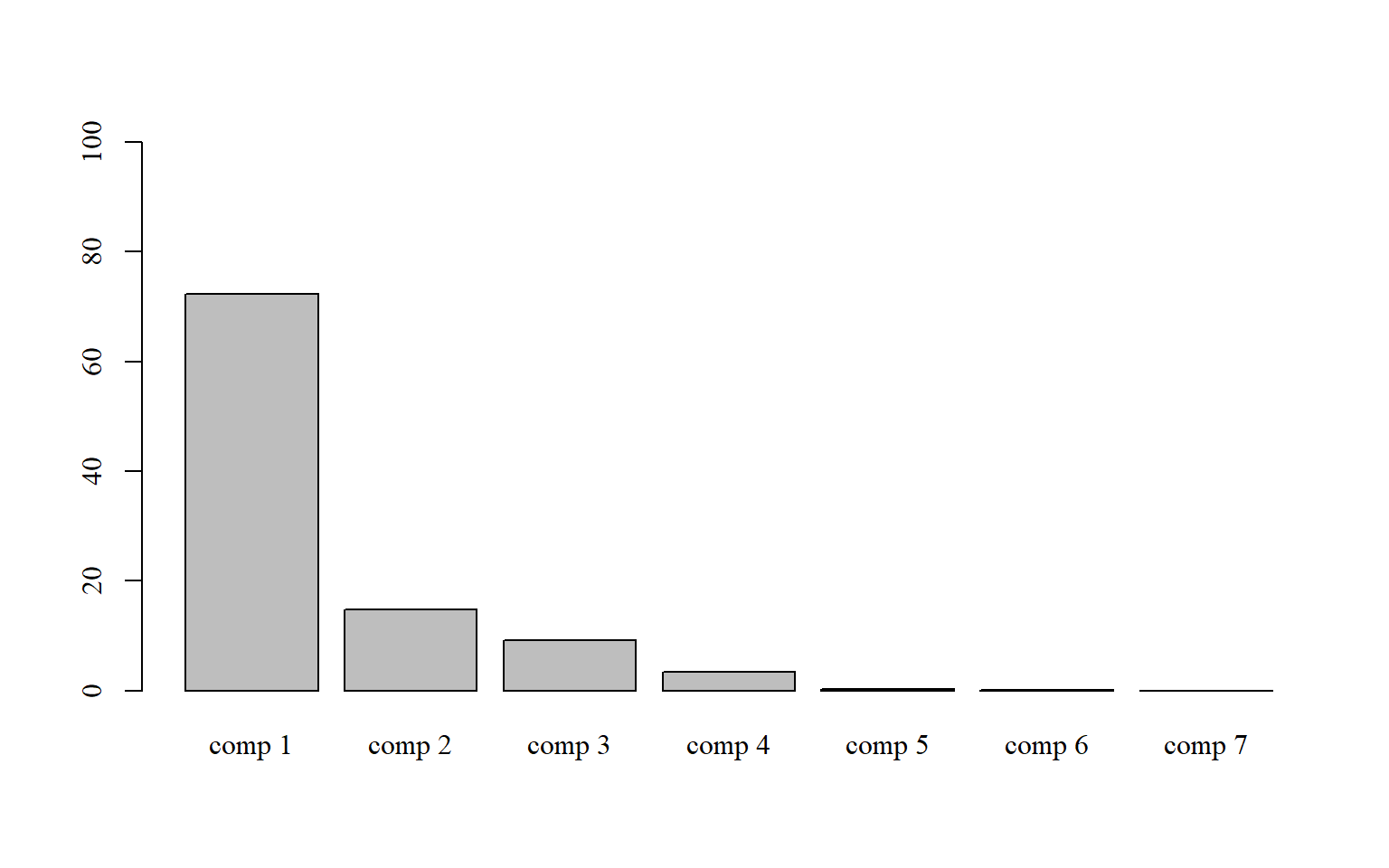
15.6.2 Com colunas, pontos e linhas
par(family="serif") # fonte times new roman
bar=barplot(pca$eig[,2],
ylim=c(0,100))
points(bar,
pca$eig[,2],
type = "o")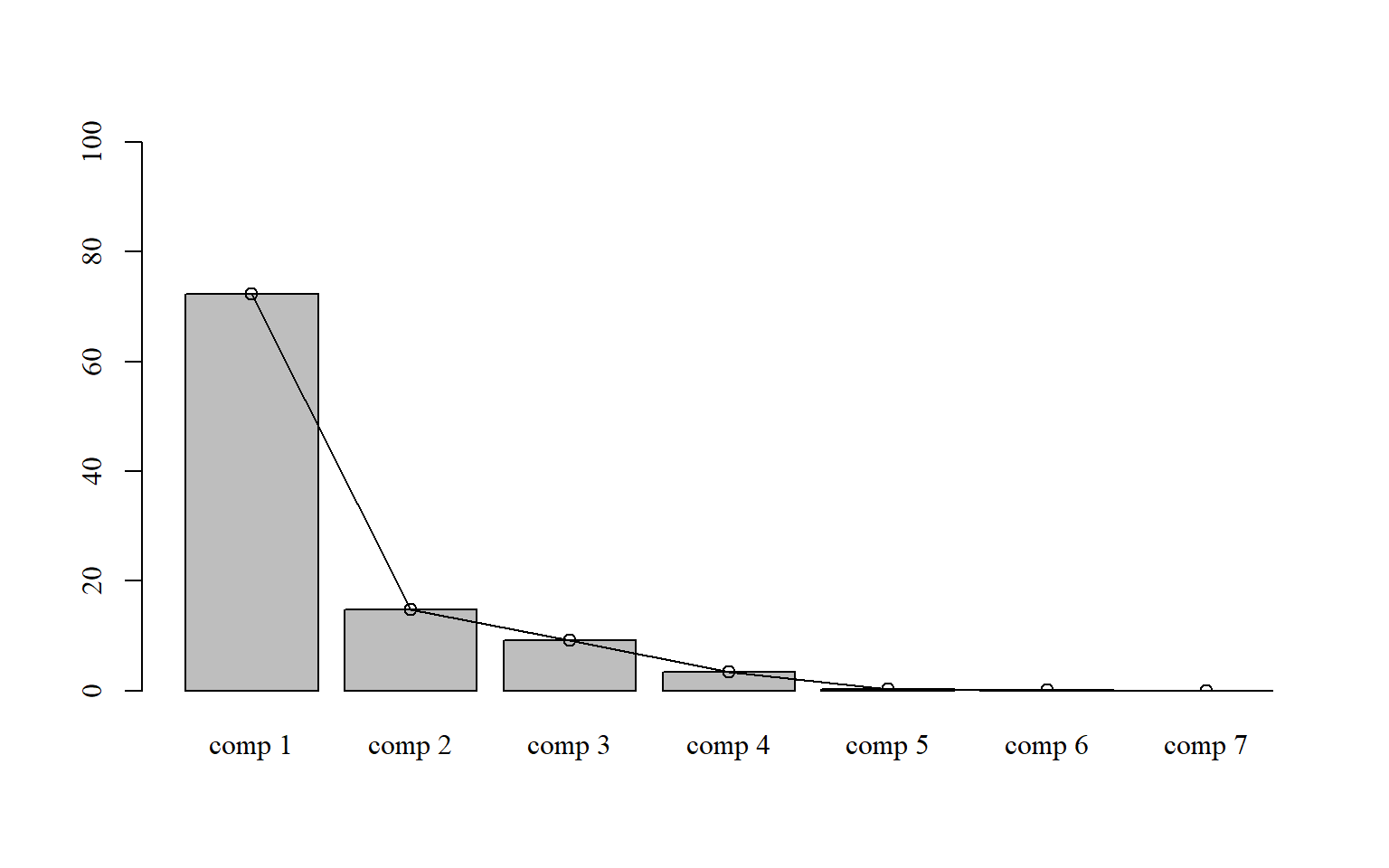
15.6.3 Com colunas, pontos, linhas e legenda
par(family="serif") # fonte times new roman
bar=barplot(pca$eig[,2],
ylim=c(0,100))
points(bar,
pca$eig[,2],
type = "o")
text(bar,
pca$eig[,2]+5,
round(pca$eig[,2],2))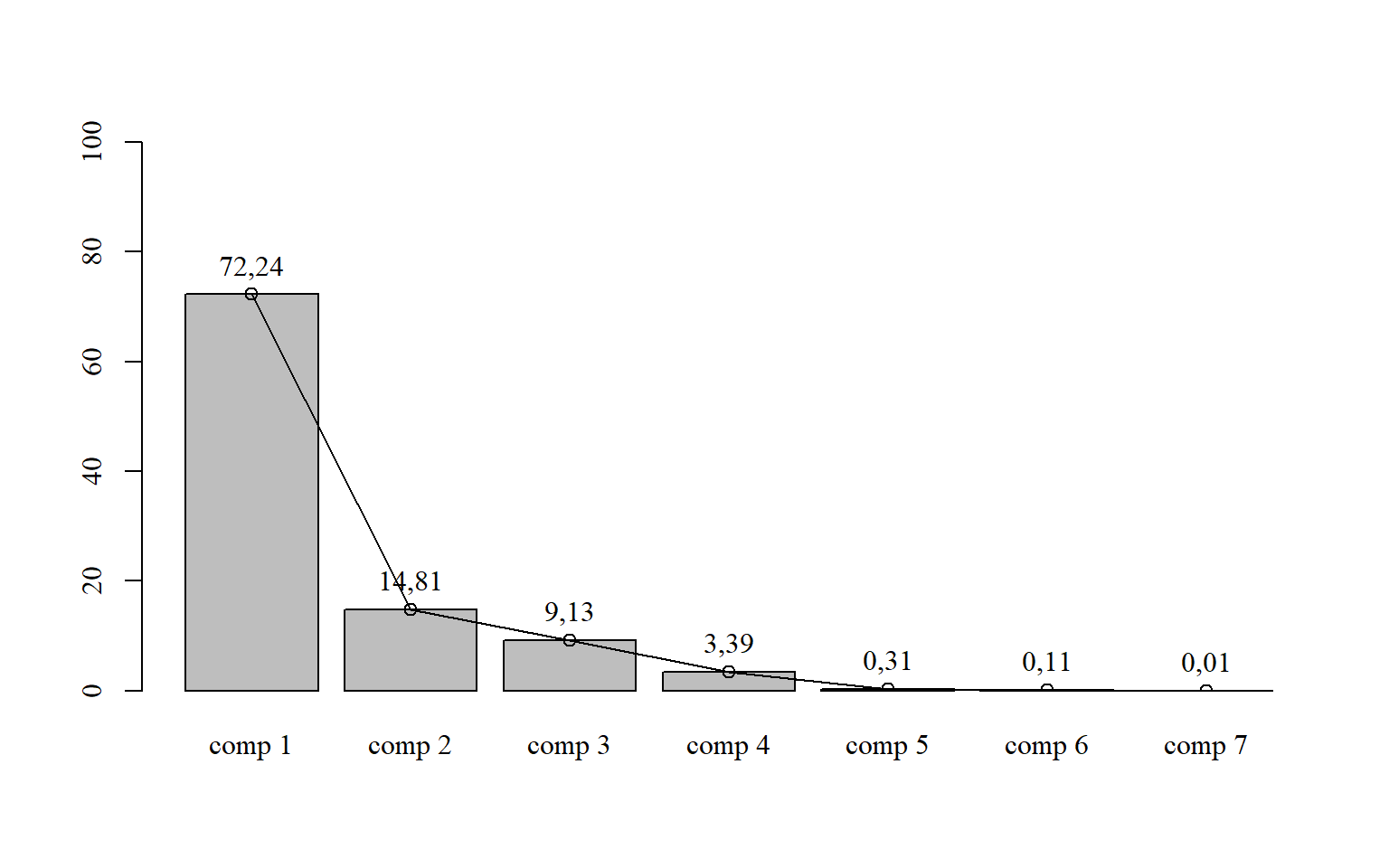
15.6.4 Editando
rownames(pca$eig)=c(paste("CP",1:length(pca$eig[,2])))
par(family="serif") # fonte times new roman
bar=barplot(pca$eig[,2],
ylim=c(0,100),
las=1,
col="darkblue",
xlab="Componente principal",
ylab="Porcentagem de explicação")
abline(h=0)
points(bar,
pca$eig[,2],
type = "o")
text(bar,
pca$eig[,2]+5,
round(pca$eig[,2],2))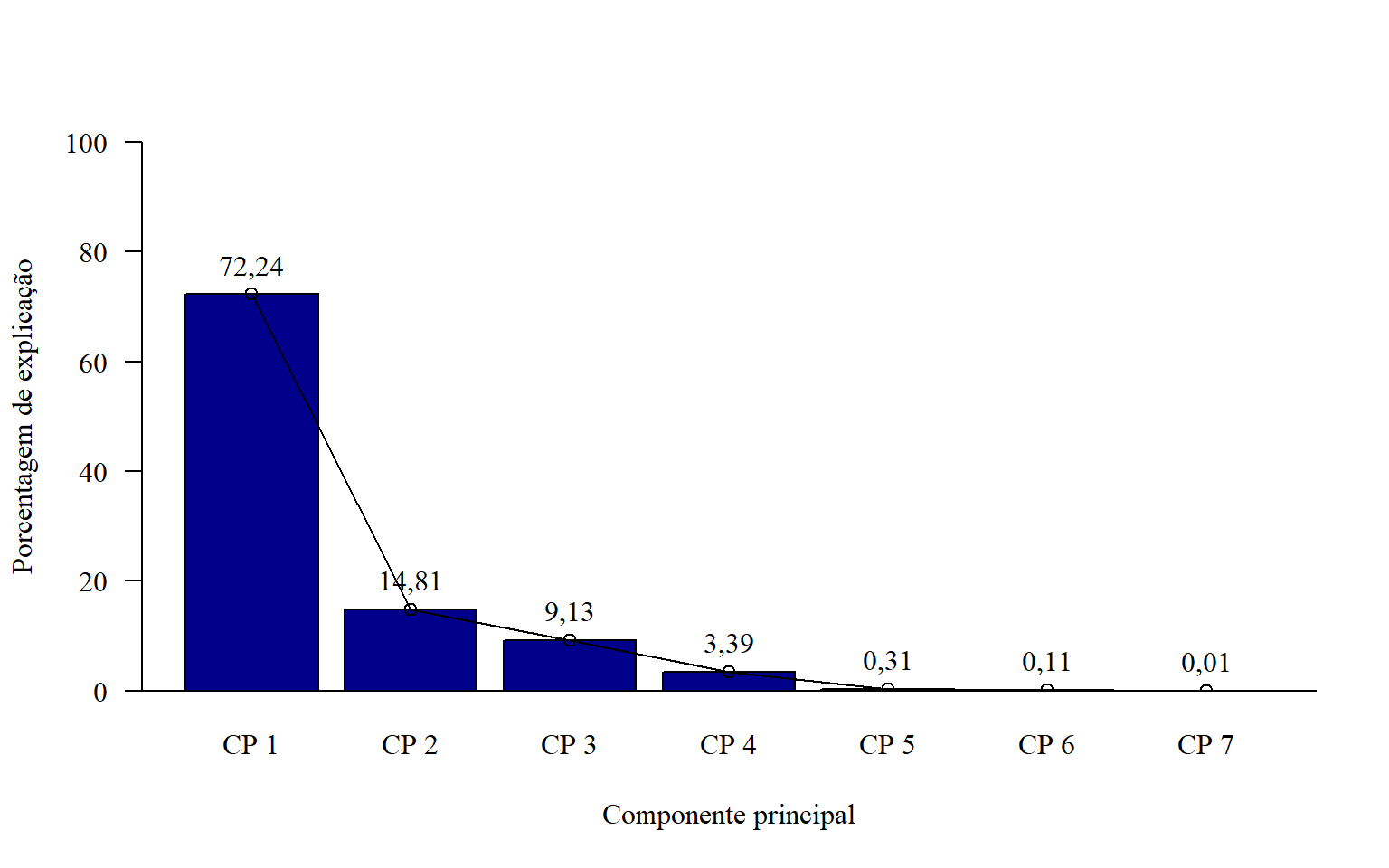
15.7 Correlação com variável latente
15.7.1 Calculando as médias
mph=tapply(ph, Trat, mean)
mHAL=tapply(HAL, Trat, mean)
mK=tapply(K, Trat, mean)
mP=tapply(P, Trat, mean)
mCa=tapply(Ca, Trat, mean)
mMg=tapply(Mg, Trat, mean)
mV=tapply(V, Trat, mean)
dadosm=data.frame(mph,mHAL,mK,mP,mCa,mMg,mV)15.8 Pacote psych
library(psych)
pca.solo <- principal(scale(dadosm), # scale é para padronizar dados
nfactors=5, # Numero de componentes
n.obs=10, # possui 10 observações/ variável
rotate='none',
scores=TRUE)
pca.solo## Principal Components Analysis
## Call: principal(r = scale(dadosm), nfactors = 5, rotate = "none", n.obs = 10,
## scores = TRUE)
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 PC3 PC4 PC5 h2 u2 com
## mph 0,95 0,26 -0,02 -0,14 0,12 1 3,1e-04 1,2
## mHAL -0,93 0,09 0,20 0,28 0,06 1 5,4e-04 1,3
## mK 0,69 0,24 0,69 -0,01 -0,02 1 7,4e-04 2,2
## mP -0,27 0,95 -0,17 0,03 -0,04 1 5,4e-05 1,2
## mCa 0,92 0,03 -0,28 0,28 0,02 1 2,9e-03 1,4
## mMg 0,96 -0,09 0,08 0,24 -0,04 1 2,9e-03 1,2
## mV 0,99 -0,01 -0,13 -0,08 -0,03 1 8,4e-04 1,1
##
## PC1 PC2 PC3 PC4 PC5
## SS loadings 5,06 1,04 0,64 0,24 0,02
## Proportion Var 0,72 0,15 0,09 0,03 0,00
## Cumulative Var 0,72 0,87 0,96 1,00 1,00
## Proportion Explained 0,72 0,15 0,09 0,03 0,00
## Cumulative Proportion 0,72 0,87 0,96 1,00 1,00
##
## Mean item complexity = 1,4
## Test of the hypothesis that 5 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0
## with the empirical chi square 0 with prob < NA
##
## Fit based upon off diagonal values = 115.8.1 Extraindo correlações
(load <- pca.solo$loadings)##
## Loadings:
## PC1 PC2 PC3 PC4 PC5
## mph 0,949 0,258 -0,137 0,116
## mHAL -0,933 0,201 0,278
## mK 0,687 0,240 0,685
## mP -0,270 0,946 -0,171
## mCa 0,918 -0,277 0,276
## mMg 0,961 0,239
## mV 0,987 -0,129
##
## PC1 PC2 PC3 PC4 PC5
## SS loadings 5,057 1,037 0,639 0,237 0,022
## Proportion Var 0,722 0,148 0,091 0,034 0,003
## Cumulative Var 0,722 0,871 0,962 0,996 0,99915.8.2 Correlação com a variável latente CP1
library(lattice)
sorted.loadings1 <- load[order(load[,1]),1]
(load1 <- dotplot(sorted.loadings1,
cex=1.5,
xlab="Correlação com a variável latente",
col="black",
scales=list(fontfamily="serif",cex=1.2),
auto.key=list(cex=1.2),
pch=16))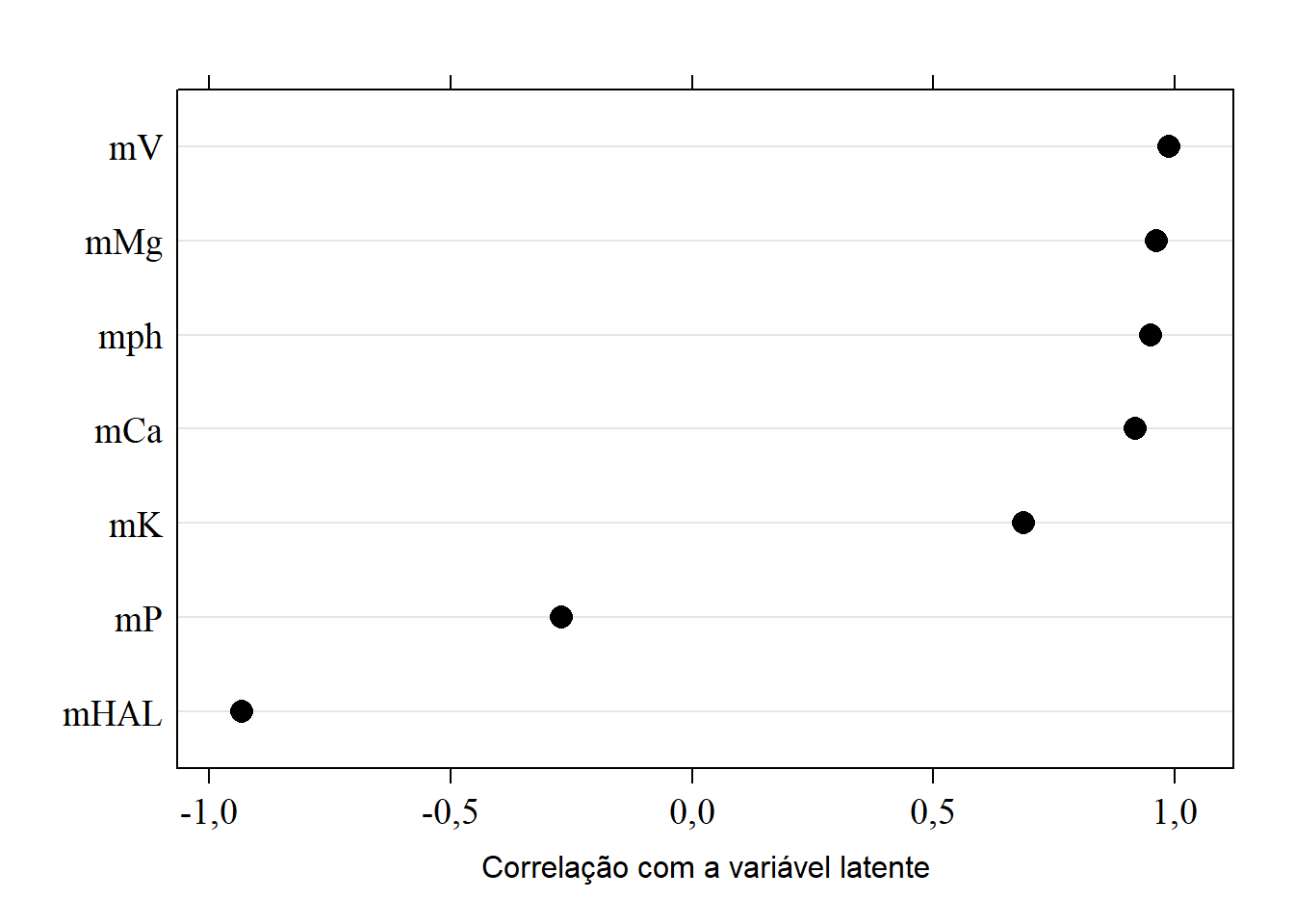
15.8.3 Correlação com a variável latente CP2
sorted.loadings2 <- load[order(load[,2]),2]
(load2 <- dotplot(sorted.loadings2,
cex=1.5,
xlab="Correlação com a variável latente",
col="black",
scales=list(fontfamily="serif",cex=1.2),
pch=16))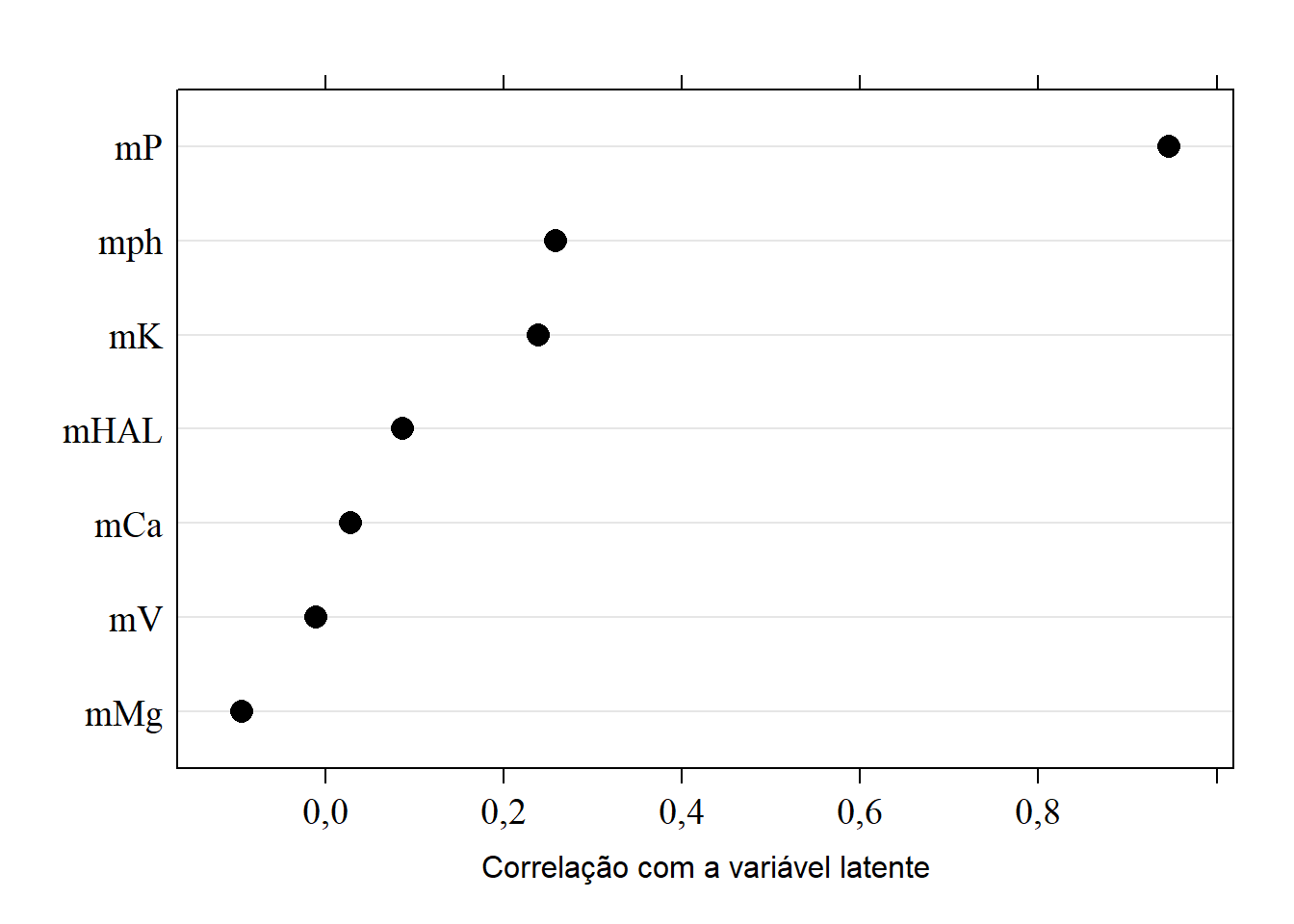
15.8.4 Correlação com a variável latente CP3
sorted.loadings3 <- load[order(load[,3]),3]
(load3 <- dotplot(sorted.loadings3,
cex=1.5,
xlab="Correlação com a variável latente",
col="black",
scales=list(fontfamily="serif",cex=1.2),
pch=16))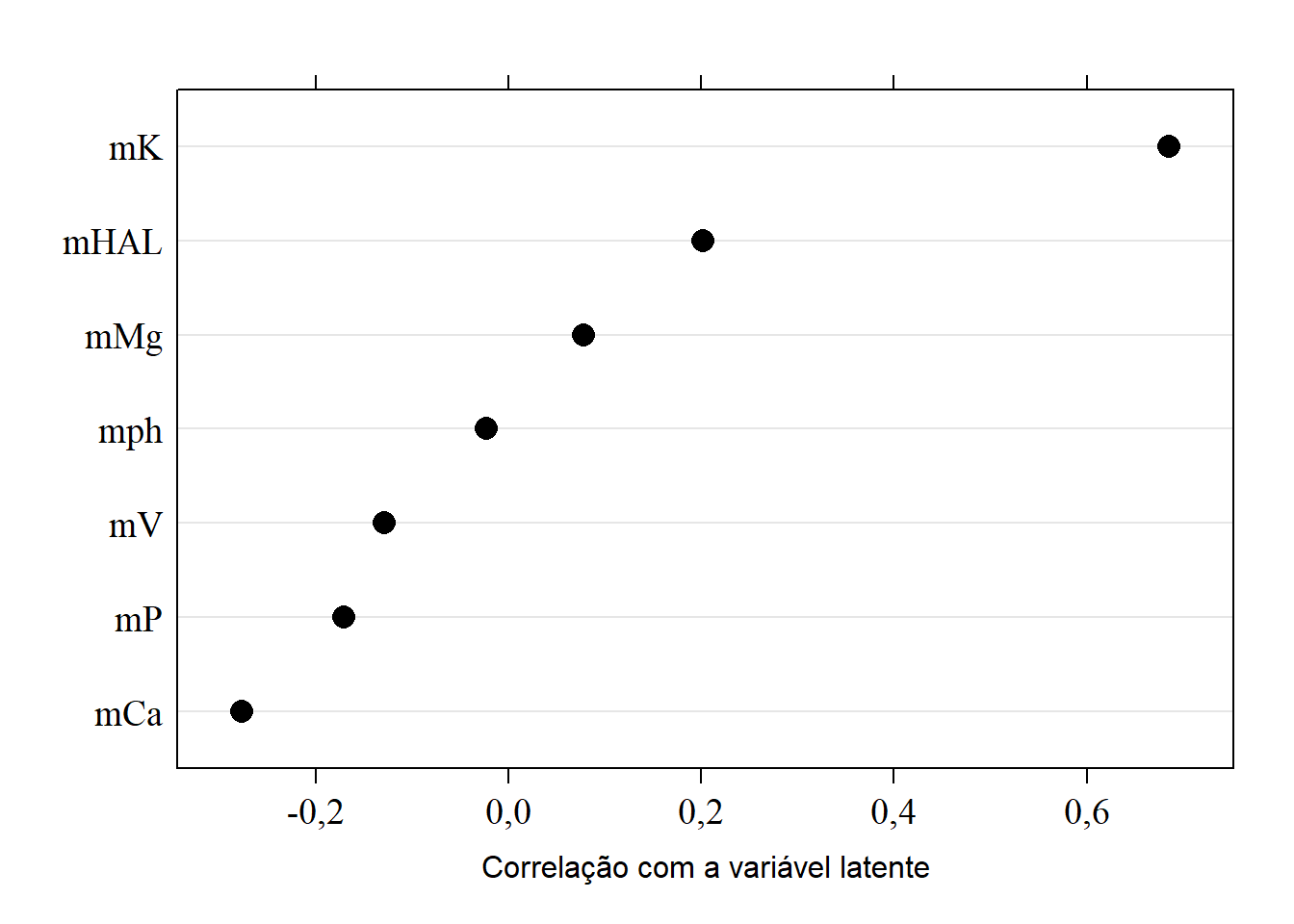
15.9 Extraindo cluster de forma automática
15.9.1 Conjunto de dados
var1=c(rnorm(20,10,2),rnorm(20,20,2),rnorm(20,15,2))
var2=c(rnorm(20,20,2),rnorm(20,18,2),rnorm(20,15,2))
var3=c(rnorm(20,100,2),rnorm(20,60,2),rnorm(20,80,2))
var4=c(rnorm(20,150,2),rnorm(20,160,2),rnorm(20,140,2))
trat=paste("T",1:60)
dados=data.frame(trat,var1,var2,var3,var4)15.9.2 Construindo Dendrograma
Obs. método UPGMA - average
dend=as.dendrogram(hclust(dist(scale(dados[,2:5])),method = "average"))
library(dendextend)
dend=set(dend,
"branches_k_color",
value = 1:3,
k = 3)15.9.3 Extraindo cluster
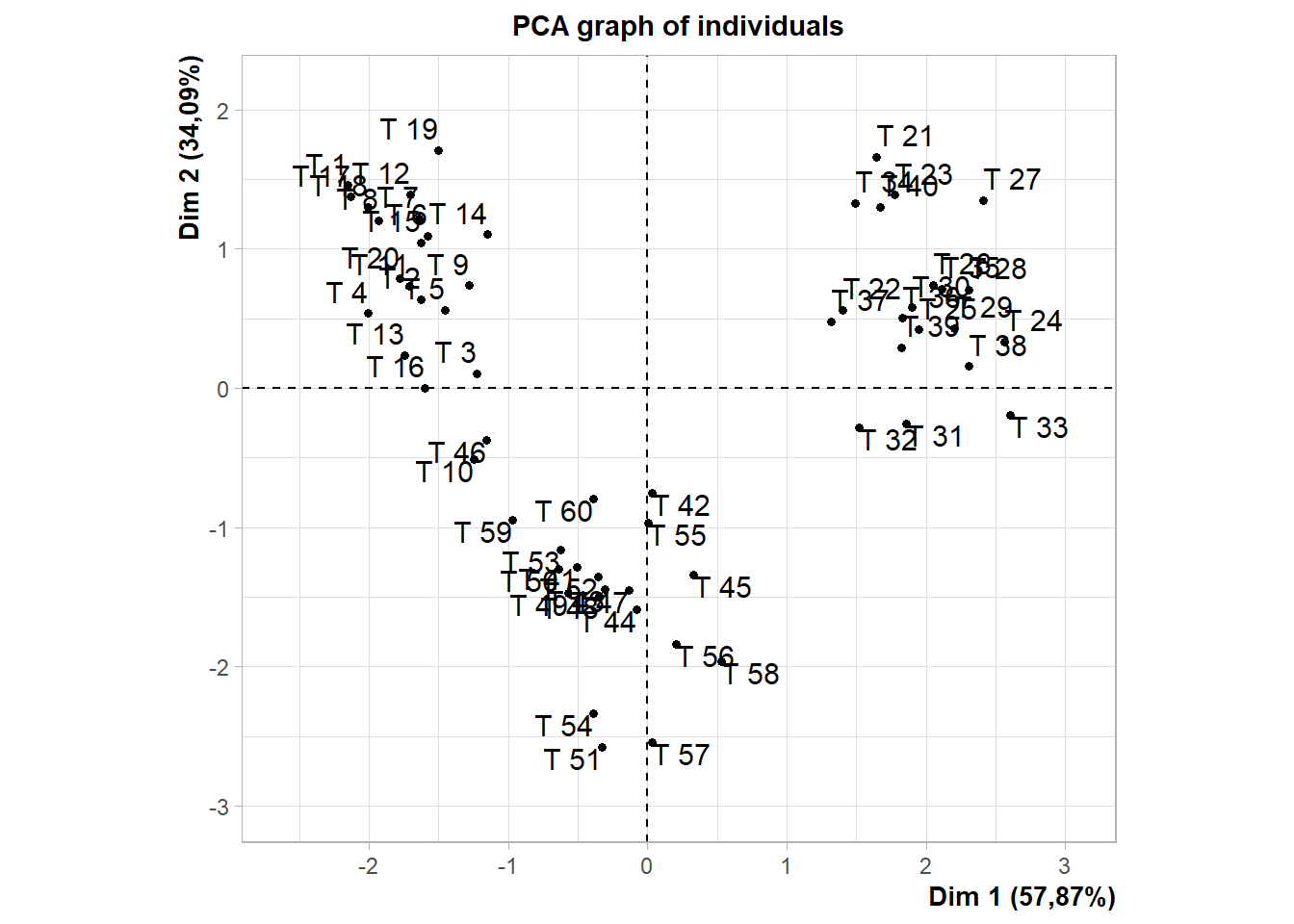
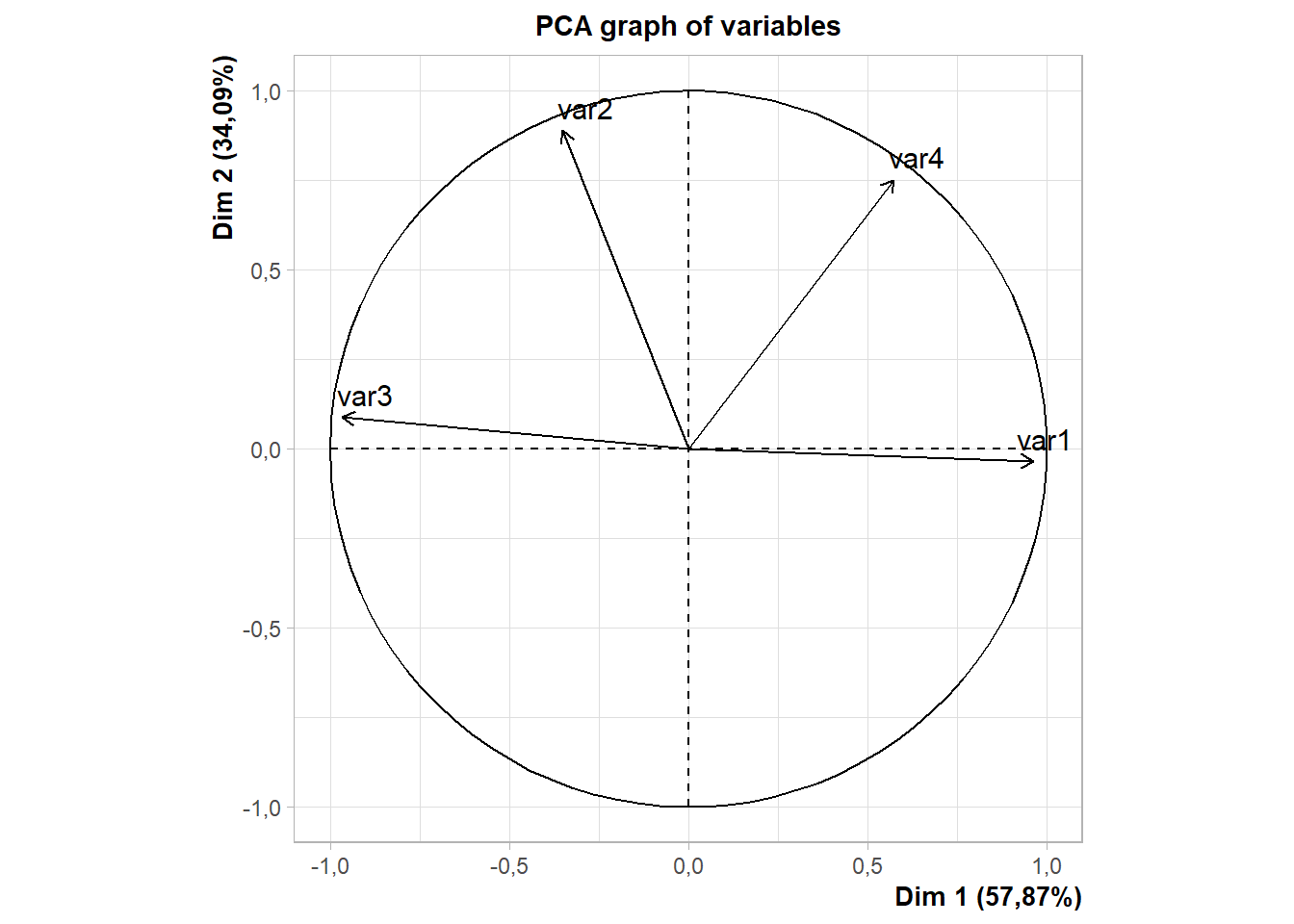
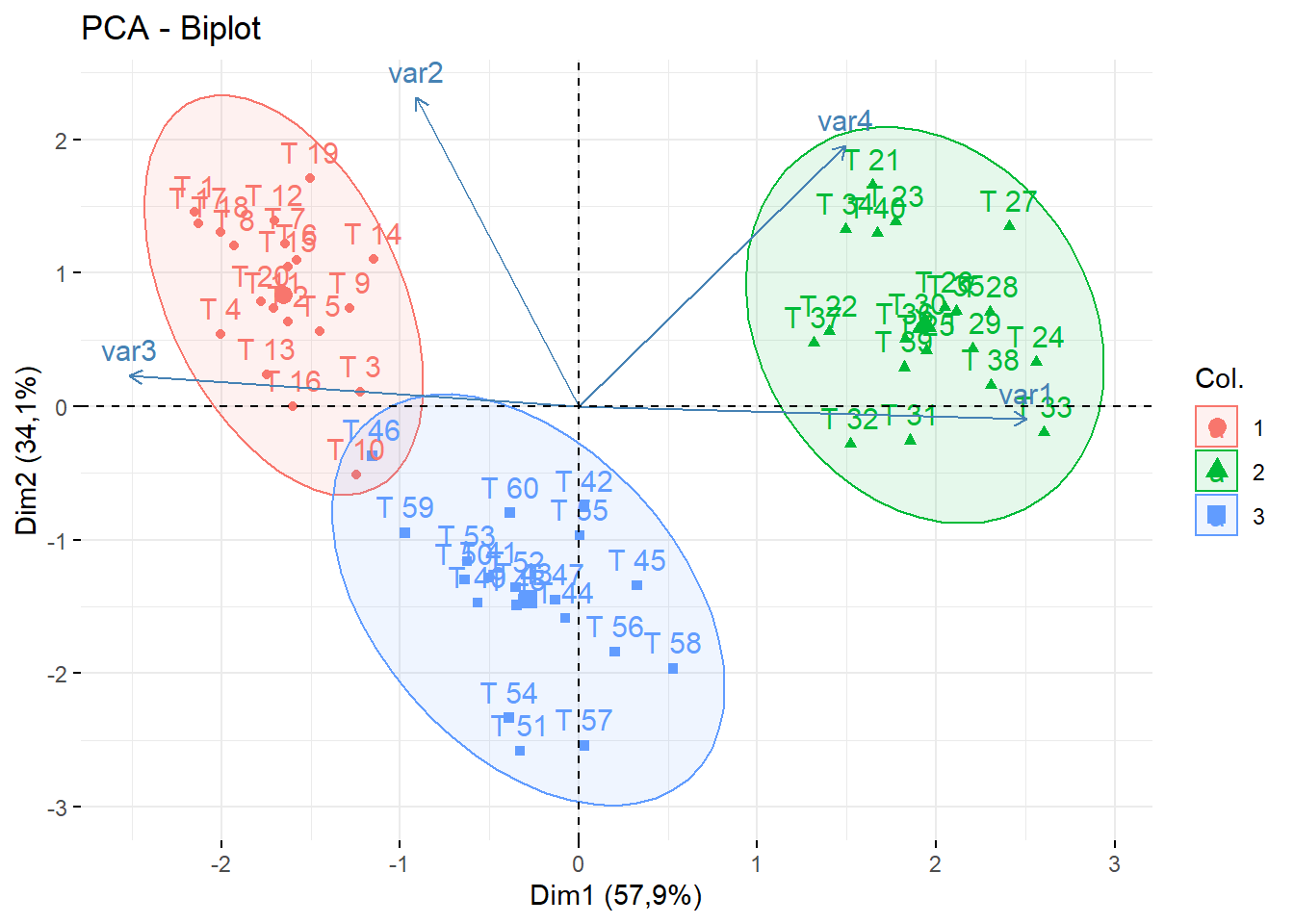
cluster=as.factor(as.vector(cutree(dend,k=3)))15.9.4 PCA
Obs. Não editado
library(factoextra);library(FactoMineR)
data=dados[,2:5]
rownames(data)=dados$trat
fviz_pca_biplot(PCA(data),col.ind = cluster, addEllipses = T) # default e padronizado