14 Delineamento em Blocos Casualizados
- O delineamento em blocos ao acaso ou o delineamento em blocos casualizados são aqueles que levam em consideração os 3 princípios básicos da experimentação;
- O controle local é feito na sua forma mais simples e é chamado de blocos;
- Sempre que não houver homogeneidade das condições experimentais, deve-se utilizar o princípio do controle local;
- Estabelece-se, então, sub-ambientes homogêneos (blocos) e instalando, em cada um deles, todos os tratamentos, igualmente repetidos;
- Nessas condições, o delineamento em blocos casualizados é mais eficiente que o inteiramente ao acaso e, essa eficiência depende da uniformidade das parcelas de cada bloco;
- Pode-se haver diferenças bem acentuadas de um bloco para outro.
- O número de blocos e de repetições coincide apenas quando os tratamentos ocorrem uma única vez em cada bloco.
14.1 Vantagens
- Controla as diferenças que ocorrem nas condições ambientais, de um bloco para outro;
- Conduz a uma estimativa mais exata para a variância residual, uma vez que a variação ambiental entre blocos é isolada.
14.2 Desvantagens
- Pela utilização do princípio do controle local, há uma redução no número de graus de liberdade do resíduo;
- Exigência de homogeneidade das parcelas dentro de cada bloco limita o número de tratamentos, que não pode ser muito elevado.
14.3 Modelo matemático
\[\begin{eqnarray} y_{ji}=\mu+\tau_i+\beta_j+\varepsilon_{ij} \end{eqnarray}\]
\(y_{ji}\): é a observação referente ao tratamento i no bloco j;
\(\mu\): é a média geral (ou constante comum a todas as observações);
\(\tau_i\): é o efeito de tratamento, com \(i = 1, 2, . . . , I\);
\(\beta_j\): é o efeito do bloco;
\(\varepsilon_{ij}\): é o erro experimental, tal que \(\varepsilon_{ij}\)~N(0; \(\sigma^2\)).
14.4 Hipóteses e Modelo
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 =\mu_i\\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
| CV | G.L. | S.Q. | Q.M. | Fcalc | Ftab |
|---|---|---|---|---|---|
| Tratamentos | \(a - 1\) | \(SQ_{Trat}\) | \(\frac{SQ_{Trat}}{a-1}\) | \(\frac{QMTrat}{QMRes}\) | \(F(\alpha;GL_{Trat} ;GL_{Res})\) |
| Blocos | \(b-1\) | \(Sq_{Blocos}\) | \(\frac{SQ_{Blocos}}{b-1}\) | \(\frac{QM_{bloco}}{QM_{Res}}\) | \(F(\alpha;GL_{bloco} ;GL_{Res})\) |
| resíduo | \((a-1)(b-1)\) | \(SQ_{Res}\) | \(\frac{SQRes}{(a-1)(b-1)}\) | - | |
| Total | \(ab-1\) | \(SQ_{Total}\) | - | - |
14.5 Croqui
Criando uma função para fazer um croqui (Bloco em coluna)
# Não alterar os comandos da função
library(agricolae)
library(gridExtra)
library(grid)
croqui=function(trat,r){
sort=design.rcbd(trat,r,serie=0)
sort$book[,3]=as.factor(matrix(sort$book[,3],r,,T))
ncol=r
gs <- lapply(sort$book[,3], function(ii)
grobTree(rectGrob(gp=gpar(fill=ii, alpha=0.5)),textGrob(ii)))
grid.arrange(grobs=gs, ncol=ncol)}Vetor de tratamentos
trat=c("T1","T2","T3","T4")Usando a função
croqui(trat,r=3)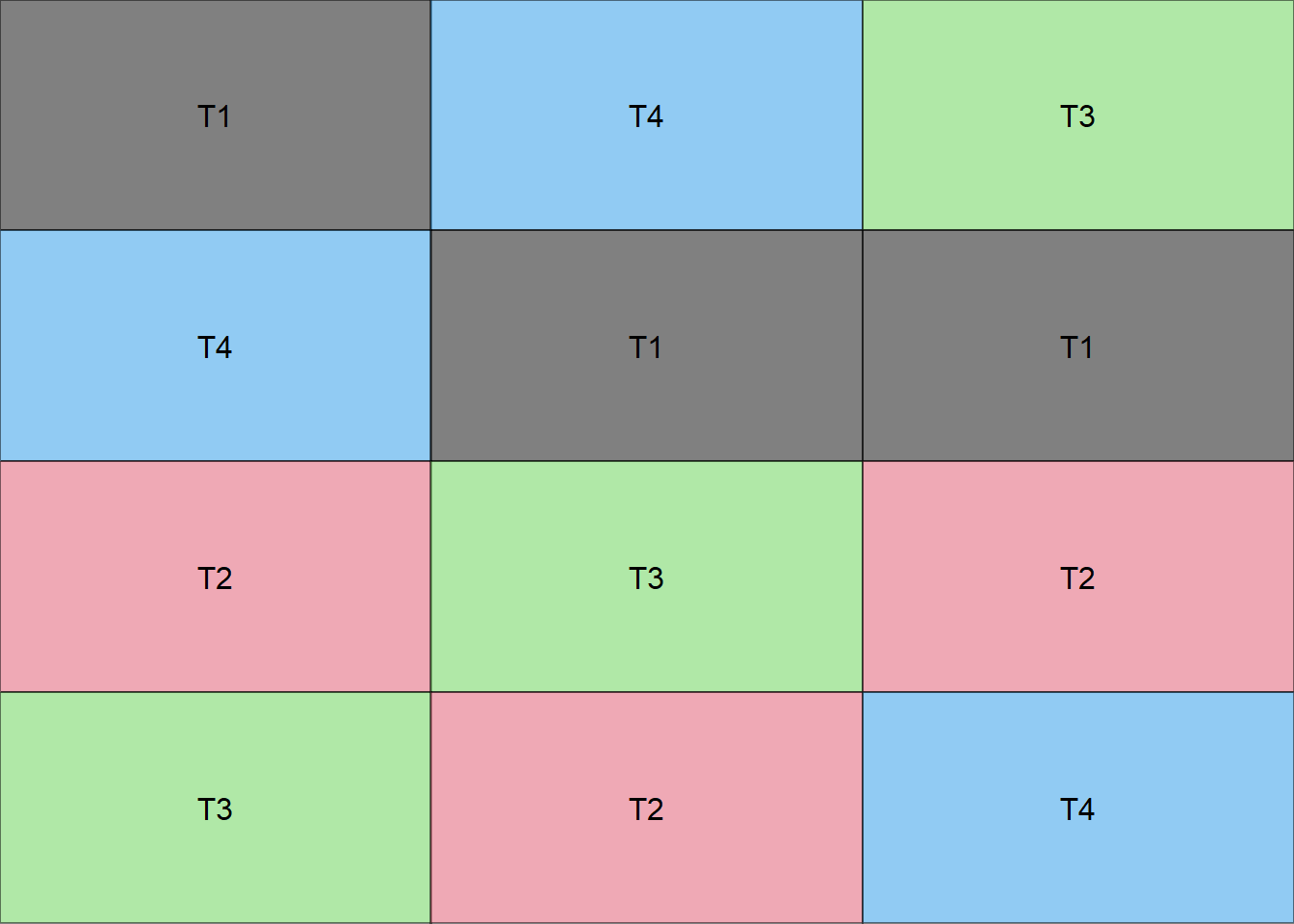
Criando uma função para fazer um croqui (Bloco em linha)
# Não alterar os comandos da função
library(agricolae)
library(gridExtra)
library(grid)
croqui=function(trat,r){
sort=design.rcbd(trat,r,serie=0)
sort$book[,3]=as.factor(t(matrix(sort$book[,3],r,,T)))
ncol=length(levels(sort$book[,3]))
gs <- lapply(sort$book[,3], function(ii)
grobTree(rectGrob(gp=gpar(fill=ii, alpha=0.5)),textGrob(ii)))
grid.arrange(grobs=gs, ncol=ncol)}Vetor de tratamentos
trat=c("T1","T2","T3","T4")Usando a função
croqui(trat,r=3)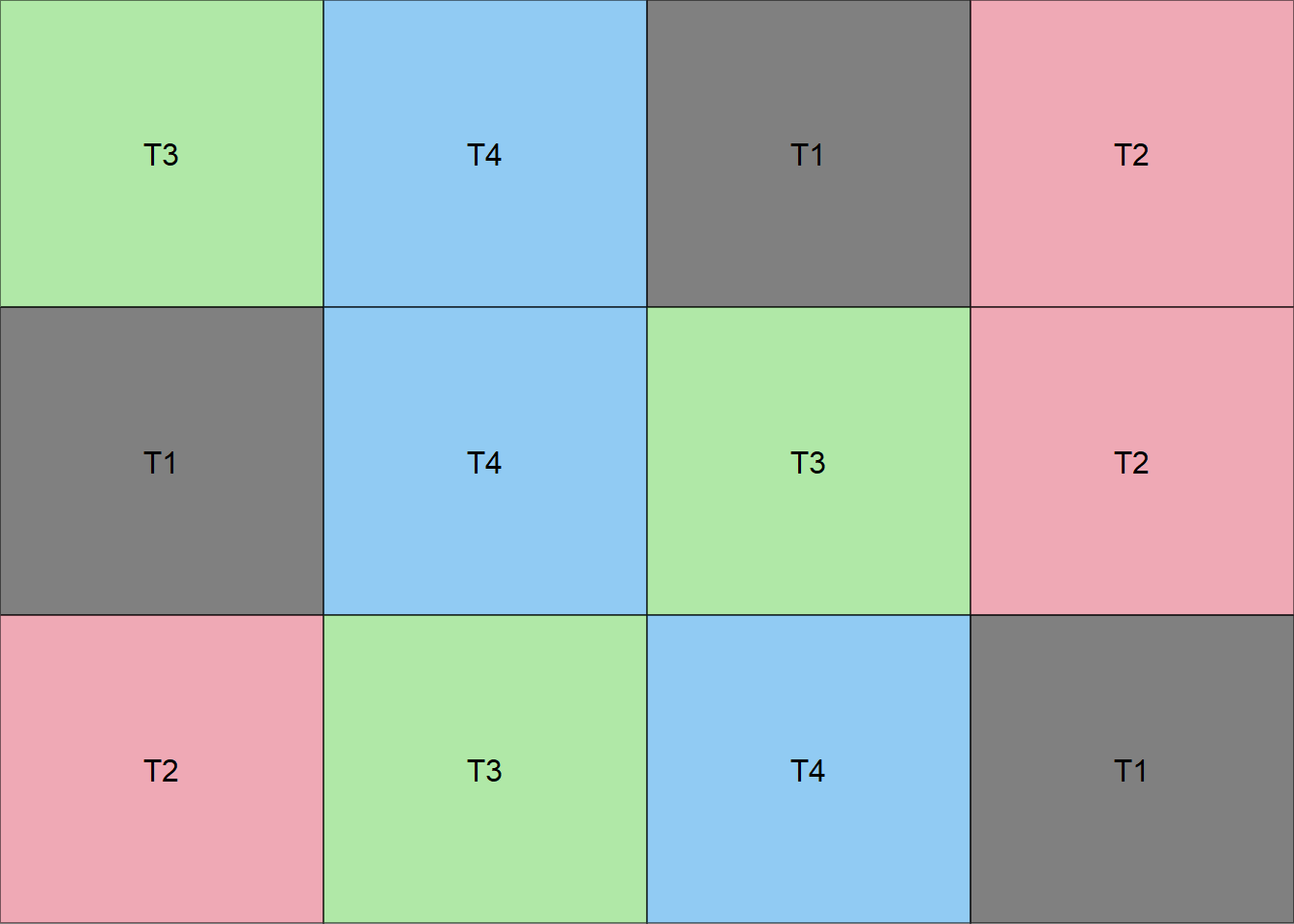
14.6 Exemplo 1
Exemplo do Livro Planejamento e Análise Estatística de Experimentos Agronômicos (2013) - Décio Barbin - pg. 72

Um experimento foi conduzido com o objetivo de estudar o comportamento de nove porta-enxertos para a laranjeira Valência.
Os porta-enxertos são:
- T1: Tangerina Sunki
- T2: Limão rugoso Nacional
- T3: Limão rugoso da Flórida
- T4: Tangerina Cleópatra
- T5: Citranger-troyer
- T6: Trifoliata
- T7: Tangerina Cravo
- T8: Laranja caipira
- T9: Limão Cravo
Delineamento experimental: Blocos casualizados.
Repetições/Tratamento: 3 repetições
Croqui experimental é apresentado abaixo:
| Bloco | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| B1 | T3 | T1 | T4 | T8 | T6 | T7 | T2 | T9 | T5 |
| B2 | T7 | T3 | T9 | T4 | T2 | T5 | T1 | T6 | T8 |
| B3 | T8 | T6 | T2 | T1 | T7 | T9 | T3 | T4 | T5 |
Para o ano de 1973 (Plantas com 12 anos de idade), os resultados de produção, em número médio de frutos por planta, foram:
| Tratamentos | B1 | B2 | B3 | Total |
|---|---|---|---|---|
| 1 | 145 | 155 | 166 | 466 |
| 2 | 200 | 190 | 190 | 580 |
| 3 | 183 | 186 | 208 | 577 |
| 4 | 190 | 175 | 186 | 551 |
| 5 | 180 | 160 | 156 | 496 |
| 6 | 130 | 160 | 130 | 420 |
| 7 | 206 | 165 | 170 | 541 |
| 8 | 250 | 271 | 230 | 751 |
| 9 | 164 | 190 | 193 | 547 |
| Total | 1648 | 1652 | 1629 | 4929 |
14.6.1 Conjunto de dados
resposta=c(145,155,166,
200,190,190,
183,186,208,
190,175,186,
180,160,156,
130,160,130,
206,165,170,
250,271,230,
164,190,193)
cultivar=rep(c(paste("T",1:9)),e=3)
cultivar=as.factor(cultivar)
bloco=as.factor(rep(c(paste("B",1:3)),9))14.7 Gráficos exploratórios
14.7.1 Gráfico de caixas
car::Boxplot(resposta~cultivar)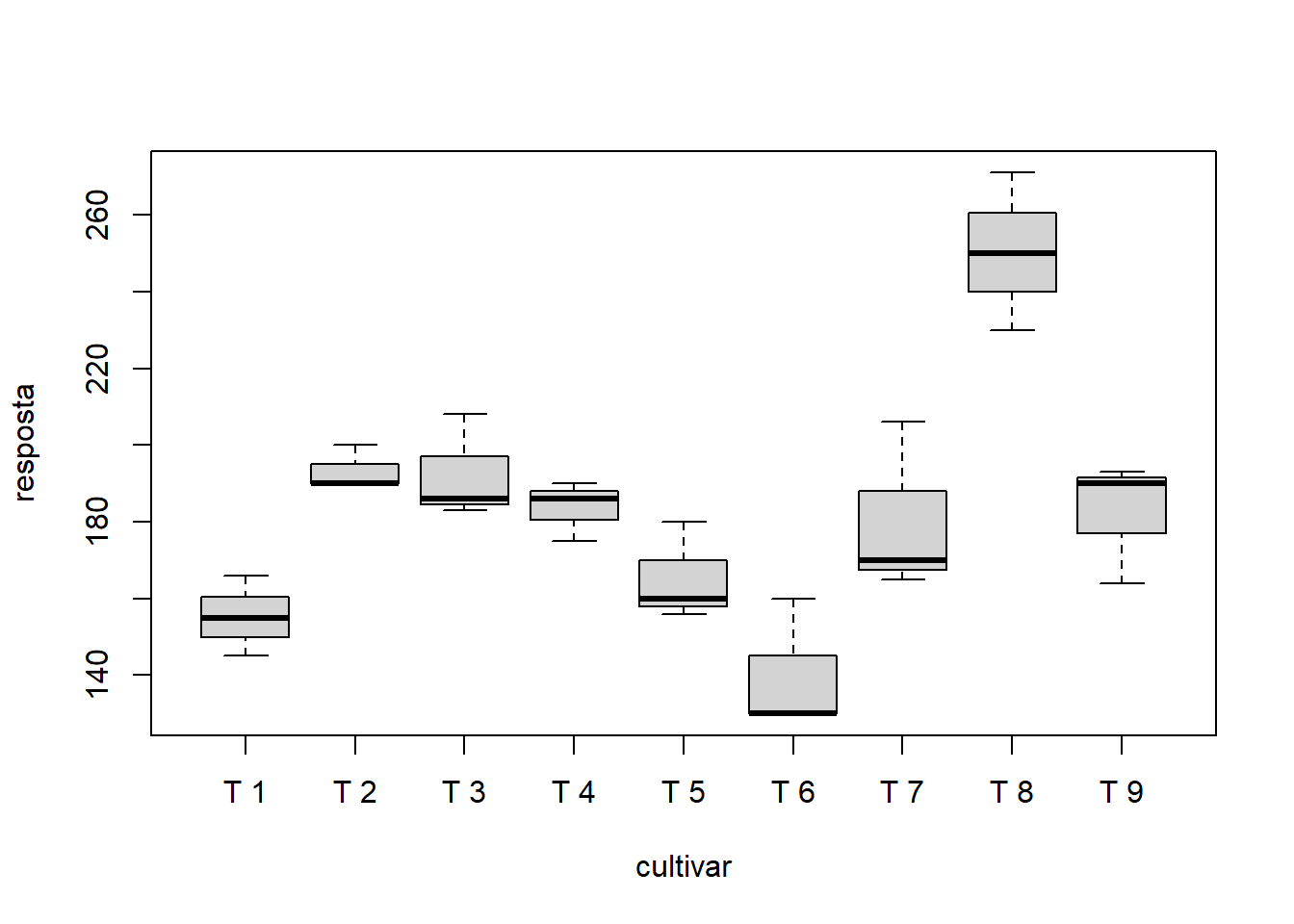
14.7.2 Histograma
hist(resposta)
14.8 Análise de variância
modelo=aov(resposta~cultivar+bloco)
anova(modelo) # Conferir GL## Analysis of Variance Table
##
## Response: resposta
## Df Sum Sq Mean Sq F value Pr(>F)
## cultivar 8 22981.3 2872.67 11.4114 2.637e-05 ***
## bloco 2 33.6 16.78 0.0666 0.9358
## Residuals 16 4027.8 251.74
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 114.9 Pressuposições
14.9.1 Normalidade dos erros
shapiro.test(modelo$residuals)##
## Shapiro-Wilk normality test
##
## data: modelo$residuals
## W = 0.94759, p-value = 0.1873Os erros seguem distribuição normal
14.9.2 Homogeneidade das variâncias
bartlett.test(modelo$residuals~cultivar)##
## Bartlett test of homogeneity of variances
##
## data: modelo$residuals by cultivar
## Bartlett's K-squared = 4.0369, df = 8, p-value = 0.8538As variâncias são homogêneas
14.9.3 Independência dos erros
lmtest::dwtest(modelo)##
## Durbin-Watson test
##
## data: modelo
## DW = 2.3246, p-value = 0.2484
## alternative hypothesis: true autocorrelation is greater than 0Os erros são independentes.
14.9.4 Teste de Aditividade de Tukey
library(asbio)
tukey.add.test(resposta,cultivar,bloco)##
## Tukey's one df test for additivity
## F = 0.6866169 Denom df = 15 p-value = 0.420307614.9.5 Gráfico de resíduos padronizados
a=anova(modelo)
plot(modelo$residuals/sqrt(a$`Mean Sq`[3]), ylab="Resíduos Padronizados")
abline(h=0)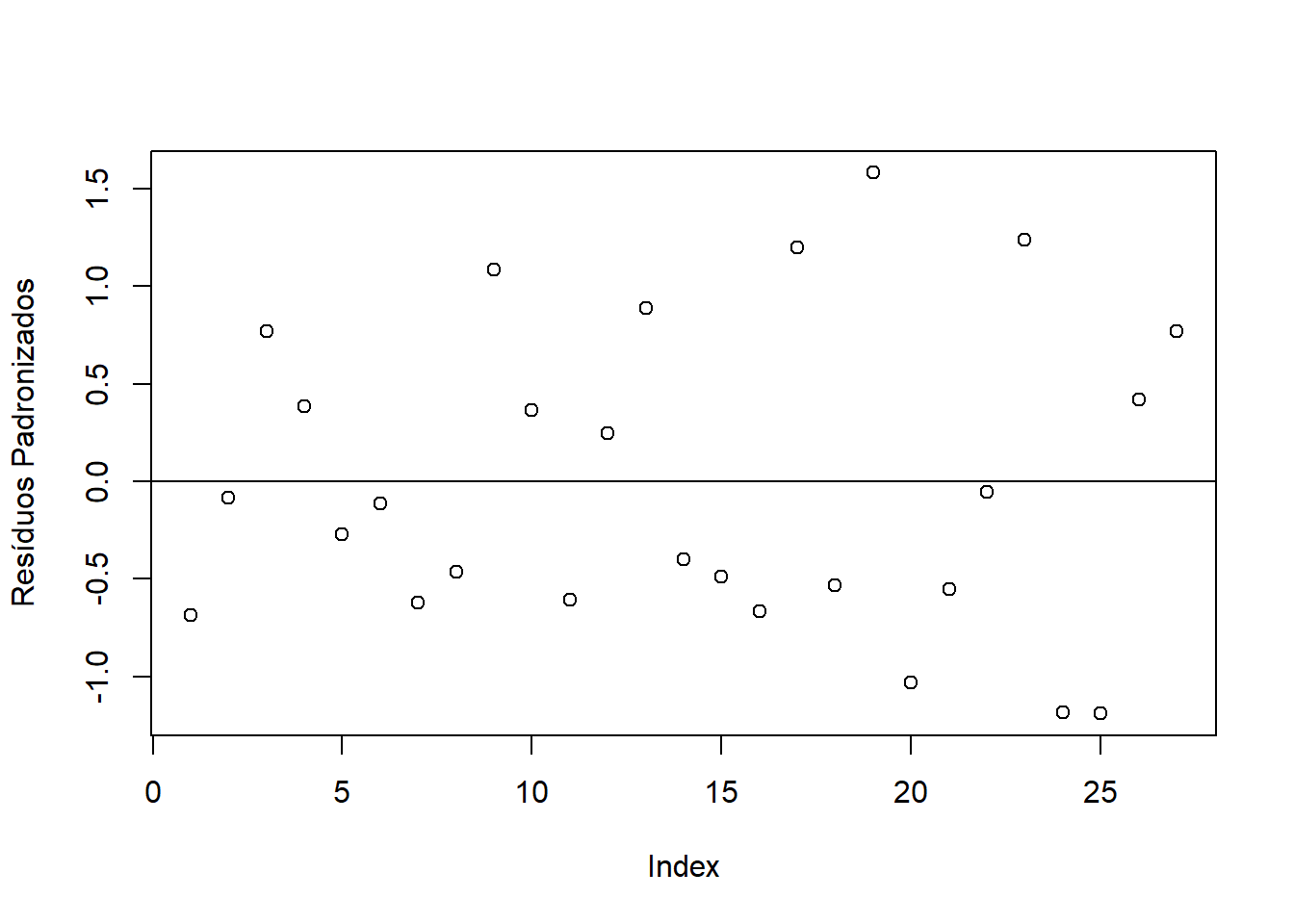
14.10 Comparação múltipla
14.10.1 Teste de Comparação Múltipla de Tukey (Utilizando o multcomp)
library(multcomp)
mcomp=glht(modelo, mcp(cultivar="Tukey"))
plot(mcomp)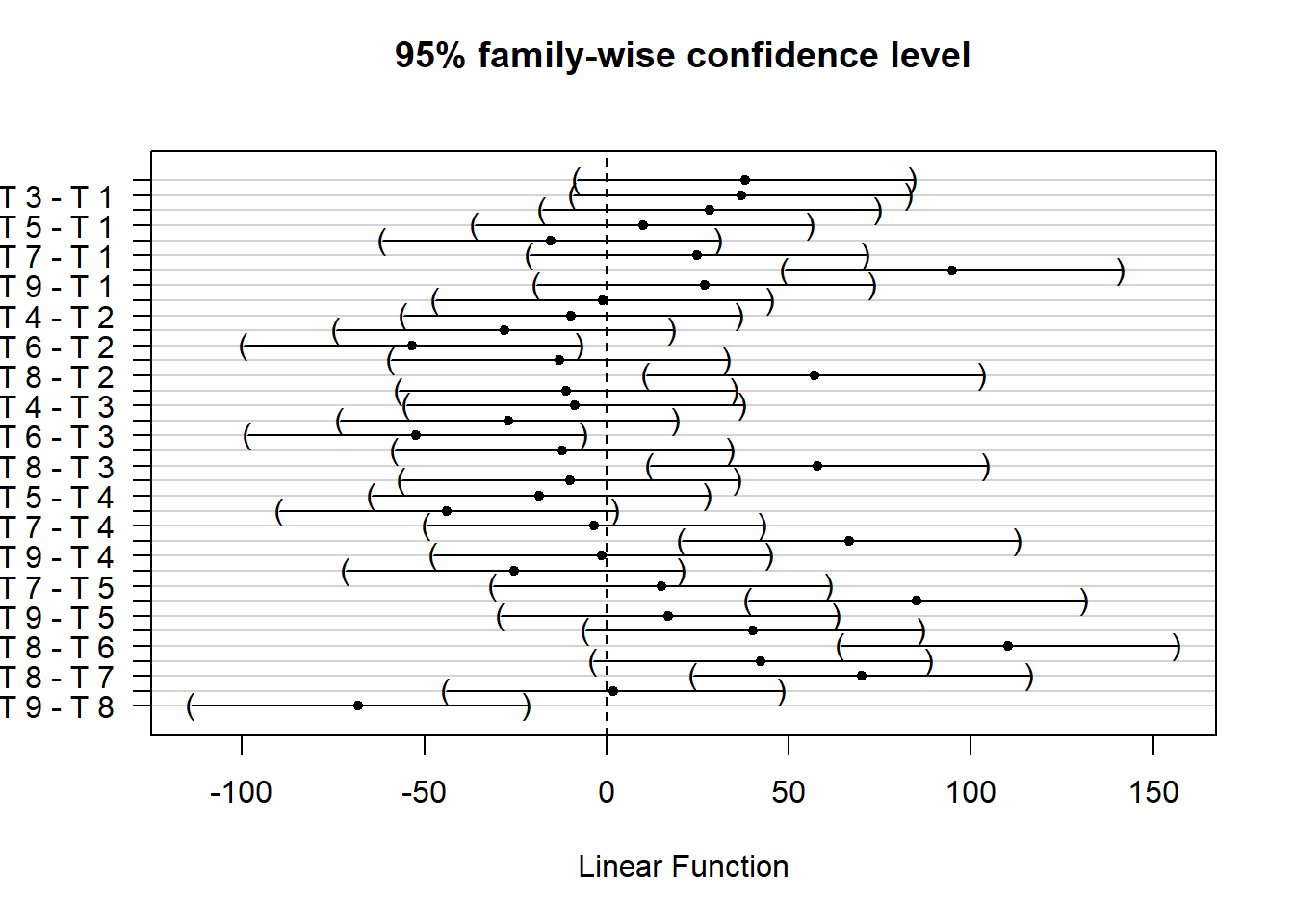
cld(mcomp)## T 1 T 2 T 3 T 4 T 5 T 6 T 7 T 8 T 9
## "ab" "b" "b" "ab" "ab" "a" "ab" "c" "ab"14.10.2 Teste de Comparação Múltipla de Tukey (Utilizando o TukeyHSD do R)
(tukey=TukeyHSD(modelo))## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = resposta ~ cultivar + bloco)
##
## $cultivar
## diff lwr upr p adj
## T 2-T 1 38.000000 -8.085796 84.085796 0.1520249
## T 3-T 1 37.000000 -9.085796 83.085796 0.1728150
## T 4-T 1 28.333333 -17.752463 74.419129 0.4559717
## T 5-T 1 10.000000 -36.085796 56.085796 0.9962223
## T 6-T 1 -15.333333 -61.419129 30.752463 0.9489958
## T 7-T 1 25.000000 -21.085796 71.085796 0.6053536
## T 8-T 1 95.000000 48.914204 141.085796 0.0000460
## T 9-T 1 27.000000 -19.085796 73.085796 0.5143733
## T 3-T 2 -1.000000 -47.085796 45.085796 1.0000000
## T 4-T 2 -9.666667 -55.752463 36.419129 0.9969942
## T 5-T 2 -28.000000 -74.085796 18.085796 0.4703201
## T 6-T 2 -53.333333 -99.419129 -7.247537 0.0172692
## T 7-T 2 -13.000000 -59.085796 33.085796 0.9799785
## T 8-T 2 57.000000 10.914204 103.085796 0.0099947
## T 9-T 2 -11.000000 -57.085796 35.085796 0.9929220
## T 4-T 3 -8.666667 -54.752463 37.419129 0.9985839
## T 5-T 3 -27.000000 -73.085796 19.085796 0.5143733
## T 6-T 3 -52.333333 -98.419129 -6.247537 0.0200347
## T 7-T 3 -12.000000 -58.085796 34.085796 0.9877062
## T 8-T 3 58.000000 11.914204 104.085796 0.0086074
## T 9-T 3 -10.000000 -56.085796 36.085796 0.9962223
## T 5-T 4 -18.333333 -64.419129 27.752463 0.8763516
## T 6-T 4 -43.666667 -89.752463 2.419129 0.0705323
## T 7-T 4 -3.333333 -49.419129 42.752463 0.9999989
## T 8-T 4 66.666667 20.580871 112.752463 0.0023716
## T 9-T 4 -1.333333 -47.419129 44.752463 1.0000000
## T 6-T 5 -25.333333 -71.419129 20.752463 0.5900630
## T 7-T 5 15.000000 -31.085796 61.085796 0.9546944
## T 8-T 5 85.000000 38.914204 131.085796 0.0001740
## T 9-T 5 17.000000 -29.085796 63.085796 0.9134401
## T 7-T 6 40.333333 -5.752463 86.419129 0.1116698
## T 8-T 6 110.333333 64.247537 156.419129 0.0000069
## T 9-T 6 42.333333 -3.752463 88.419129 0.0849582
## T 8-T 7 70.000000 23.914204 116.085796 0.0014541
## T 9-T 7 2.000000 -44.085796 48.085796 1.0000000
## T 9-T 8 -68.000000 -114.085796 -21.914204 0.0019490
##
## $bloco
## diff lwr upr p adj
## B 2-B 1 0.4444444 -18.85487 19.74376 0.9980554
## B 3-B 1 -2.1111111 -21.41043 17.18820 0.9571497
## B 3-B 2 -2.5555556 -21.85487 16.74376 0.9379209plot(tukey)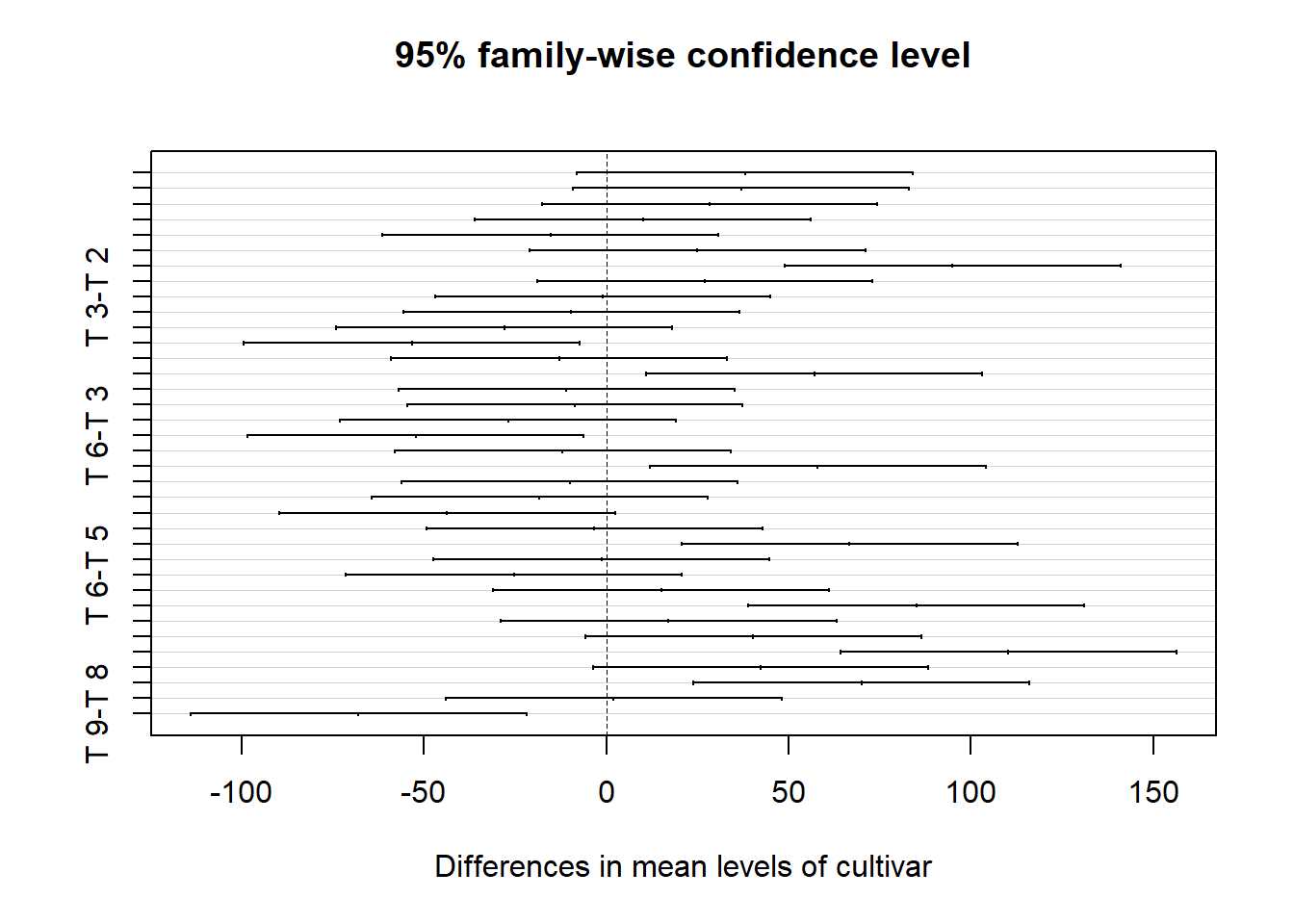
14.10.3 Teste de Comparação Múltipla de Tukey (Utilizando o HSD.test do Agricolae)
library(agricolae)
tukey=HSD.test(modelo,"cultivar")
plot(tukey)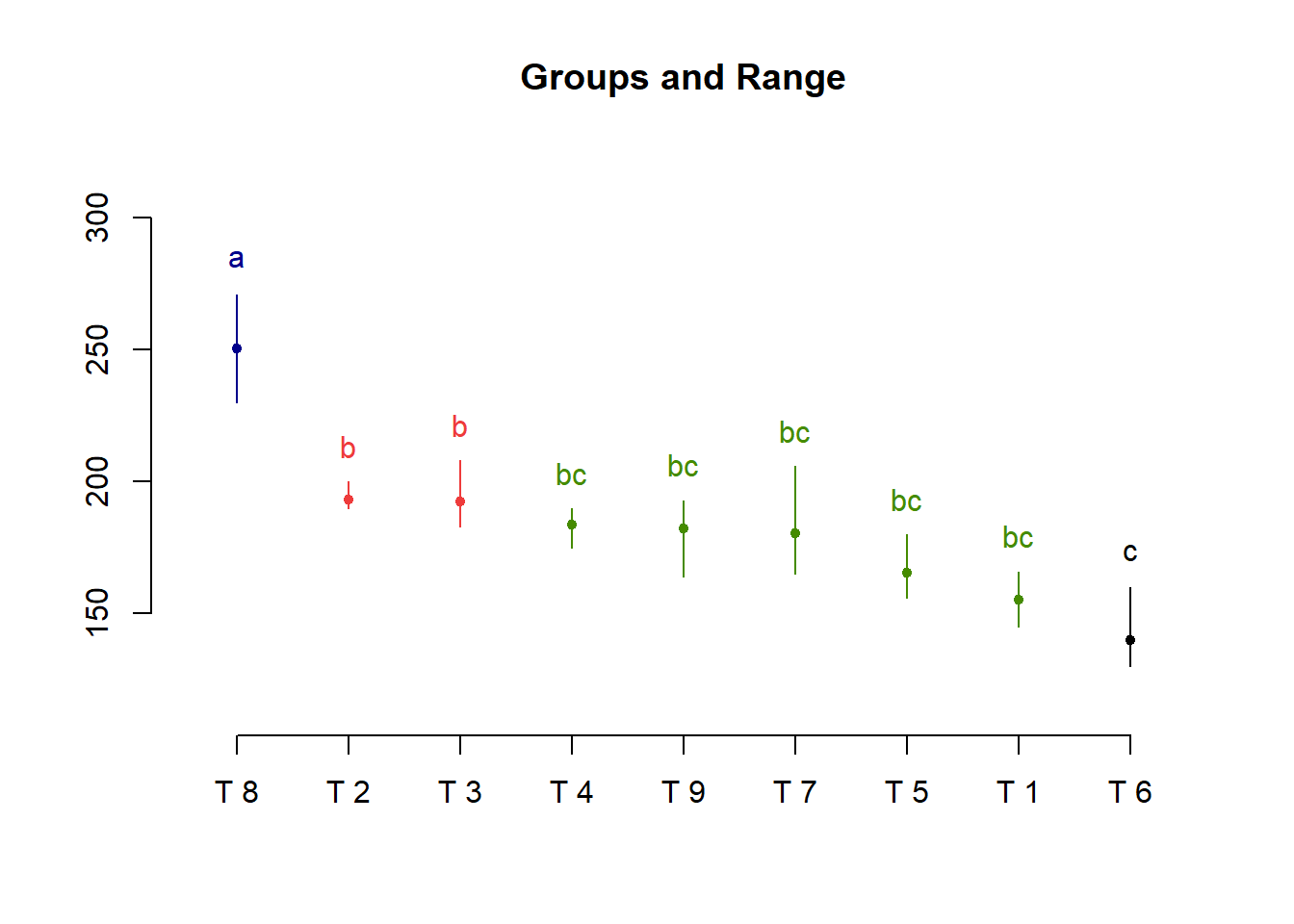
14.10.4 Teste de Comparação Múltipla de Tukey (Utilizando o ea1() do pacote easyanova)
library(easyanova)
tukey=ea1(data.frame(cultivar,bloco,resposta), design = 2)cbind(tukey$`Adjusted means`[1],tukey$`Adjusted means`[2],tukey$`Adjusted means`[4])## treatment adjusted.mean tukey
## 1 T 8 250.3333 a
## 2 T 2 193.3333 b
## 3 T 3 192.3333 b
## 4 T 4 183.6667 bc
## 5 T 9 182.3333 bc
## 6 T 7 180.3333 bc
## 7 T 5 165.3333 bc
## 8 T 1 155.3333 bc
## 9 T 6 140.0000 c14.10.4.1 Teste de Comparação Múltipla de Tukey (Utilizando o dbc do pacote ExpDes.pt)
library(ExpDes.pt)
dbc(cultivar,bloco,resposta)## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr>Fc
## Tratamento 8 22981.3 2872.67 11.4114 0.00003
## Bloco 2 33.6 16.78 0.0666 0.93578
## Residuo 16 4027.8 251.74
## Total 26 27042.7
## ------------------------------------------------------------------------
## CV = 8.69 %
##
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos
## valor-p: 0.187264
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
##
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia
## valor-p: 0.7817409
## De acordo com o teste de oneillmathews a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
##
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a T 8 250.3333
## b T 2 193.3333
## b T 3 192.3333
## bc T 4 183.6667
## bc T 9 182.3333
## bc T 7 180.3333
## bc T 5 165.3333
## bc T 1 155.3333
## c T 6 140
## ------------------------------------------------------------------------14.11 Exemplo 2

Um experimento foi realizado com o intuito de avaliar a produtividade de 15 cultivares comerciais de soja no munícipio de Londrina-PR. O experimento foi instalado em Delineamento em blocos casualizados com 3 repetições por tratamento.
Fonte da foto: Agricultura
14.11.1 Conjunto de dados
PRO=c(2444.44,2870.37,2314.81,2629.63,2444.44,2592.59,2962.96,3037.04,3037.04,2592.59,2296.30,2444.44,2370.37,3481.48,2555.56,1981.48,2611.11,1925.93,1870.37,2518.52,2370.37,2462.96,2351.85,2000.00,2703.70,2685.19,2166.67,2129.63,2222.22,1814.81,2537.04,2351.85,2333.33,3370.37,2462.96,3129.63,2666.67,2796.30,2055.56,2333.33,2240.74,2092.59,2703.70,2129.63,2740.74)
Cultivares=rep(c(paste("T",1:15)),e=3)
Bloco=rep(c(paste("B",1:3)),15)
Tratamento = as.factor(Cultivares)
bloco=as.factor(Bloco)
dados = data.frame(Tratamento, TRAT=Tratamento, bloco,resp=PRO)
dados = dados[order(dados$Tratamento), ]
X = 'Cultivares de soja'
(Y = expression(Produtividade (Kg.ha^-1)))## expression(Produtividade(Kg.ha^-1))alfa="0,05"14.12 Estatística descritiva
Média = with(dados, mean(resp))
Variância = with(dados, var(resp))
Desvio = with(dados, sd(resp))
CV = Desvio / Média * 100
desc = cbind(Média, Variância, Desvio, CV)
rownames(desc) = 'Produvidade (Kg/ha)'
kable(round(desc,2), align="l")| Média | Variância | Desvio | CV | |
|---|---|---|---|---|
| Produvidade (Kg/ha) | 2485.18 | 141049.6 | 375.57 | 15.11 |
14.12.1 Por Cultivar
Médias = with(dados, tapply(resp, Tratamento, mean))
Variâncias = with(dados, tapply(resp, Tratamento, var))
Desvios = with(dados, tapply(resp, Tratamento, sd))
CV = Desvios / Médias * 100
Desc = cbind(Médias, Variâncias, Desvios, CV)
kable(round(Desc,2),align="l")| Médias | Variâncias | Desvios | CV | |
|---|---|---|---|---|
| T 1 | 2543.21 | 84477.87 | 290.65 | 11.43 |
| T 10 | 2055.55 | 45611.24 | 213.57 | 10.39 |
| T 11 | 2407.41 | 12689.35 | 112.65 | 4.68 |
| T 12 | 2987.65 | 220966.26 | 470.07 | 15.73 |
| T 13 | 2506.18 | 156492.52 | 395.59 | 15.78 |
| T 14 | 2222.22 | 14746.18 | 121.43 | 5.46 |
| T 15 | 2524.69 | 117397.29 | 342.63 | 13.57 |
| T 2 | 2555.55 | 9602.62 | 97.99 | 3.83 |
| T 3 | 3012.35 | 1829.28 | 42.77 | 1.42 |
| T 4 | 2444.44 | 21946.94 | 148.15 | 6.06 |
| T 5 | 2802.47 | 354364.77 | 595.29 | 21.24 |
| T 6 | 2172.84 | 144831.90 | 380.57 | 17.51 |
| T 7 | 2253.09 | 115341.14 | 339.62 | 15.07 |
| T 8 | 2271.60 | 58412.64 | 241.69 | 10.64 |
| T 9 | 2518.52 | 92934.47 | 304.85 | 12.10 |
As Médias e as Variâncias estão apresentadas na Tabela . Nota-se uma variação nos valores médios, sendo a menor Média igual a \(2055.55\) e a maior Média de \(3012.35\). Já em relação às Variâncias, o menor valor é de \(1829.28\) e a maior variablidade de \(3.5436477\times 10^{5}\).
14.13 Gráfico de Caixas
par(bty='l', mai=c(1, 1, .2, .2))
par(cex=0.7)
caixas=with(dados, car::Boxplot(resp ~ dados$TRAT, vertical=T,las=1, col='Lightyellow',
xlab=X, ylab=Y))
mediab=tapply(dados$resp, dados$ TRAT, mean)
points(mediab, pch='+', cex=1.5, col='red')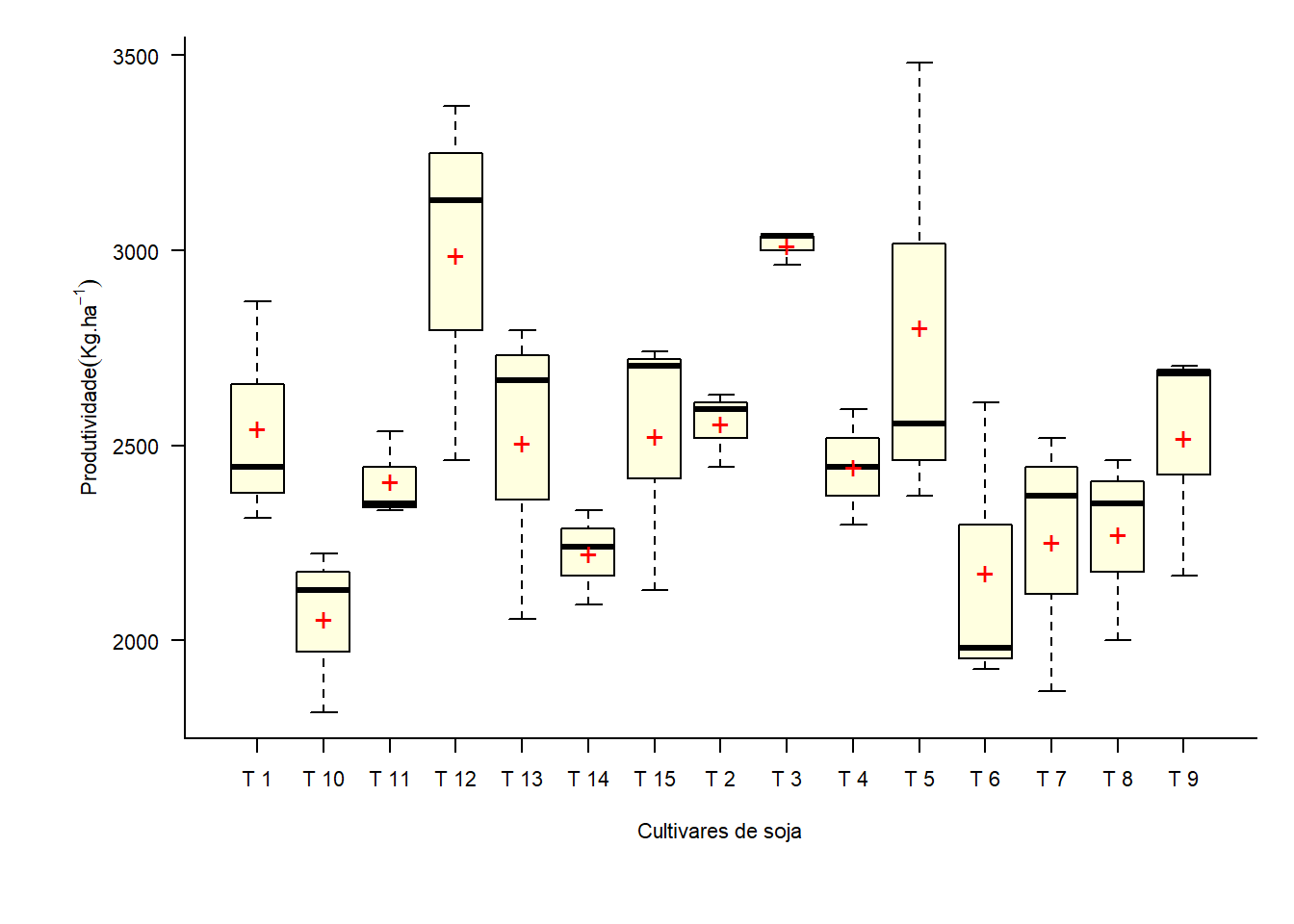
Figure 14.1: Gráfico de caixas
names(Desvios)[which.min(Desvios)]Não observa-se outliers. Há maior variabilidade em T 5 e menor em T 3, com 595.285 e 42.77, respectivamente. Há evidências de diferença entre as Médias dos tratamentos.
14.14 Análise de Variância
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 = \mu_3 = \cdots = \mu_{15} \\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
mod = with(dados, aov(resp ~ Tratamento+bloco))
av=anova(mod)
kable(av, align = "l")| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| Tratamento | 14 | 3302891.5 | 235920.82 | 2.545837 | 0.0171400 |
| bloco | 2 | 308550.2 | 154275.11 | 1.664793 | 0.2074184 |
| Residuals | 28 | 2594738.7 | 92669.24 |
Como p-valor calculado (p=\(0.01714\)) é menor que o nível de significância adotado (\(p=0,05\)), rejeita-se \(H0\). Logo, ao menos dois tratamentos se diferem entre si
14.15 Pressuposições
14.15.1 Normalidade dos erros
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{Os erros seguem distribuição normal}\\[.2cm] H_1: & \mbox{Os erros não seguem distribuição normal}. \end{array} \right. \end{eqnarray*}\]
(norm=shapiro.test(mod$res))##
## Shapiro-Wilk normality test
##
## data: mod$res
## W = 0.97989, p-value = 0.6151Como p-valor calculado (p=\(0.6151\)) é maior que o nível de significância adotado (\(\alpha=0,05\)), não rejeita-se \(H_O\). Logo, os erros seguem distribuição normal.
hnp::hnp(mod, las=1, xlab="Quantis teóricos", pch=16)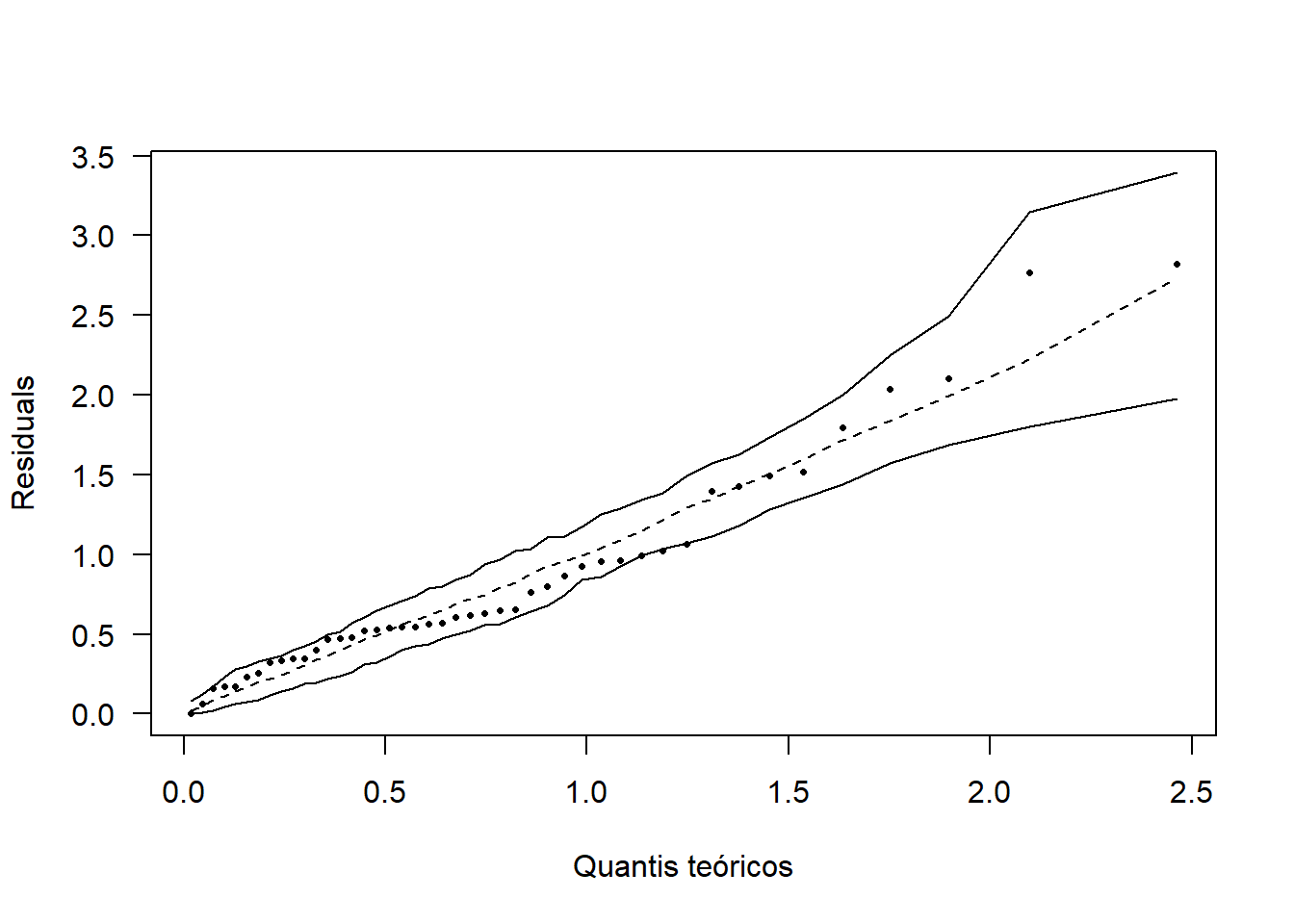
Figure 14.2: Gráfico QQplot
14.15.2 Homogeneidade de Variâncias
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{ As Variâncias são homogêneas}\\[.2cm] H_1: & \mbox{ As Variâncias não são homogêneas}. \end{array} \right. \end{eqnarray*}\]
(homog=with(dados, bartlett.test(mod$res ~ Tratamento)))##
## Bartlett test of homogeneity of variances
##
## data: mod$res by Tratamento
## Bartlett's K-squared = 15.293, df = 14, p-value = 0.3584Como p-valor calculado (p=\(0.3584\)) é maior que o nível de significância adotado (\(p=0,05\)), não rejeita-se \(H_0\). Logo, as Variâncias são homogêneas.
14.15.3 Independência dos erros
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: \mbox{Os erros são independentes}\\[.2cm] H_1: \mbox{Os erros não são independentes}. \end{array} \right. \end{eqnarray*}\]
(ind=lmtest::dwtest(mod))##
## Durbin-Watson test
##
## data: mod
## DW = 2.9611, p-value = 0.9272
## alternative hypothesis: true autocorrelation is greater than 0Como p-valor calculado (p=\(0.9272\)) é maior que o nível de significância adotado (\(p=0,05\)), não rejeita-se \(H_0\). Logo, os erros são independentes. A Figura apresenta os resíduos brutos. Percebe-se que os resíduos estão distribuídos de forma totalmente aleatória, evidenciando a sua independência.
plot(mod$res, las=1, pch=19, col='red', ylab='Resíduos brutos')
abline(h=0)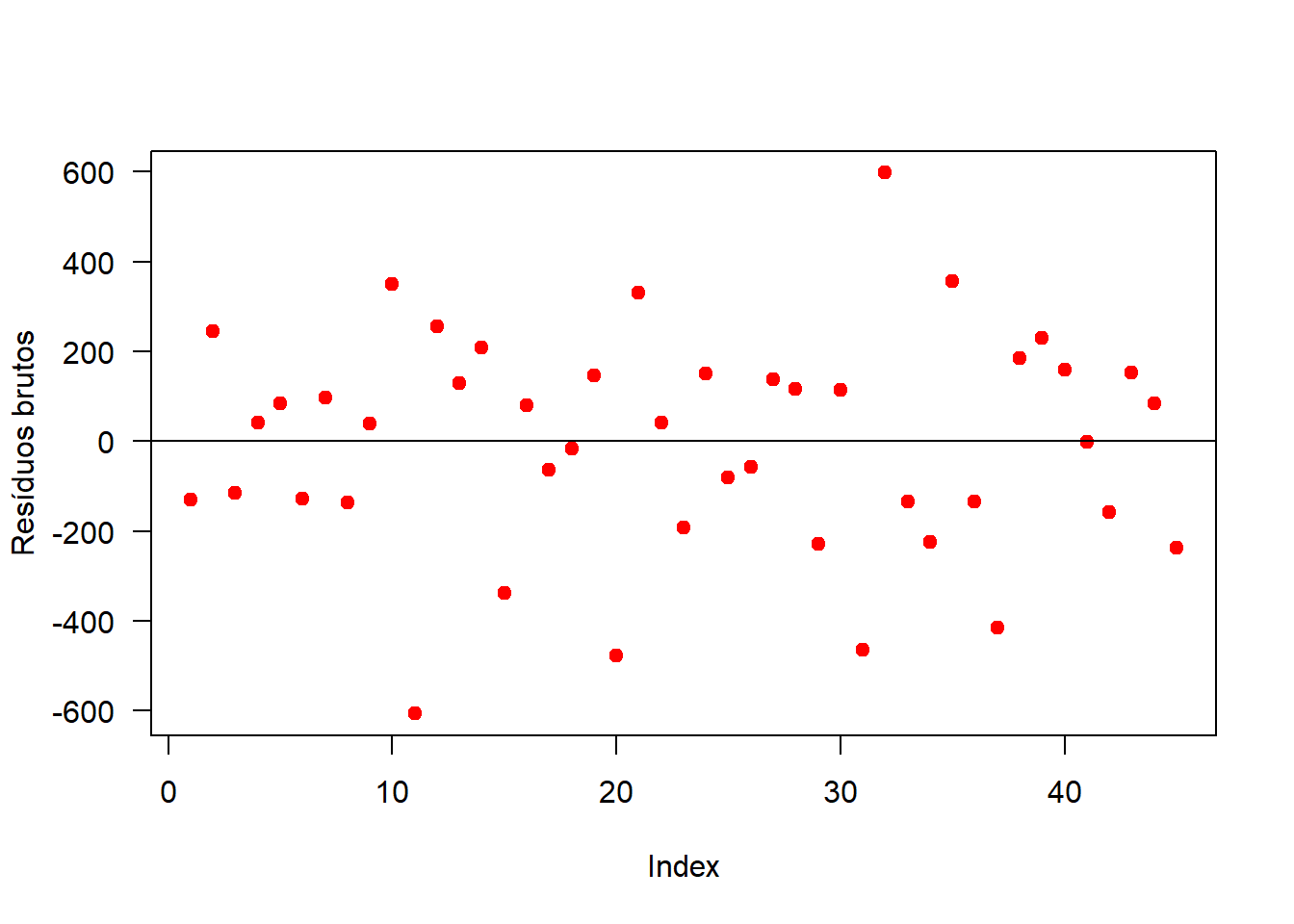
Figure 14.3: Gráfico de resíduos brutos
14.16 Teste de comparações
mod.1 = easyanova::ea1(dados[,c(1,3,4)], design=2, plot=2)tabela=cbind(mod.1$`Adjusted means`[1],
mod.1$`Adjusted means`[2],
mod.1$`Adjusted means`[8])
names(tabela)[1:3]=c("Cultivar","Média","")
kable(tabela, align = 'l', booktabs=T, caption="Teste de comparação de Scott-Knott", format="pandoc", format.args = list(big.mark="."))| Cultivar | Média | |
|---|---|---|
| T 3 | 3.012.347 | a |
| T 12 | 2.987.653 | a |
| T 5 | 2.802.470 | a |
| T 2 | 2.555.553 | b |
| T 1 | 2.543.207 | b |
| T 15 | 2.524.690 | b |
| T 9 | 2.518.520 | b |
| T 13 | 2.506.177 | b |
| T 4 | 2.444.443 | b |
| T 11 | 2.407.407 | b |
| T 8 | 2.271.603 | b |
| T 7 | 2.253.087 | b |
| T 14 | 2.222.220 | b |
| T 6 | 2.172.840 | b |
| T 10 | 2.055.553 | b |
library(ExpDes.pt)
with(dados,dbc(Tratamento, bloco,resp, mcomp="tukey"))## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr>Fc
## Tratamento 14 3302891 235921 2.5458 0.01714
## Bloco 2 308550 154275 1.6648 0.20742
## Residuo 28 2594739 92669
## Total 44 6206180
## ------------------------------------------------------------------------
## CV = 12.25 %
##
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos
## valor-p: 0.6150834
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
##
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia
## valor-p: 0.1187836
## De acordo com o teste de oneillmathews a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
##
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a T 3 3012.347
## a T 12 2987.653
## ab T 5 2802.47
## ab T 2 2555.553
## ab T 1 2543.207
## ab T 15 2524.69
## ab T 9 2518.52
## ab T 13 2506.177
## ab T 4 2444.443
## ab T 11 2407.407
## ab T 8 2271.603
## ab T 7 2253.087
## ab T 14 2222.22
## ab T 6 2172.84
## b T 10 2055.553
## ------------------------------------------------------------------------