13 Transformação de dados

---

• O modelo de Análise de Variância pressupõe que exista homocedasticidade, ou seja, que os tratamentos apresentem a mesma variabilidade;
• Algumas vezes este pressuposto pode não ser atendido e assim, para corrigir este problema existe uma saída por vezes bastante simples que é a transformação de dados;
• Esta técnica consiste na utilização de um artifício matemático para tornar o modelo de ANOVA válido.

---

13.1 Heterogeneidade Irregular

---

• Ocorre quando alguns tratamentos apresentam maior variabilidade do que outros, contudo, não existe uma associação entre média e variância;

• Neste caso, não há uma transformação matemática que elimine esta variabilidade.

Solução:

• Modelos Lineares Generalizados;

• Análise não paramétrica.

---

13.2 Heterogeneidade Regular

---

• Acontece quando existe alguma associação entre as médias dos tratamentos e a variância;
• A heterocedasticidade regular está associada é falta de normalidade do erros;

Solução:

• Transformação dos dados;

• Modelos Lineares Generalizados;

• Análise não paramétrica.

---

13.3 Princípio de transformação

---

Seja \(E(Y) = \mu\) a média de Y e suponha que o desvio padrão de Y é proporcional a potência da média de Y tal que:

\(\sigma Y \alpha \mu^\alpha.\)

O objetivo é encontrar uma transformação de \(Y\) que gere uma variância constante.

Suponha que a transformação é uma potência dos dados originais, isto é:

\(Y^*=Y^\lambda\)

Assim, pode ser mostrado que:

\(\sigma Y^* \alpha \mu^{\lambda+ \alpha-1}.\)

Caso \(\lambda = 1-\alpha\), então a variância dos dados transformados \(Y^*\) é constante, mostrando que não é necessário transformação.

Algumas das transformações mais comuns são:

\(\lambda\)	Transformação
1	Nenhuma
0,5	\(\sqrt{y}\)
0	log(y)
-0,5	\(\frac{1}{\sqrt{y}}\)
-1	\(\frac{1}{y}\)

---

13.4 Seleção Empírica de \(\alpha\)

---

Em muitas situações de delineamentos experimentais em que há repetições, pode-se estimar empiricamente \(\alpha\) a partir dos dados.

Dado que na i-ésima combinação de tratamentos

\(\sigma Y \alpha \mu^{\alpha}_i =\theta \mu^{\alpha}_i\)

em que \(\theta\) é uma constante de proporcionalidade, pode-se aplicar logaritmos para obter:

\(log (\sigma_{Y_i}) = log( \theta) + \alpha log( \mu_{i})\)

Portanto, um gráfico de \(log(\sigma_{Y_i})\) versus \(log(\mu_i)\) seria uma linha reta com uma inclinação \(\alpha\).

Como não se conhece \(\sigma_{Y_i}\) e \(\mu_i\) , utilizam-se as estimativas \(s_i\) e a média \(\hat{Y}_i\), respectivamente;

O parâmetro de inclinação da equação linear ajustada é uma estimativa de \(\alpha\).

---

13.5 Transf. de Box & Cox

---

Box & Cox (1964) mostraram como o parâmetro de transformação \(\lambda\) em \(Y^* = Y^\lambda\) pode ser estimado simultaneamente com outros parâmetros do modelo (média geral e efeitos de tratamentos) usando o método de máxima verossimilhança. O procedimento consiste em realizar, para vários valores de \(\lambda\), uma análise de variância padrão sobre:

\[Y_i(\lambda) = \left\{ \begin{array}{ll} \ln(X_i),~~~~~~\textrm{se $\lambda = 0$,} \\ \\ \dfrac{X_i^{\lambda} - 1}{\lambda},~~~~\textrm{se $\lambda \neq 0$,}\end{array} \right.\]

A estimativa de máxima verossimilhança de \(\lambda\) é o valor para o qual a soma de quadrado do resíduo, SQRes(\(\lambda\)), é mínima.

Este valor de \(\lambda\) é encontrado através do gráfico de SQRes(\(\lambda\)) versus \(\lambda\), sendo que \(\lambda\) é o valor que minimiza a SQRes(\(\lambda\)).

Ou, ainda, o valor de \(\lambda\) que maximiza a função de logverossimilhança.

Um intervalo de confiança \(100(1-\alpha)\)% para \(\lambda\) pode ser encontrado calculando-se:

\(IC(\lambda) = SQRes(\lambda)(1 \pm \frac{t2^2/2=2;v }{v})\)

em que \(v\) é o número de graus de liberdade.

Se o intervalo de confiança incluir o valor \(\lambda = 1\), isto quer dizer que não é necessário transformar os dados.

---

13.6 Exemplo 1

---

Vamos considerar os dados adaptados de ZAMBÃO; SAMPAIO; BARBIN, 1982 (Livro Planejamento e Análise Estatística de Experimentos Agronômicos - Décio Barbin) como exemplo, em que o pesquisador pretende comparar quatro cultivares de pêssego quanto ao enraizamento de estacas. Foi utilizado cinco repetições por tratamento e o delineamento experimental foi inteiramente casualizado.

Fonte da foto: Rosa, G.G., 2014 (Pelotas)

Tratamentos	R1	R2	R3	R4	R5	TOTAL
A	02	02	01	01	00	06
B	01	00	00	01	01	03
C	12	10	14	17	11	64
D	07	09	15	08	10	49

13.7 Conjunto de dados

resposta=c(02,02,01,01,00,01,00,00,01,01,12,10,14,17,11,07,09,15,08,10)
cultivar=rep(LETTERS[1:4],e=5)
cultivar=as.factor(cultivar)

13.8 Gráficos exploratórios

13.8.1 Gráfico de caixas

car::Boxplot(resposta~cultivar)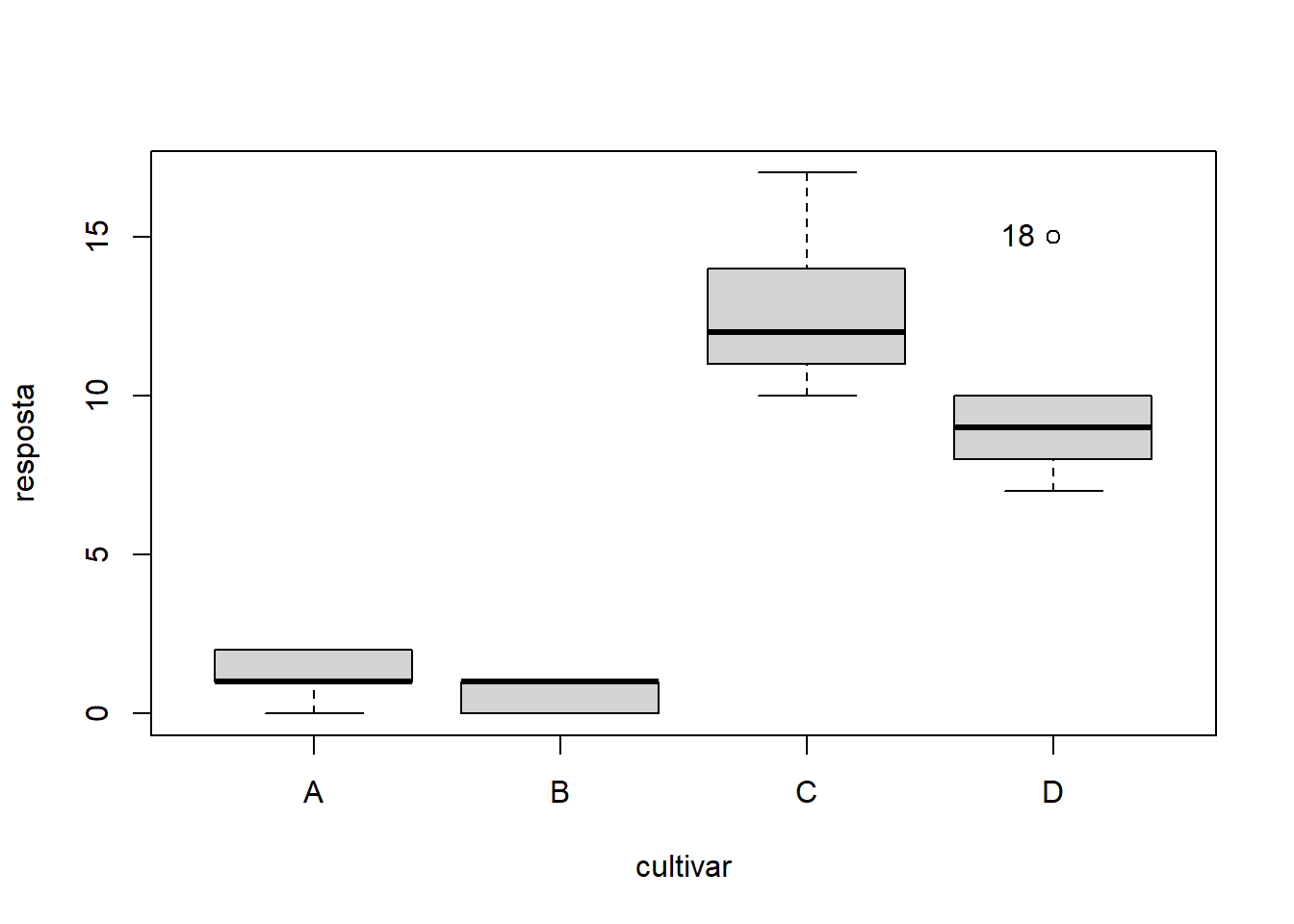

## [1] "18"

13.8.2 Histograma

hist(resposta)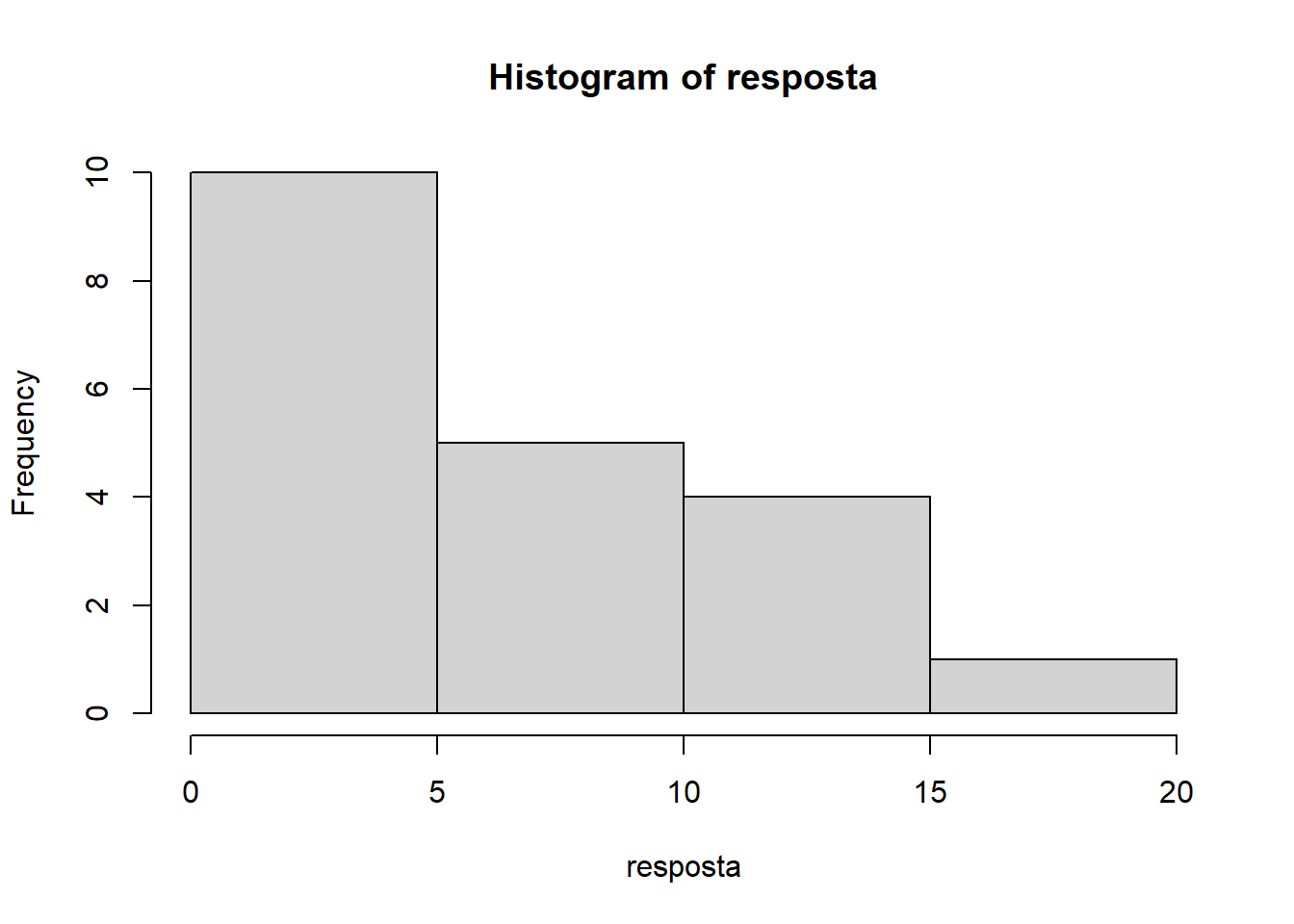

13.9 Análise de variância

modelo=aov(resposta~cultivar)
anova(modelo) # Conferir GL

## Analysis of Variance Table
## 
## Response: resposta
##           Df Sum Sq Mean Sq F value    Pr(>F)    
## cultivar   3  564.2  188.07  40.884 9.945e-08 ***
## Residuals 16   73.6    4.60                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

13.10 Pressuposições

13.10.1 Normalidade dos erros

shapiro.test(modelo$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  modelo$residuals
## W = 0.88533, p-value = 0.02209

Os erros não seguem distribuição normal

13.10.2 Homogeneidade das variâncias

bartlett.test(modelo$residuals~cultivar)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  modelo$residuals by cultivar
## Bartlett's K-squared = 12.141, df = 3, p-value = 0.006914

As variâncias não são homogêneas

13.10.3 Independência dos erros

lmtest::dwtest(modelo)

## 
##  Durbin-Watson test
## 
## data:  modelo
## DW = 2.269, p-value = 0.4631
## alternative hypothesis: true autocorrelation is greater than 0

Os erros são independentes.

13.10.4 Gráfico de resíduos padronizados

a=anova(modelo)
plot(modelo$residuals/sqrt(a$`Mean Sq`[2]), ylab="Resíduos Padronizados")
abline(h=0)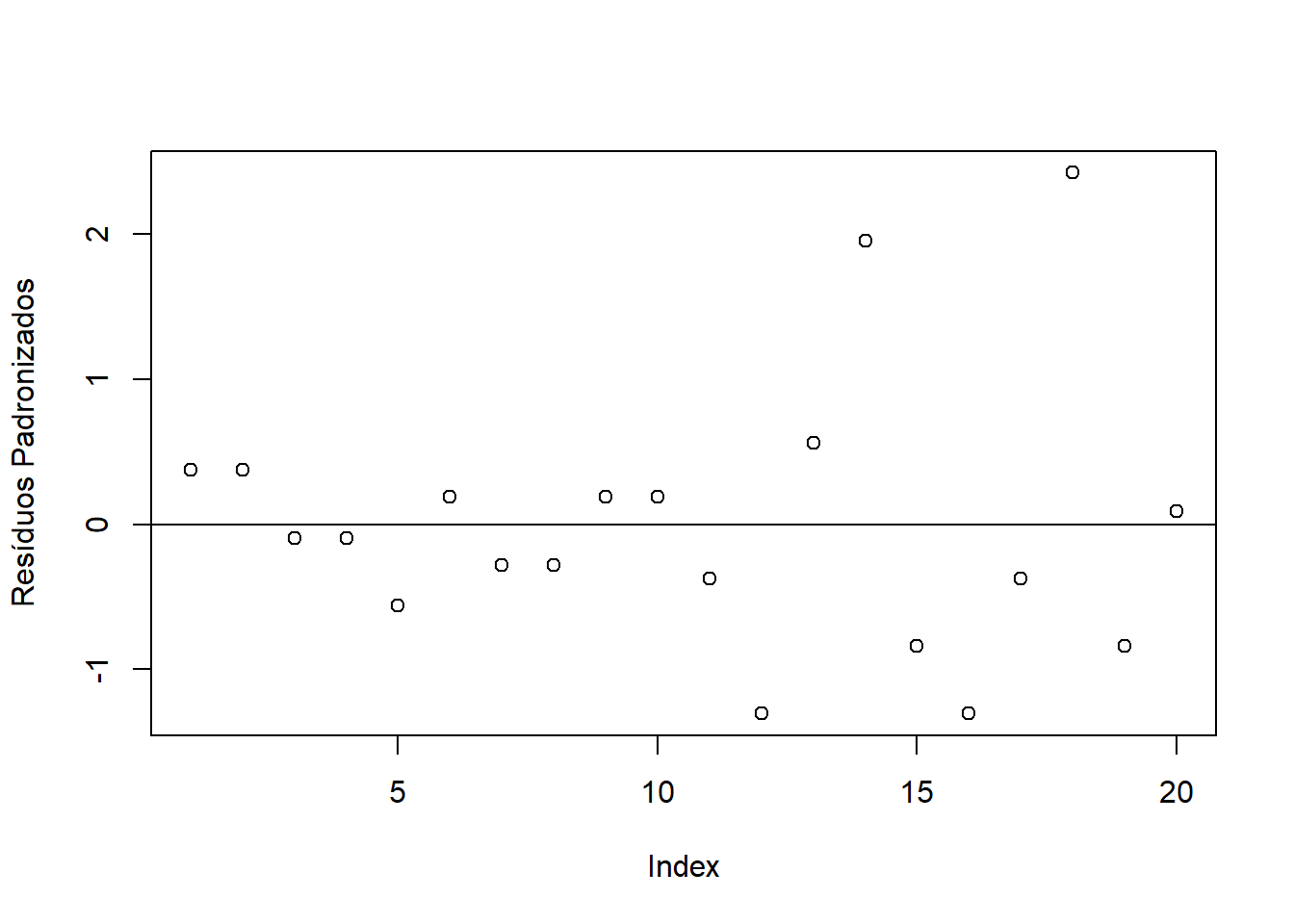

As pressuposições de normalidade dos erros e homogeneidade das variâncias não foram atendidas. Dessa forma, vamos transformar os dados e conferir novamente as pressuposições!

13.11 Transformação de dados

13.11.1 Usando a package MASS

13.11.2 Usando o comando boxcox e conferindo visualmente um valor aproximado de \(\lambda\)

# MASS::boxcox(modelo) ## o comando boxcox do pacote MASS não aceita quando ocorre observações 0
# vamos somar uma constante com valor "baixo"
MASS::boxcox(aov(resposta+0.000001~cultivar))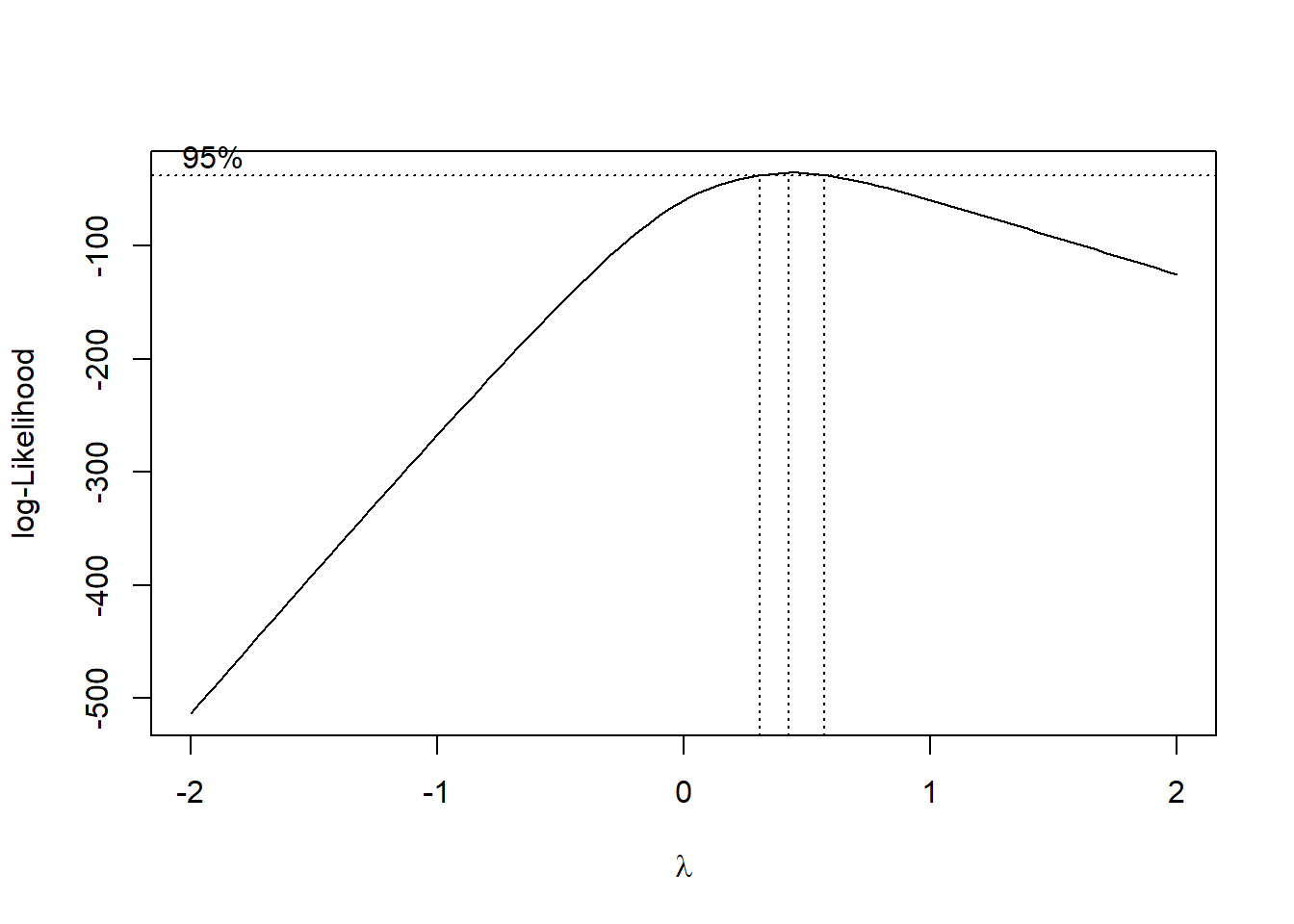

13.11.3 Descobrindo o valor exato de \(\lambda\)

bc=MASS::boxcox(aov(resposta+0.000001~cultivar))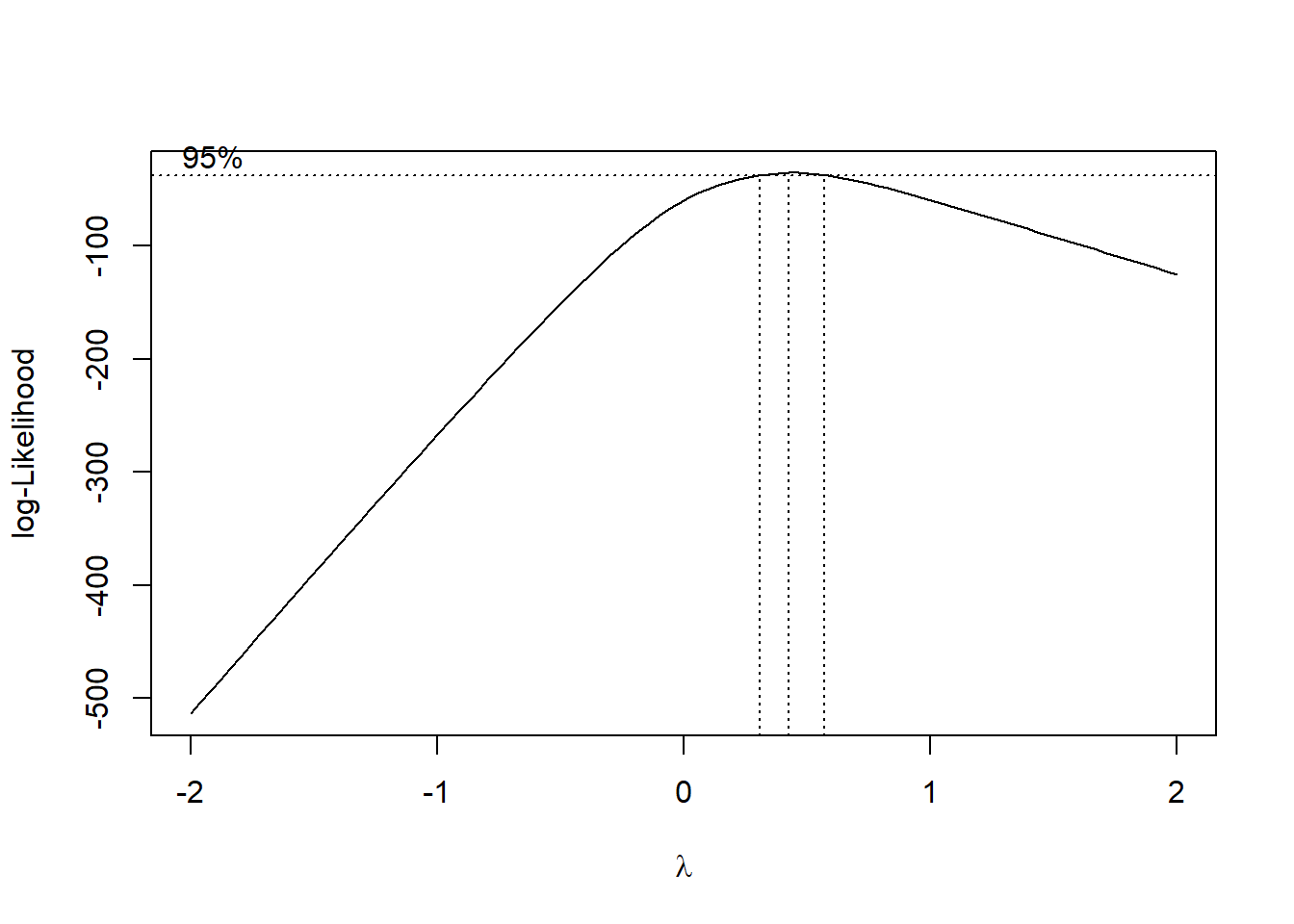

bc$x[which.max(bc$y)]

## [1] 0.4242424

A aproximação de \(\lambda\) é 0,5 (sqrt(Y))

13.12 Dados transformados

13.12.1 Modelo transformado

modelo=aov(resposta^0.5~cultivar)
#ou
modelo=aov(sqrt(resposta)~cultivar)

13.12.2 Normalidade dos erros

shapiro.test(modelo$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  modelo$residuals
## W = 0.96828, p-value = 0.7182

Os erros seguem distribuição normal

13.12.3 Homogeneidade das variâncias

bartlett.test(modelo$residuals~cultivar)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  modelo$residuals by cultivar
## Bartlett's K-squared = 0.71659, df = 3, p-value = 0.8693

As variâncias são homogêneas

13.12.4 Independência dos erros

lmtest::dwtest(modelo)

## 
##  Durbin-Watson test
## 
## data:  modelo
## DW = 2.1575, p-value = 0.3596
## alternative hypothesis: true autocorrelation is greater than 0

Os erros são independentes.

13.12.5 Gráfico de resíduos padronizados

a=anova(modelo)
plot(modelo$residuals/sqrt(a$`Mean Sq`[2]), ylab="Resíduos Padronizados")
abline(h=0)

13.13 Comparação múltipla

13.13.1 Teste de Comparação Múltipla de Tukey (Utilizando o multcomp)

library(multcomp)
mcomp=glht(modelo, mcp(cultivar="Tukey"))
plot(mcomp)

cld(mcomp)

##   A   B   C   D 
## "a" "a" "b" "b"

13.13.2 Teste de Comparação Múltipla de Tukey (Utilizando o TukeyHSD do R)

(tukey=TukeyHSD(modelo))

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = sqrt(resposta) ~ cultivar)
## 
## $cultivar
##           diff       lwr       upr     p adj
## B-A -0.3656854 -1.271030 0.5396592 0.6619314
## C-A  2.5958680  1.690523 3.5012126 0.0000022
## D-A  2.1362025  1.230858 3.0415471 0.0000252
## C-B  2.9615534  2.056209 3.8668981 0.0000004
## D-B  2.5018879  1.596543 3.4072325 0.0000035
## D-C -0.4596655 -1.365010 0.4456791 0.4869422

plot(tukey)

13.13.3 Teste de Comparação Múltipla de Tukey (Utilizando o HSD.test do Agricolae)

library(agricolae)
tukey=HSD.test(modelo,"cultivar")
plot(tukey)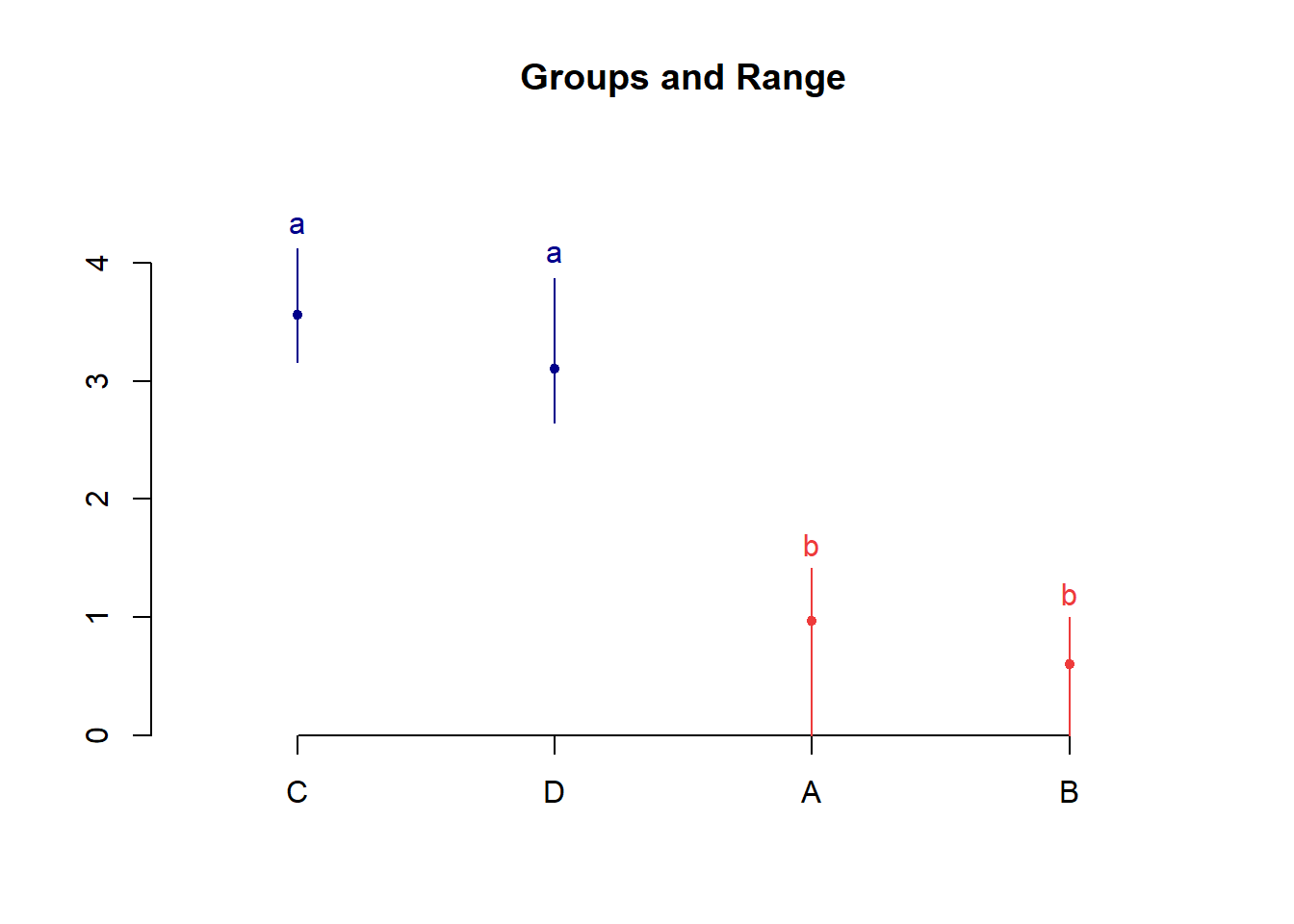

13.13.4 Teste de Comparação Múltipla de Tukey (Utilizando o ea1() do pacote easyanova)

library(easyanova)
tukey=ea1(data.frame(cultivar,resposta^0.5))

cbind(tukey$Means[1],tukey$Means[2],tukey$Means[4])

##   treatment   mean tukey
## 1         C 3.5616     a
## 2         D 3.1019     a
## 3         A 0.9657     b
## 4         B 0.6000     b

13.13.5 Teste de Comparação Múltipla de Tukey (Utilizando o dic do pacote ExpDes.pt)

library(ExpDes.pt)
dic(cultivar,resposta^0.5)

## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
##            GL     SQ      QM     Fc      Pr>Fc
## Tratamento  3 33.346 11.1155 44.402 5.5521e-08
## Residuo    16  4.005  0.2503                  
## Total      19 37.352                          
## ------------------------------------------------------------------------
## CV = 24.32 %
## 
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos ( Shapiro-Wilk ) 
## Valor-p:  0.7181511 
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia 
## valor-p:  0.8692942 
## De acordo com o teste de bartlett a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
## 
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a     C   3.561553 
## a     D   3.101888 
##  b    A   0.9656854 
##  b    B   0.6 
## ------------------------------------------------------------------------

---

13.14 Exemplo 2

---

13.14.1 Conjunto de dados

Um experimento foi conduzido com o intuito de avaliar a inoculação de Trichoderma sp. (T4), Azospirillum sp. (T3) e associação de ambos (T2) em relação a testemunha, quanto à altura de plantas de milho. O experimento foi conduzido em delineamento inteiramente casualizado com 8 repetições.

RESP=c(124,136,124,102,112,108,102,122,
       130,128,118,106,126,106,128,122,
       132,132,190,144,090,126,142,148,
       140,120,118,098,110,140,104,142)
TRAT=rep(c(paste("T",1:4)),e=8)
dados = data.frame(TRAT, RESP)

13.15 Estatística descritiva

Média = with(dados, mean(RESP))
Variância = with(dados, var(RESP))
Desvio = with(dados, sd(RESP))
CV = Desvio / Média * 100

desc = cbind(Média, Variância, Desvio, CV)
kable(round(desc,2), align="l")

Média	Variância	Desvio	CV
124.06	367.09	19.16	15.44

13.15.1 Por Cultivar

Médias = with(dados, tapply(RESP, TRAT, mean))
Variâncias = with(dados, tapply(RESP, TRAT, var))
Desvios = with(dados, tapply(RESP, TRAT, sd))
CV = Desvios / Médias * 100
Desc = cbind(Médias, Variâncias, Desvios, CV)
kable(round(Desc,2),align="l")

	Médias	Variâncias	Desvios	CV
T 1	116.25	147.93	12.16	10.46
T 2	120.50	94.57	9.72	8.07
T 3	138.00	768.00	27.71	20.08
T 4	121.50	301.43	17.36	14.29

13.16 Gráficos exploratórios

13.16.1 Gráfico de Caixas

par(bty='l', mai=c(1, 1, .2, .2))
par(cex=0.7)
caixas=with(dados, car::Boxplot(RESP ~ dados$TRAT, vertical=T,las=1, col='Lightyellow'))
mediab=tapply(RESP, TRAT, mean)
points(mediab, pch='+', cex=1.5, col='red')

13.17 Análise de Variância

\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 = \mu_3 = \cdots = \mu_{15} \\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]

mod = with(dados, aov(RESP ~ TRAT))
av=anova(mod)
kable(av, align = "l")

	Df	Sum Sq	Mean Sq	F value	Pr(>F)
TRAT	3	2196.375	732.1250	2.23221	0.1064722
Residuals	28	9183.500	327.9821

13.18 Pressuposições

13.18.1 Normalidade dos erros

\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{Os erros seguem distribuição normal}\\[.2cm] H_1: & \mbox{Os erros não seguem distribuição normal}. \end{array} \right. \end{eqnarray*}\]

(norm=shapiro.test(mod$res))

## 
##  Shapiro-Wilk normality test
## 
## data:  mod$res
## W = 0.94078, p-value = 0.07878

Como p-valor calculado (\(p=0,07878\)) é maior que o nível de significância adotado (\(p=0,05\)), não se rejeita \(H_0\). Logo, os erros seguem distribuição normal.

hnp::hnp(mod, las=1, xlab="Quantis teóricos", pch=16)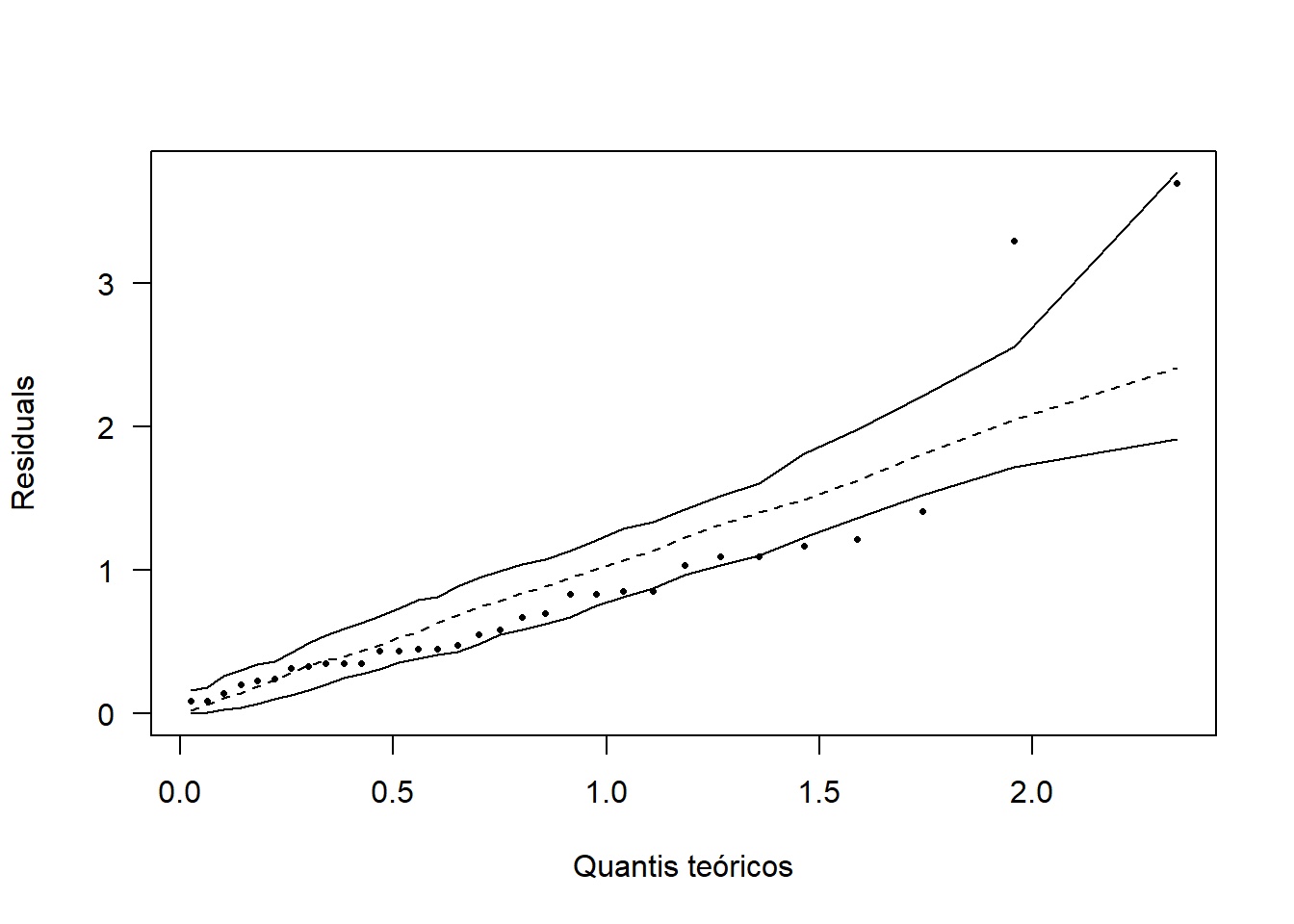

13.18.2 Homogeneidade de variâncias

\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{ As variâncias são homogêneas}\\[.2cm] H_1: & \mbox{ As variâncias não são homogêneas}. \end{array} \right. \end{eqnarray*}\]

(homog=with(dados, bartlett.test(mod$res ~ TRAT)))

## 
##  Bartlett test of homogeneity of variances
## 
## data:  mod$res by TRAT
## Bartlett's K-squared = 8.4132, df = 3, p-value = 0.0382

Como p-valor (\(p=0,0382\)) é menor que o nível de significância adotado (\(p=0,05\)). Rejeita-se \(H_0\), logo, as variâncias dos erros não são homogêneas.

13.19 Transformação de dados

library(MASS)
bc=boxcox(mod)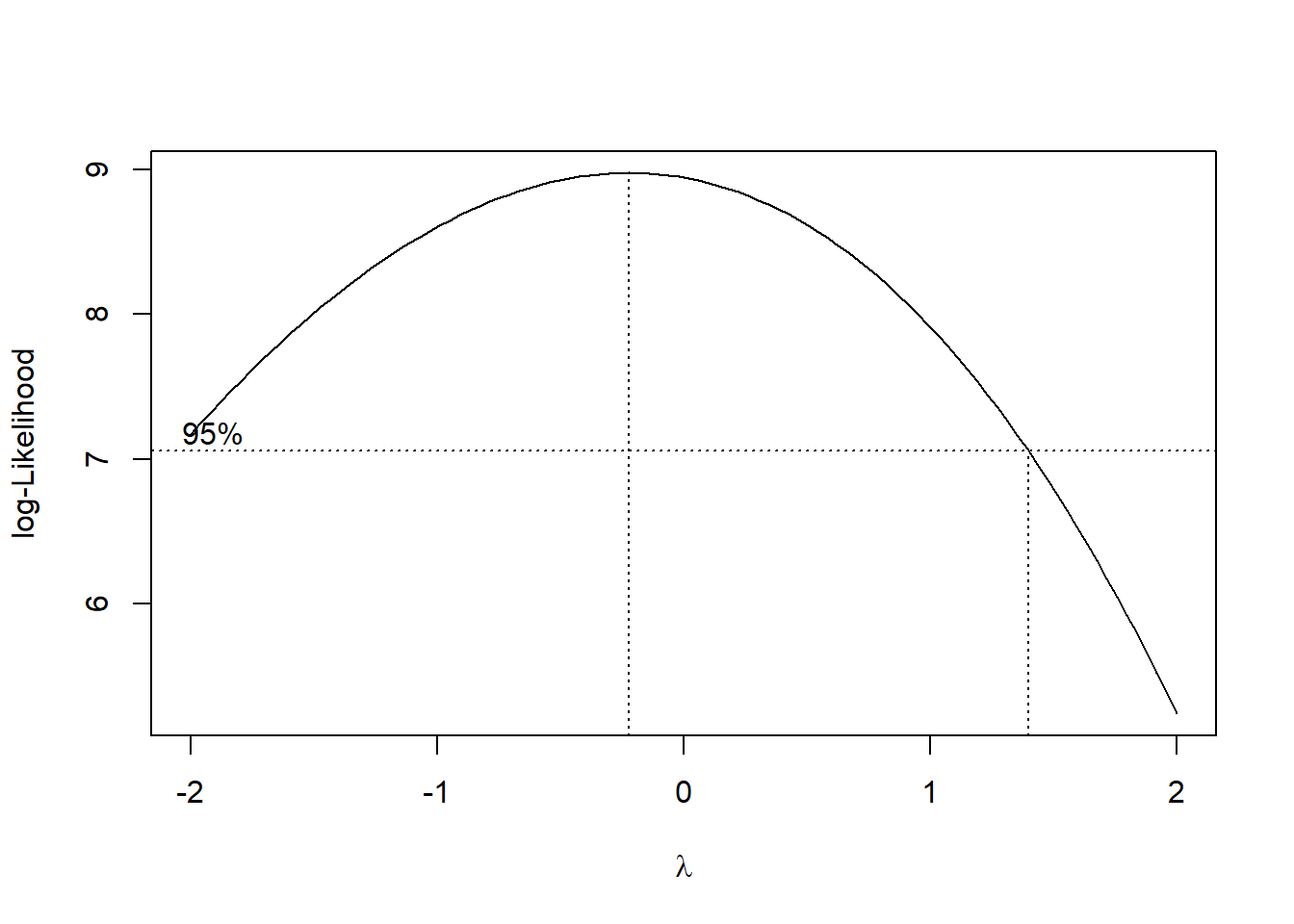

bc$x[which.max(bc$y)]

## [1] -0.2222222

O valor de \(\lambda\) para a Transformação Box-Cox é -0,22222. Nesse sentido, vamos usar a aproximação. Logo, iremos usar a Transformação Log

13.19.1 Transformação log

13.19.2 Modelo com dados transformados

Devemos testar novamente as pressuposições após a Transformação!!!

modelo=aov(log(RESP)~TRAT)
anova(modelo)

## Analysis of Variance Table
## 
## Response: log(RESP)
##           Df  Sum Sq  Mean Sq F value Pr(>F)
## TRAT       3 0.11275 0.037583  1.8407 0.1627
## Residuals 28 0.57170 0.020418

Como p-valor da análise de variância (\(p=0,1627\)) é maior que o nível de significância adotado, não se rejeita \(H_0\). Logo, não há evidências de diferença entre os tratamentos.

13.19.3 Normalidade dos erros

shapiro.test(modelo$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  modelo$residuals
## W = 0.95442, p-value = 0.1922

13.19.4 Homogeneidade das variâncias

bartlett.test(modelo$residuals~TRAT)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  modelo$residuals by TRAT
## Bartlett's K-squared = 6.2678, df = 3, p-value = 0.09928

13.19.5 Independências dos erros

lmtest::dwtest(modelo)

## 
##  Durbin-Watson test
## 
## data:  modelo
## DW = 1.9204, p-value = 0.216
## alternative hypothesis: true autocorrelation is greater than 0

13.19.6 Usando os pacotes easyanova e ExpDes.pt

dados=data.frame(TRAT,log(RESP))
easyanova::ea1(dados, design=1, plot=2)

## $`Analysis of variance`
##            df type I SS mean square F value    p>F
## treatments  3    0.1127      0.0376  1.8407 0.1627
## Residuals  28    0.5717      0.0204       -      -
## 
## $Means
##   treatment   mean standard.error tukey snk duncan  t scott_knott
## 1       T 3 4.9089         0.0505     a   a      a  a           a
## 2       T 4 4.7909         0.0505     a   a      a ab           a
## 3       T 2 4.7887         0.0505     a   a      a ab           a
## 4       T 1 4.7510         0.0505     a   a      a  b           a
## 
## $`Multiple comparison test`
##        pair contrast p(tukey) p(snk) p(duncan)   p(t)
## 1 T 3 - T 4   0.1180   0.3671 0.1097    0.1097 0.1097
## 2 T 3 - T 2   0.1202   0.3512 0.2293    0.1221 0.1035
## 3 T 3 - T 1   0.1579   0.1449 0.1449    0.0509 0.0354
## 4 T 4 - T 2   0.0022   1.0000 0.9756    0.9756 0.9756
## 5 T 4 - T 1   0.0399   0.9434 0.8429    0.6036 0.5808
## 6 T 2 - T 1   0.0377   0.9516 0.6017    0.6017 0.6017
## 
## $`Residual analysis`
## $`Residual analysis`$`residual analysis`
##                               values
## p.value Shapiro-Wilk test     0.1922
## p.value Bartlett test         0.0993
## coefficient of variation (%)  2.9700
## first value most discrepant  21.0000
## second value most discrepant 19.0000
## third value most discrepant  28.0000
## 
## $`Residual analysis`$residuals
##            1            2            3            4            5            6 
##  0.069304717  0.161678037  0.069304717 -0.126004035 -0.032477977 -0.068845621 
##            7            8            9           10           11           12 
## -0.126004035  0.053044196  0.078851858  0.063347671 -0.017997968 -0.125243499 
##           13           14           15           16           17           18 
##  0.047599314 -0.125243499  0.063347671  0.015338452 -0.026144593 -0.026144593 
##           19           20           21           22           23           24 
##  0.338077556  0.060866784 -0.409136845 -0.072664609  0.046880542  0.088265758 
##           25           26           27           28           29           30 
##  0.150751546 -0.003399134 -0.020206252 -0.205923398 -0.090410511  0.150751546 
##           31           32 
## -0.146499978  0.164936181 
## 
## $`Residual analysis`$`standardized residuals`
##           1           2           3           4           5           6 
##  0.51034208  1.19055541  0.51034208 -0.92786125 -0.23915946 -0.50696142 
##           7           8           9          10          11          12 
## -0.92786125  0.39060380  0.58064476  0.46647593 -0.13253240 -0.92226086 
##          13          14          15          16          17          18 
##  0.35050909 -0.92226086  0.46647593  0.11294841 -0.19252205 -0.19252205 
##          19          20          21          22          23          24 
##  2.48951602  0.44820731 -3.01277832 -0.53508346  0.34521623  0.64996630 
##          25          26          27          28          29          30 
##  1.11009554 -0.02503035 -0.14879364 -1.51636685 -0.66575971  1.11009554 
##          31          32 
## -1.07878809  1.21454754

library(ExpDes.pt)
with(dados,dic(TRAT,log(RESP), mcomp="tukey"))

## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
##            GL      SQ       QM     Fc  Pr>Fc
## Tratamento  3 0.11275 0.037583 1.8407 0.1627
## Residuo    28 0.57170 0.020418              
## Total      31 0.68444                       
## ------------------------------------------------------------------------
## CV = 2.97 %
## 
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos ( Shapiro-Wilk ) 
## Valor-p:  0.1921639 
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
## 
## ------------------------------------------------------------------------
## Teste de homogeneidade de variancia 
## valor-p:  0.09928479 
## De acordo com o teste de bartlett a 5% de significancia, as variancias podem ser consideradas homogeneas.
## ------------------------------------------------------------------------
## 
## De acordo com o teste F, as medias nao podem ser consideradas diferentes.
## ------------------------------------------------------------------------
##   Niveis   Medias
## 1    T 1 4.750977
## 2    T 2 4.788683
## 3    T 3 4.908947
## 4    T 4 4.790891
## ------------------------------------------------------------------------

---