15 Delineamento em Quadrado Latino

---

• Na sessão de delineamento em blocos ao acaso, observamos que o mesmo é usado para reduzir o erro residual de um experimento utilizando o princípio do controle local;
• No Delineamento em Quadrado Latino, além dos princípios da repetição e da casualização, o princípio do controle local é utilizado duas vezes para controlar o efeito de dois fatores;
• Para controlar esta variabilidade, é necessário dividir as unidades experimentais em blocos homogêneos de unidades experimentais em relação a cada fator controlado.
• O número de blocos para cada fator controlado deve ser igual ao número de tratamentos. Uma vez formados os blocos, distribui-se os tratamentos ao acaso com a restrição que cada tratamento seja designado uma única vez em cada um dos blocos dos dois fatores controlados.
• Os níveis de um fator controlado são identificados por linhas em uma tabela de dupla entrada e os níveis do outro fator controlado são identificados por colunas na tabela.
• A grande restrição dos ensaios em quadrados latinos é que para 2, 3 ou 4 tratamentos teremos apenas 0, 2 ou 6 g.l., respectivamente,para o resíduo.
• Por outro lado, com 9 ou mais tratamentos, o quadrado latino fica muito grande, trazendo dificuldades na instalação, pois, para 9 tratamentos, teremos 81 parcelas.
• Por isso, os quadrados latinos mais usados são os de 5 x 5, 6 x 6, 7 x 7 e 8 x 8.

---

15.1 Modelo matemático

---

\[\begin{eqnarray} y_{ji}=\mu+\tau_i+\alpha_j+\beta_k+\varepsilon_{ij} \end{eqnarray}\]

\(y_{ji}\): é o valor observado na i-ésima linha e k-ésima coluna para o j-ésimo tratamento;

\(\mu\): é a média geral (ou constante comum a todas as observações);

\(\tau_i\): é o efeito de tratamento, com \(i = 1, 2, . . . , I\);

\(\beta_j\): é o efeito da k-ésima coluna;

\(\alpha_j\): é efeito da j-ésima linha

\(\varepsilon_{ij}\): é o erro experimental, tal que \(\varepsilon_{ij}\)~N(0; \(\sigma^2\)).

O modelo é completamente aditivo, ou seja, não há interação entre linhas, colunas e tratamentos.

---

15.2 Hipóteses e Modelo

---

\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 =\mu_i\\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]

CV	G.L.	S.Q.	Q.M.	Fcalc	Ftab
Tratamentos	\(p - 1\)	\(SQ_{Trat}\)	\(\frac{SQ_{Trat}}{p-1}\)	\(\frac{QMTrat}{QMRes}\)	\(F(\alpha;GL_{Trat} ;GL_{Res})\)
Linhas	\(p - 1\)	\(SQ_{L}\)	\(\frac{SQ_{L}}{p-1}\)	\(\frac{QM_{L}}{QM_{Res}}\)	\(F(\alpha;GL_{L} ;GL_{Res})\)
Colunas	\(p - 1\)	\(SQ_{C}\)	\(\frac{SQ_{C}}{p-1}\)	\(\frac{QM_{C}}{QM_{Res}}\)	\(F(\alpha;GL_{C} ;GL_{Res})\)
resíduo	\((p-2)(p-1)\)	\(SQ_{Res}\)	\(\frac{SQRes}{(p-2)(p-1)}\)
Total	\(p^2-1\)	\(SQ_{Total}\)

---

15.2.1 Croqui de um experimento em DQL

---

Criando uma função para fazer um croqui

# Não alterar os comandos da função
library(agricolae)
library(gridExtra)
library(grid)
croqui=function(trat){
  r=length(trat)
  sort=design.lsd(trat,r,serie=0)
  sort$book[,4]=as.factor(matrix(sort$book[,4],r,,T))
  ncol=r
  gs <- lapply(sort$book[,4], function(ii)
    grobTree(rectGrob(gp=gpar(fill=ii, alpha=0.5)),textGrob(ii)))
  grid.arrange(grobs=gs, ncol=ncol)}

Vetor de tratamentos

trat=c("T1","T2","T3","T4")

Usando a função

croqui(trat)

---

15.3 Exemplo 1

---

Considere um experimento, cujo objetivo foi estudar o efeito da idade de castração no desenvolvimento e produção de suínos, avaliando-se o peso dos leitões. Quatro tratamentos foram estudados:

• A - castração aos 56 dias de idade;
• B - castração aos 7 dias de idade;
• C - castração aos 36 dias de idade;
• D - inteiros (não castrados);
• E - castração aos 21 dias de idade;

Foi utilizado o delineamento em quadrado latino buscando controlar a variação entre leitegadas (linhas) e a variação no peso inicial dos leitões (colunas), sendo a parcela experimental constituída de um leitão. Os ganhos de pesos, em kg, após o período experimental (28 semanas), estão apresentados no quadro abaixo:

Linhas	Coluna 1	Coluna 2	Coluna 3	Coluna 4	Coluna 5	Totais
Leitegada 1	93,0(A)	115,4(C)	116,9(E)	110,2(D)	110,4(B)	545,9
Leitegada 2	110,6(C)	96,5(E)	108,9(B)	97,6 (A)	112,0(D)	525,6
Leitegada 3	102,1(B)	108,6(D)	77,9(A)	102,0(E)	111,7(C)	502,3
Leitegada 4	115,4(D)	94,9(A)	114,0(C)	100,2(B)	118,5(E)	543,0
Leitegada 5	117,6(E)	114,1(B)	118,7(D)	108,8(C)	80,2(A)	539,4
Totais	538,7	529,5	536,4	518,8	532,8	2656,2

15.3.1 Conjunto de dados

RESP=c(93.0, 115.4, 116.9, 110.2, 110.4,110.6, 96.5, 108.9, 97.6, 112.0,102.1, 108.6, 77.9, 102.0, 111.7,115.4, 94.9, 114.0, 100.2, 118.5,117.6, 114.1, 118.7, 108.8, 80.2)
(TRAT=c("A","C","E","D","B","C","E","B","A","D","B","D","A","E","C","D","A","C","B","E","E","B","D","C","A"))

##  [1] "A" "C" "E" "D" "B" "C" "E" "B" "A" "D" "B" "D" "A" "E" "C" "D" "A" "C" "B"
## [20] "E" "E" "B" "D" "C" "A"

(linha=as.factor(rep(1:5,each=5)))

##  [1] 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5
## Levels: 1 2 3 4 5

(coluna=as.factor(rep(1:5,5)))

##  [1] 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5
## Levels: 1 2 3 4 5

dados = data.frame(TRAT, linha, coluna, RESP)
alfa=0.05

15.4 Análise Descritiva

Media=mean(RESP)
Desvio=sd(RESP)
Variancia=var(RESP)
Maximo=max(RESP)
Minimo=min(RESP)
Mediana=median(RESP)
descritiva=cbind(Media,
                 Desvio, 
                 Variancia, 
                 Maximo, 
                 Minimo, 
                 Mediana)
kable(descritiva)

Media	Desvio	Variancia	Maximo	Minimo	Mediana
106.248	11.17751	124.9368	118.7	77.9	110.2

15.4.1 Por Tratamento

Media=tapply(RESP,TRAT, mean)
Desvio=tapply(RESP,TRAT,sd)
Variancia=tapply(RESP,TRAT, var)
Maximo=tapply(RESP,TRAT,max)
Minimo=tapply(RESP,TRAT, min)
Mediana=tapply(RESP,TRAT,median)
descritiva=cbind(Media,
                 Desvio, 
                 Variancia, 
                 Maximo, 
                 Minimo, 
                 Mediana)
kable(descritiva)

	Media	Desvio	Variancia	Maximo	Minimo	Mediana
A	88.72	9.014266	81.257	97.6	77.9	93.0
B	107.14	5.825204	33.933	114.1	100.2	108.9
C	112.10	2.636285	6.950	115.4	108.8	111.7
D	112.98	4.075782	16.612	118.7	108.6	112.0
E	110.30	10.288586	105.855	118.5	96.5	116.9

kable(round(descritiva,2), align="l")

	Media	Desvio	Variancia	Maximo	Minimo	Mediana
A	88.72	9.01	81.26	97.6	77.9	93.0
B	107.14	5.83	33.93	114.1	100.2	108.9
C	112.10	2.64	6.95	115.4	108.8	111.7
D	112.98	4.08	16.61	118.7	108.6	112.0
E	110.30	10.29	105.86	118.5	96.5	116.9

15.5 Gráfico de Caixas (Boxplot)

car::Boxplot(RESP~TRAT,
             las=1,
             col="lightblue", xlab="",
             ylab=expression("Resposta"))
points(Media,col="red", pch=8)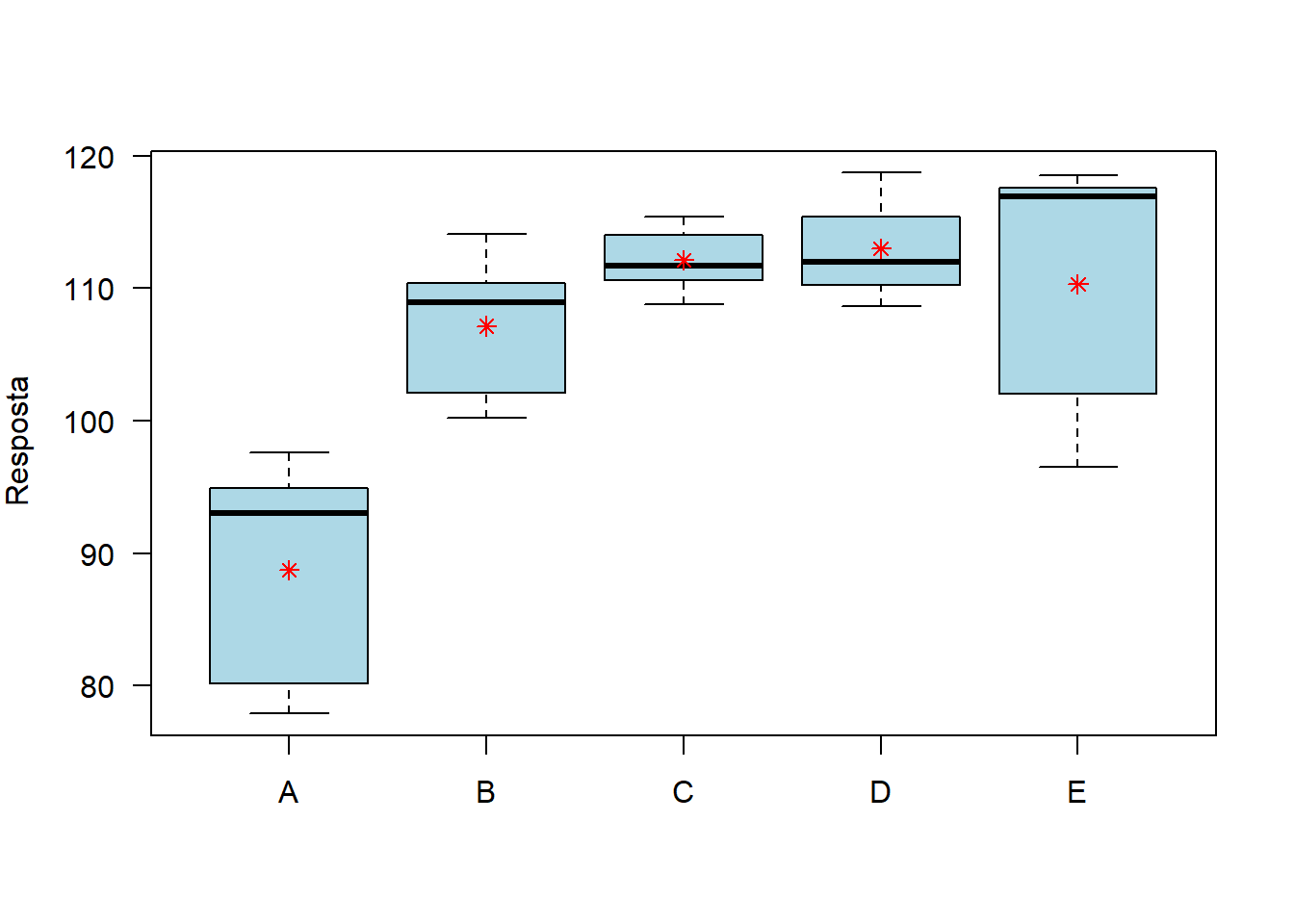

15.6 Análise de Variância

\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 = \mu_3 = \cdots = \mu_{15} \\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]

mod=aov(RESP~ TRAT+linha+coluna)
av=anova(mod)
names(av)=c("GL","SQ","QM","Teste F", "p-valor")
kable(av, align = "l", format="pandoc")

	GL	SQ	QM	Teste F	p-valor
TRAT	4	2020.0544	505.0136	9.0167153	0.0013321
linha	4	257.8264	64.4566	1.1508340	0.3796397
coluna	4	48.4984	12.1246	0.2164775	0.9241758
Residuals	12	672.1032	56.0086

Como p-valor calculado (p=\(0.0013321\)) é menor que o nível de significância adotado (\(p=0.05\)), rejeita-se \(H0\). Logo, ao menos dois tratamentos se diferem entre si

15.7 Pressuposições

15.7.1 Normalidade dos erros

\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{Os erros seguem distribuição normal}\\[.2cm] H_1: & \mbox{Os erros não seguem distribuição normal}. \end{array} \right. \end{eqnarray*}\]

(norm=shapiro.test(mod$res))

## 
##  Shapiro-Wilk normality test
## 
## data:  mod$res
## W = 0.96116, p-value = 0.438

Como p-valor calculado (p=\(0.438\)) é maior que o nível de significância adotado (\(\alpha=0.05\)), não rejeita-se \(H_O\). Logo, os erros seguem distribuição normal.

hnp::hnp(mod, las=1, xlab="Quantis teóricos", pch=16)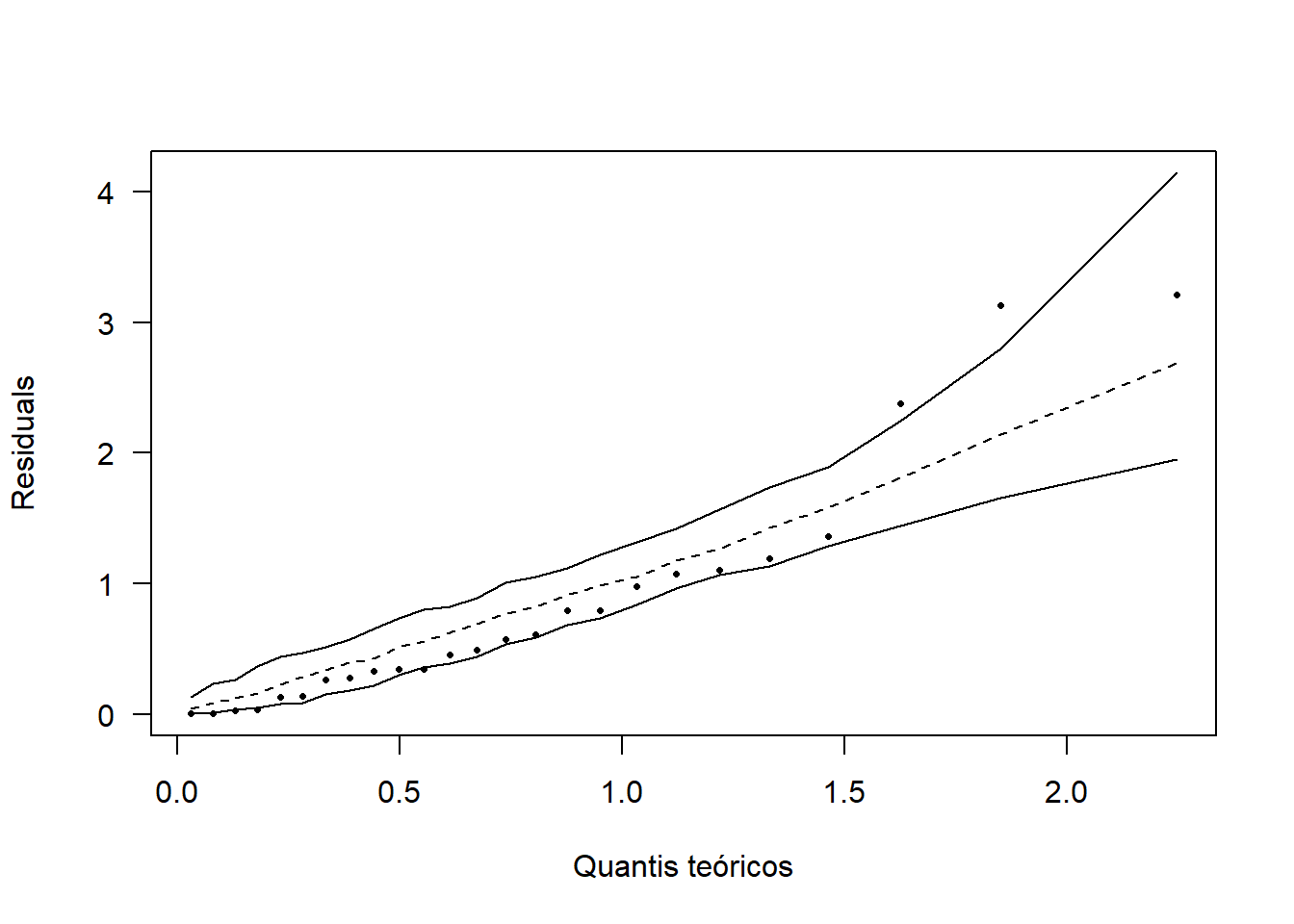

15.7.2 Homogeneidade de variâncias

\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{ As variâncias são homogêneas}\\[.2cm] H_1: & \mbox{ As variâncias não são homogêneas}. \end{array} \right. \end{eqnarray*}\]

(homog=with(dados, bartlett.test(mod$res ~ TRAT)))

## 
##  Bartlett test of homogeneity of variances
## 
## data:  mod$res by TRAT
## Bartlett's K-squared = 7.7901, df = 4, p-value = 0.09958

Como p-valor calculado (\(p=0.0996\)) é maior que o nível de significância adotado (\(p=0.05\)), não rejeita-se \(H_0\). Logo, as variâncias são homogêneas.

15.7.3 Independência dos erros

\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: \mbox{Os erros são independentes}\\[.2cm] H_1: \mbox{Os erros não são independentes}. \end{array} \right. \end{eqnarray*}\]

(ind=lmtest::dwtest(mod))

## 
##  Durbin-Watson test
## 
## data:  mod
## DW = 1.7241, p-value = 0.08134
## alternative hypothesis: true autocorrelation is greater than 0

Como p-valor calculado (p=\(0.0813\)) é maior que o nível de significância adotado (\(p=0.05\)), não rejeita-se \(H_0\). Logo, os erros são independentes.

plot(mod$res, las=1, pch=19, col='red')
abline(h=0)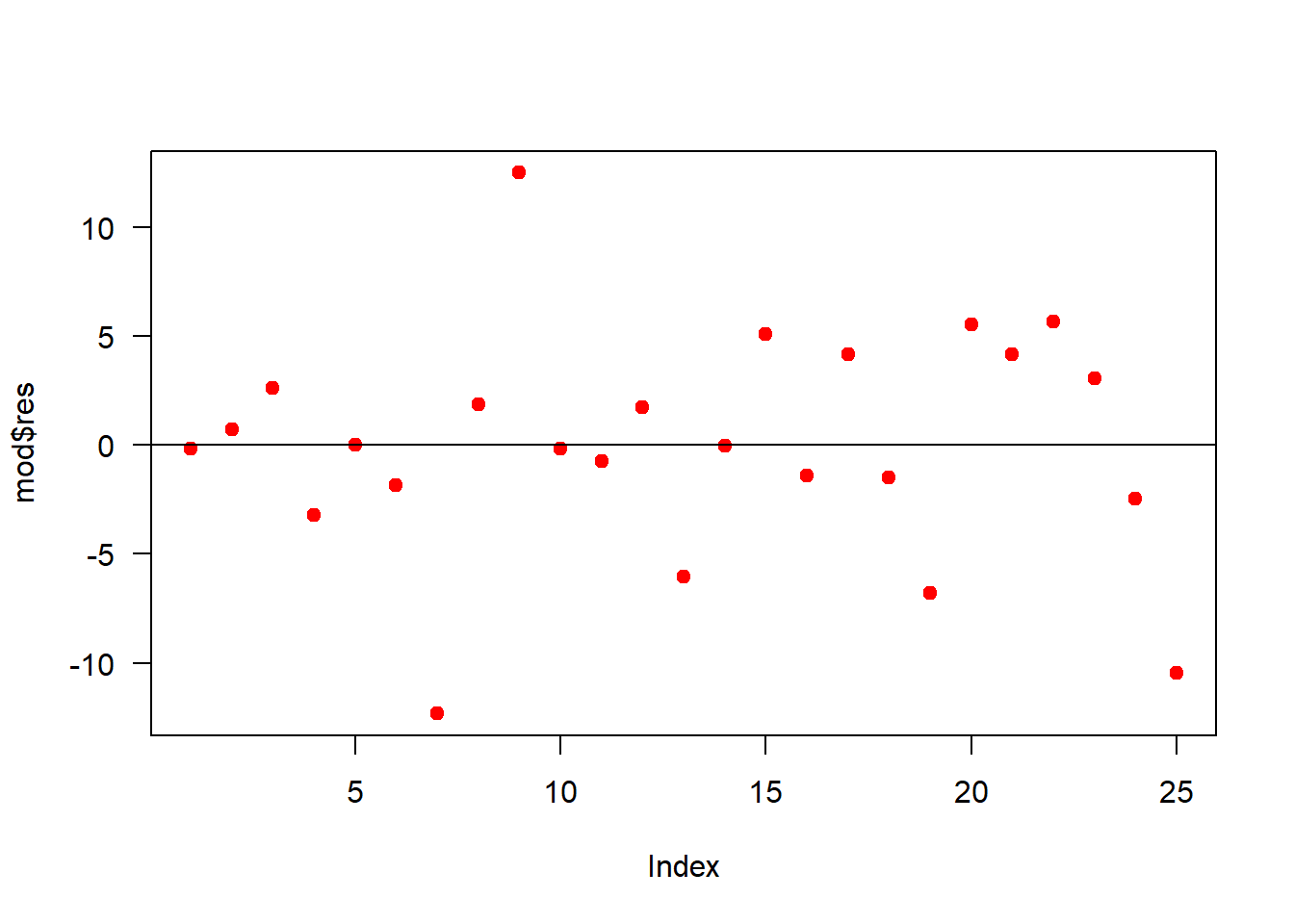

15.8 Teste de comparações

15.8.1 Usando o pacote easyanova

library(easyanova)
ea1(dados,design = 3)

## $`Analysis of variance`
##            df type III SS mean square F value    p>F
## treatments  4   2020.0544    505.0136  9.0167 0.0013
## rows        4    257.8264     64.4566  1.1508 0.3796
## columns     4     48.4984     12.1246  0.2165 0.9242
## residuals  12    672.1032     56.0086       -      -
## 
## $`Adjusted means`
##   treatment adjusted.mean standard.error tukey snk duncan t scott_knott
## 1         D        112.98         3.3469     a   a      a a           a
## 2         C        112.10         3.3469     a   a      a a           a
## 3         E        110.30         3.3469     a   a      a a           a
## 4         B        107.14         3.3469     a   a      a a           a
## 5         A         88.72         3.3469     b   b      b b           b
## 
## $`Multiple comparison test`
##     pair contrast p(tukey) p(snk) p(duncan)   p(t)
## 1  D - C     0.88   0.9997 0.8556    0.8556 0.8556
## 2  D - E     2.68   0.9776 0.8402    0.6003 0.5817
## 3  D - B     5.84   0.7332 0.6186    0.2748 0.2409
## 4  D - A    24.26   0.0019 0.0019    0.0005 0.0003
## 5  C - E     1.80   0.9949 0.7104    0.7104 0.7104
## 6  C - B     4.96   0.8286 0.5624    0.3385 0.3153
## 7  C - A    23.38   0.0026 0.0017    0.0006 0.0003
## 8  E - B     3.16   0.9598 0.5170    0.5170 0.5170
## 9  E - A    21.58   0.0048 0.0018    0.0009 0.0007
## 10 B - A    18.42   0.0150 0.0021    0.0021 0.0021
## 
## $`Residual analysis`
## $`Residual analysis`$`residual analysis`
##                               values
## p.value Shapiro-Wilk test     0.4380
## p.value Bartlett test         0.1031
## coefficient of variation (%)  7.0400
## first value most discrepant   9.0000
## second value most discrepant  7.0000
## third value most discrepant  25.0000
## 
## $`Residual analysis`$residuals
##       1       2       3       4       5       6       7       8       9      10 
##  -0.144   0.716   2.636  -3.224   0.016  -1.864 -12.324   1.856  12.496  -0.164 
##      11      12      13      14      15      16      17      18      19      20 
##  -0.744   1.756  -6.064  -0.024   5.076  -1.424   4.176  -1.484  -6.804   5.536 
##      21      22      23      24      25 
##   4.176   5.676   3.056  -2.444 -10.464 
## 
## $`Residual analysis`$`standardized residuals`
##            1            2            3            4            5            6 
## -0.027211353  0.135300893  0.498118928 -0.609231952  0.003023484 -0.352235843 
##            7            8            9           10           11           12 
## -2.328838268  0.350724101  2.361340717 -0.030990707 -0.140591989  0.331827329 
##           13           14           15           16           17           18 
## -1.145900297 -0.004535225  0.959200182 -0.269090043  0.789129228 -0.280428107 
##           19           20           21           22           23           24 
## -1.285736415  1.046125337  0.789129228  1.072580819  0.577485374 -0.461837125 
##           25 
## -1.977358296

15.8.2 Usando o pacote laercio

require(laercio)
LTukey(mod,"trat",conf.level=0.95)

## 
##  TUKEY TEST TO COMPARE MEANS 
##  
##  Confidence level:  0.95 
##  Dependent variable:  RESP
##  Variation Coefficient:  7.043793 % 
##  
## Independent variable:  TRAT 
##   Factors Means    
##   D       112.98 a 
##   C       112.1  a 
##   E       110.3  a 
##   B       107.14 a 
##   A       88.72   b
## 
##  
## Independent variable:  linha 
##   Factors Means   
##   1       109.18 a
##   4       108.6  a
##   5       107.88 a
##   2       105.12 a
##   3       100.46 a
## 
##  
## Independent variable:  coluna 
##   Factors Means   
##   1       107.74 a
##   3       107.28 a
##   5       106.56 a
##   2       105.9  a
##   4       103.76 a
## 
## 

15.8.3 Usando o pacote agricolae

require(agricolae)
TukeyHSD(mod, "TRAT", ordered = TRUE)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
##     factor levels have been ordered
## 
## Fit: aov(formula = RESP ~ TRAT + linha + coluna)
## 
## $TRAT
##      diff        lwr      upr     p adj
## B-A 18.42   3.333159 33.50684 0.0149528
## E-A 21.58   6.493159 36.66684 0.0048180
## C-A 23.38   8.293159 38.46684 0.0025698
## D-A 24.26   9.173159 39.34684 0.0019006
## E-B  3.16 -11.926841 18.24684 0.9597645
## C-B  4.96 -10.126841 20.04684 0.8286018
## D-B  5.84  -9.246841 20.92684 0.7331622
## C-E  1.80 -13.286841 16.88684 0.9949414
## D-E  2.68 -12.406841 17.76684 0.9776166
## D-C  0.88 -14.206841 15.96684 0.9996909

plot(TukeyHSD(mod, "TRAT"), col='blue', las=1)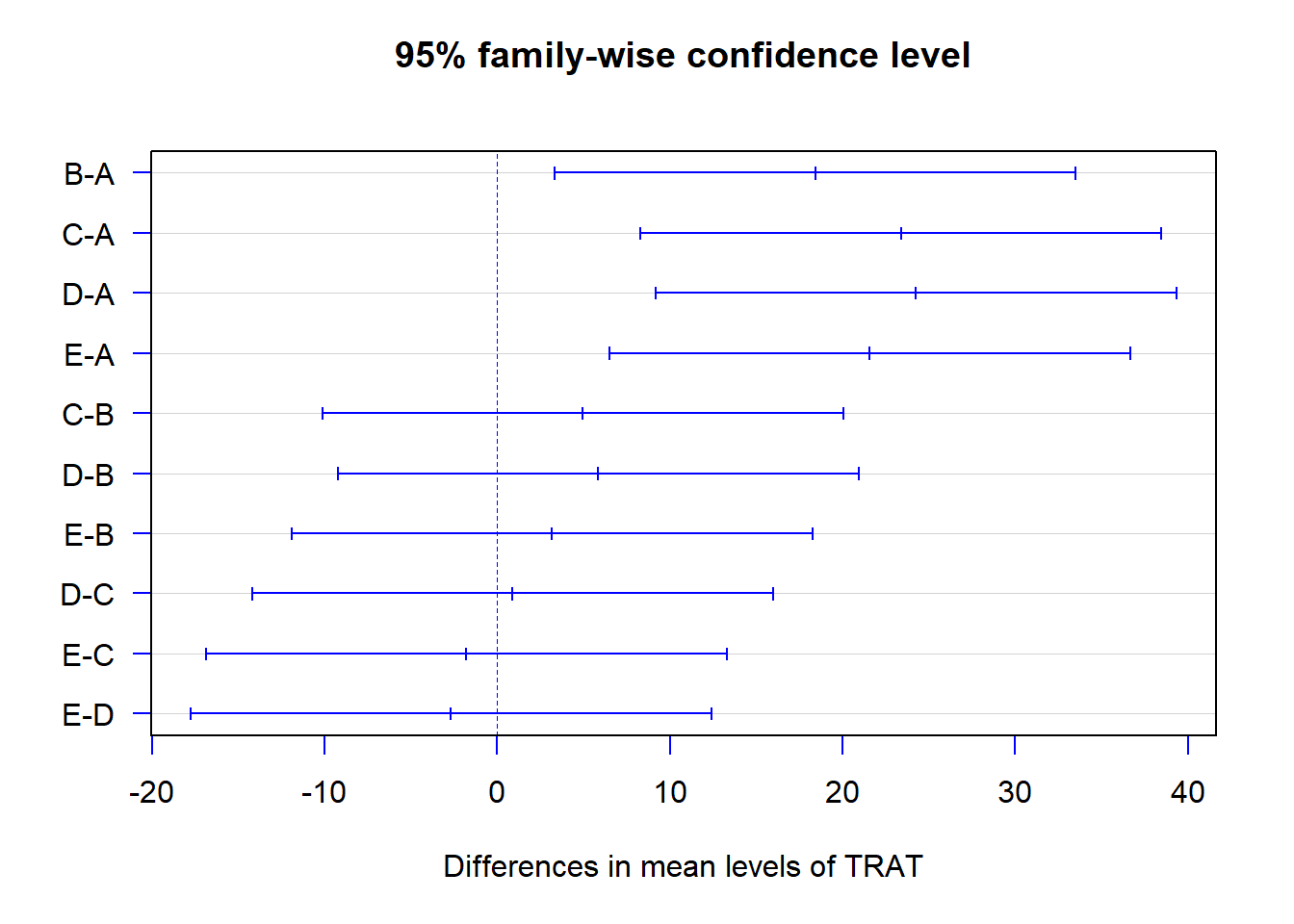

15.8.4 Usando o pacote ExpDes.pt

library(ExpDes.pt)
dql(TRAT,linha,coluna,RESP)

## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
##            GL      SQ     QM     Fc   Pr>Fc
## Tratamento  4 2020.05 505.01 9.0167 0.00133
## Linha       4  257.83  64.46 1.1508 0.37964
## Coluna      4   48.50  12.12 0.2165 0.92418
## Residuo    12  672.10  56.01               
## Total      24 2998.48                      
## ------------------------------------------------------------------------
## CV = 7.04 %
## 
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos (Shapiro-Wilk)
## valor-p:  0.4380496 
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
## 
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a     D   112.98 
## a     C   112.1 
## a     E   110.3 
## a     B   107.14 
##  b    A   88.72 
## ------------------------------------------------------------------------

---