6 Introdução à estatística
“Estatística é a Ciência que permite obter conclusões a partir de dados”
(Paul Velleman)
A Estatística (ou ciência Estatística) é um conjunto de técnicas e métodos de pesquisa que entre outros típicos envolve o planejamento do experimento a ser realizado, a coleta qualificada dos dados, a inferência, o processamento, a análise e a disseminação das informações.
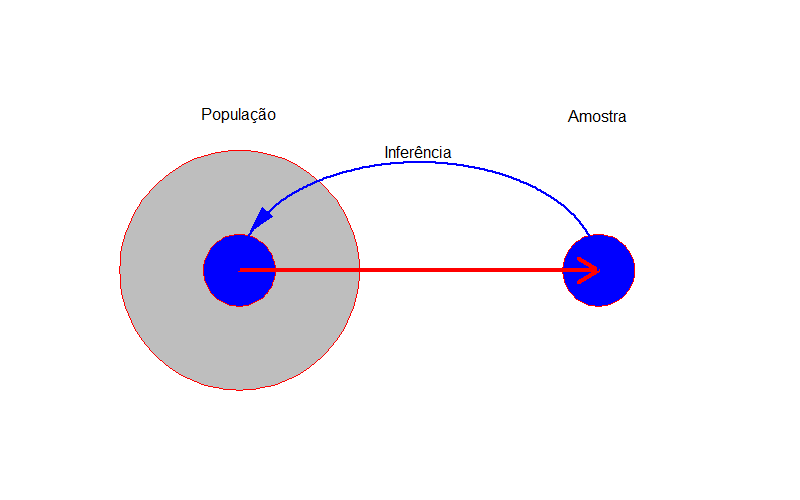
Na estatística trabalhamos com dados, nos quais podem ser obtidos por meio de uma amostra da população em estudo. Como as populações são caracterizadas por medidas numéricas descritivas, denominadas parâmetros, a inferência estatística diz respeito é realização de inferências sobre esses parâmetros populacionais. As inferências podem ser feitas por estimação de parâmetros ou por testes de hipóteses.
População: conjunto de elementos que tem pelo menos uma característica em comum. Esta característica deve delimitar corretamente quais são os elementos da população. A população pode ser classificado como:
- população ilimitada ou infinita - possui um grande número de elementos que na prática não são possíveis de serem contados.
- população limitada ou finita - possui um número determinado de elementos, possíveis de serem contados.
Amostra: subconjunto de elementos de uma população, que são representativos para estudar a característica de interesse da população. A seleção dos elementos que irão compor a amostra pode ser feita de várias maneiras e irá depender do conhecimento que se tem da população e da quantidade de recursos disponíveis.
Uma das principais subdivisões da Estatística é a AMOSTRAGEM. Que reúne os métodos necessários para coletar adequadamente amostras representativas e suficientes para que os resultados obtidos possam ser generalizados para a população de interesse
6.1 Etapas de um levantamento por amostragem
Explicitação dos objetivos com bastante clareza - para evitar dúvidas posteriores ou mesmo esquecimentos, devendo ficar bem definida qual a unidade elementar (elemento) ou unidade de análise a ser trabalhada
Definição da população a ser amostrada - em certas situações isso pode ser relativamente fácil, como no caso em que se deseja selecionar uma amostra de uma população de crianças que estejam matriculadas e frequentando certo grupo escolar.
Escolha das variáveis a serem observadas em cada unidade de análise
- Verificar todos os dados relevantes para a pesquisa e se nenhum dado foi omitido
- Existe uma tendência, particularmente ao se trabalhar com populações humanas, usando questionário, com muitas perguntas, um grande número das quais nunca analisadas
- Questionários longos, em geral, levam a diminuir a qualidade das respostas
Escolha da unidade amostral:
É a menor parte distinta e identificável da população, para fins de enumeração e sorteio da amostra
Uma unidade amostral pode ser:
- O próprio elemento de estudo
- Um conjunto de elementos.
As unidades amostrais devem cobrir toda a população e um elemento de estudo não pode pertencer ao mesmo tempo a mais de uma unidade amostral
6.2 Estatísticas e parâmetros
- Já sabemos a diferença entre amostra e população. Agora, precisamos estabelecer a distinção entre valores obtidos da amostra e valores obtidos da população;
- O parâmetro resume uma característica da população
- são valores fixos, geralmente desconhecidos e usualmente representados por caracteres gregos
Exemplos:
\(\mu\) (média populacional)
\(\sigma^2\) (variância populacional)
\(\sigma\) (desvio-padrão populacional)
\(\rho\) ou \(\pi\) proporção populacional
A estatística resume uma característica da amostra
É representada por caracteres latinos
Exemplos:
\(\bar{X}\) (média amostral)
\(S^2\) (variância amostral)
\(S\) (desvio-padrão amostral)
\(\hat{p}\) ou \(\hat{\pi}\) (proporção amostral)
6.3 Tamanho Amostral
DETERMINAÇÃO DO TAMANHO DE UMA AMOSTRA COM BASE NA ESTIMATIVA DA MÉDIA POPULACIONAL
A determinação do tamanho de uma amostra é problema de grande importância, porque: - amostras desnecessariamente grandes acarretam desperdício de tempo e de dinheiro; - e amostras excessivamente pequenas podem levar a resultados não confiáveis.
Em muitos casos é possível determinar o tamanho mínimo de uma amostra para estimar um parâmetro estatístico, como por exemplo, a MÉDIA POPULACIONAL (\(\mu\)).
A fórmula para cálculo do tamanho da amostra para uma estimativa confiável da MÉDIA POPULACIONAL (\(\mu\)) é dada por:
em que:
- n = número de indivíduos na amostra
- \(Z_{\alpha/2}\) = Valor crítico que corresponde ao grau de confiança desejado.
- \(\sigma\) = Desvio-padrão populacional da variável estudada.
- \(e\) = Margem de erro ou ERRO MÁXIMO DE ESTIMATIVA. Identifica a diferença máxima entre a MÉDIA AMOSTRAL ( X ) e a verdadeira MÉDIA POPULACIONAL
Os valores de confiança mais utilizados e os valores de Z:
- Grau de confiança:90%,\(\alpha\)=0,10, Valor crítico \(Z_{\alpha/2}\)=1,645
- Grau de confiança:95%,\(\alpha\)=0,05, Valor crítico \(Z_{\alpha/2}\)=1,96
- Grau de confiança:99%,\(\alpha\)=0,01, Valor crítico \(Z_{\alpha/2}\)=2,575
DETERMINAÇÃO DO TAMANHO DE UMA AMOSTRA COM DESVIO-PADRÃO DESCONHECIDO
Não conhecendo o desvio-padrão da população, substituímos \(\sigma\) por sua estimativa \(s\) e usamos a distribuição t de Student. Porém, se ainda não retiramos a amostra como teremos o \(s\)?
Se \(n \leq n'\), a amostra-piloto já terá sido suficiente para a estimação. Caso contrário, deveremos retirar, ainda, da população, os elementos necessários à complementação do tamanho mínimo da amostra.
Tipos de Amostragem
- Para se obter uma amostra, é preciso definir os critérios que serão usados para selecionar as unidades que irão compor essa amostra
- De acordo com a técnica usada, podem ser realizados três tipos de amostragem:
Amostragem aleatória, casual ou probabilística
- Aleatória simples
- Estratificada
Amostragem semiprobabilística
- Sistemática
- Por conglomerados
- Por cotas
Amostragem não-probabilística ou de conveniência
Amostragem simples
- É constituída por n unidades retiradas ao acaso da população de tamanho N;
- Toda unidade da população tem probabilidade conhecida \(\frac{n}{N}\) de pertencer à amostra;
- Para obter uma amostra aleatória simples - a população deve ser conhecida e cada unidade identificada por nome ou por número;
- Os elementos que constituirão a amostra serão escolhidos por sorteio, que pode ser feito usando-se um software estatístico
- Na maioria das vezes, usa-se a amostragem sem reposição
Amostragem aleatória estratificada
- é usada quando a população é constituída por unidades heterogêneas para a variável que se quer estudar
- As unidades da população de tamanho N, devem ser identificadas e depois as unidades similares devem ser reunidas em subgrupos chamados estratos de tamanhos \(N_1, N_2, ..., N_k\)
- em que \(N_1 + N_2 + : : : + N_k = N\)
- Exemplos de estratos:
- sexo
- renda
- idade, etc
- O sorteio dos elementos da amostra é feito dentro de cada estrato
- Se a população é composta de k estratos:
- N é o tamanho da população
- Nh é o tamanho de cada estrato populacional
- n é o tamanho total da amostra
- nh é o tamanho da amostra do estrato h, e \(n1 + n2 + : : : nk = n\)
Amostragem sistemática
- Para realizar a amostragem sistemática é preciso que a população esteja organizada em:
- filas
- arquivos
- domicílios de uma cidade, etc
- Por exemplo, para tomar uma amostra dos domicílios de uma cidade, parte-se de um ponto sorteado e toma-se, de tantos em tantos, um domicílio para a amostra.
- Devido a sua simplicidade operacional - a amostragem sistemática é amplamente adotada para o sorteio de amostras estratificadas sob o critério de proporcionalidade
- Na amostragem sistemática, os N elementos da população são reunidos em grupos definidos por um intervalo de amplitude j = N=n
- Desse intervalo, deve ser sorteado um elemento de cada grupo para compor a amostra
Amostragem por conglomerado
- A população é dividida em subpopulações (conglomerados) distintas
- Asilo
- Quarteirões
- Residências
- Famílias
- Universidade
- Serviço militar
- Bairros, etc
- Esse tipo de amostragem é realizado em duas etapas
- Primeira etapa - Um subconjunto dos conglomerados é aleatoriamente escolhido;
- Segunda etapa - Para cada conglomerado selecionado é escolhida uma amostra aleatória simples para ser incluída na amostra aleatória final, ou quando possível analisam-se todos os indivíduos pertencentes aos conglomerados selecionados;
- Esse tipo de amostragem é menos eficiente que a amostragem aleatória simples ou amostragem estratificada. Porém, é um tipo de amostragem mais econômica;
- Esse procedimento amostral é adequado quando é possível dividir a população em um grande número de pequenas subpopulações.
Amostragem por cotas
- A idéia de cota é semelhante à de estrato, com uma diferença básica: a amostra é selecionada por julgamento e depois confirmadas as características das unidades a amostradas;
- A amostragem por cotas não é feita de forma aleatória;
- A vantagem é ser relativamente barata, e por esta razão é muito usada em levantamentos de opinião e pesquisa de mercado;
- É constituída por n unidades retiradas da população de tamanho N segundo cotas estabelecidas de acordo com a distribuição desses elementos na população;
- A amostra por cotas exige algum conhecimento da população, mas as unidades não precisam estar numeradas ou identificadas
Amostra não-probabilística ou de conveniência
- A amostragem não-probabilística pode prejudicar sensivelmente a validade de um estudo
- Isso ocorre porque muitos fatores podem influir na escolha de uma unidade amostral para pertencer à amostra
- Isso prejudica a sua representatividade em relação à população
- Existem situações em que ela é (ou necessita) ser utilizada