16 Esquema Fatorial (2 Fatores)
Nos experimentos mais simples comparamos níveis (tratamentos) de apenas um fator; Entretanto, existem casos em que dois ou mais fatores devem ser estudados simultaneamente para que possam nos conduzir a resultados de interesse;
Em geral, os experimentos fatoriais são mais eficientes para este tipo de experimento, pois estudam, ao mesmo tempo, os efeitos de dois ou mais fatores, cada um deles com dois ou mais níveis.
O fatorial é um tipo de esquema, ou seja, uma das maneiras de organizar os tratamentos e não um tipo de delineamento;
Os experimentos fatoriais são montados segundo um tipo de delineamento experimental;
Nos experimentos fatoriais, os tratamentos são obtidos pelas combinações dos níveis dos fatores.
16.1 Tipos de efeitos avaliados
Efeito Principal: é o efeito de cada fator, independente do efeito dos outros fatores;
Efeito de Interação: é o efeito simultâneo dos fatores sobre a variável em estudo. Dizemos que ocorre interação entre os fatores quando os efeitos dos níveis de um fator são modificados pelos níveis do outro fator.
16.2 Vantagens
Pode-se estudar dois ou mais fatores num único experimento.
Pode-se, por meio dos efeitos das interações, verificar se um fator é independente ou dependente do(s) outro(s).
16.3 Desvantagens
O número de tratamentos ou combinações de níveis de fatores cresce, rapidamente, com o aumento do número de níveis, em cada fator, ou mesmo com o aumento do número de fatores.
A interpretação dos resultados se torna mais difícil é medida que aumentamos o número de níveis e de fatores no experimento.
16.4 Modelo estatístico
As observações podem ser descritas pelo modelo estatístico linear:
\(y_{ij} = \mu+\tau_{i}+\beta_{j}+(\tau\beta)_{ij}+\epsilon_{ij}\)
- i = 1; 2; : : : ; a
- j = 1; 2; : : : ; b
- k = 1; 2; : : : ; r
em que:
- \(y_{ijk}\) é o valor observado no i-ésimo nivel do Fator A e j-ésima nível do Fator B;
- \(\mu\) é uma constante;
- \(\tau_{i}\) é o efeito do i-ésimo nível do fator A;
- \(\beta_{j}\) é o efeito do j-ésimo nível do fator B;
- \((\tau\beta)_ij\) é o efeito da interação entre \(\tau_{i}\) e \(\beta_{j}\);
- \((\epsilon)ijk\) é o componente de erro aleatório.
16.5 Hipóteses e quadro da análise de variância
No experimento fatorial com 2 fatores, deseja-se testar a signicância de ambos os fatores.
Há interesse em testar hipóteses sobre a igualdade dos efeitos do fator A, isto é:
- H0 : \(\beta_{11}\) = \(\beta_{12}\) = : : : \(\beta_{1a}\) = 0
- H1 : Pelo menos um \(\beta_{1i} \neq 0\)
e a igualdade nos efeitos do fator B, ou seja:
- H0 : \(\beta_{21}\) = \(\beta_{22}\) = : : : \(\beta_{2b}\) = 0
- H1 : Pelo menos um \(\beta_{2j} \neq 0\)
e, ainda, se há interação entre os fatores:
- H0 : \((\beta_1\beta_2)_{ij}\) = 0 para todo i ; j
- H1 : Pelo menos um \((\beta_1\beta_2)_{ij} \neq 0\)
| CV | G.L. | S.Q. | Q.M. | Fcalc |
|---|---|---|---|---|
| Fator A | \(a - 1\) | \(SQ_{A}\) | \(\frac{SQ_{A}}{a-1}\) | \(\frac{QM_{A}}{QM_{Res}}\) |
| Fator B | \(b-1\) | \(SQ_{B}\) | \(\frac{SQ_{B}}{b-1}\) | \(\frac{QM_{B}}{QM_{Res}}\) |
| Interação A x B | \((a-1)(b-1)\) | \(SQ_{AxB}\) | \(\frac{SQ_{AxB}}{(a-1)(b-1)}\) | \(\frac{QM_{AxB}}{QM_{Res}}\) |
| resíduo | \(ab(n-1)\) | \(SQ_{Res}\) | \(\frac{SQ_{Res(b)}}{ab(n-1)}\) | |
| Total | \(abn-1\) | \(SQ_{Total}\) | - |
16.6 Croqui em DIC
Criando uma função para fazer um croqui (Número de coluna igual número de repetições)
# Não alterar os comandos da função
library(agricolae)
library(gridExtra)
library(grid)
croqui=function(trat,r){
sort=design.ab(trat,r,design = "crd",serie=0)
sort$book$trat=as.vector(matrix(paste(sort$book$A,sort$book$B),nrow =r,byrow=T))
ncol=r
sort$book$trat=as.factor(sort$book$trat)
gs <- lapply(sort$book$trat, function(ii)
grobTree(rectGrob(gp=gpar(fill=ii, alpha=0.5)),textGrob(ii)))
grid.arrange(grobs=gs, ncol=ncol)}Vetor de tratamentos
trat=c(2,2)Usando a função
croqui(trat,r=3)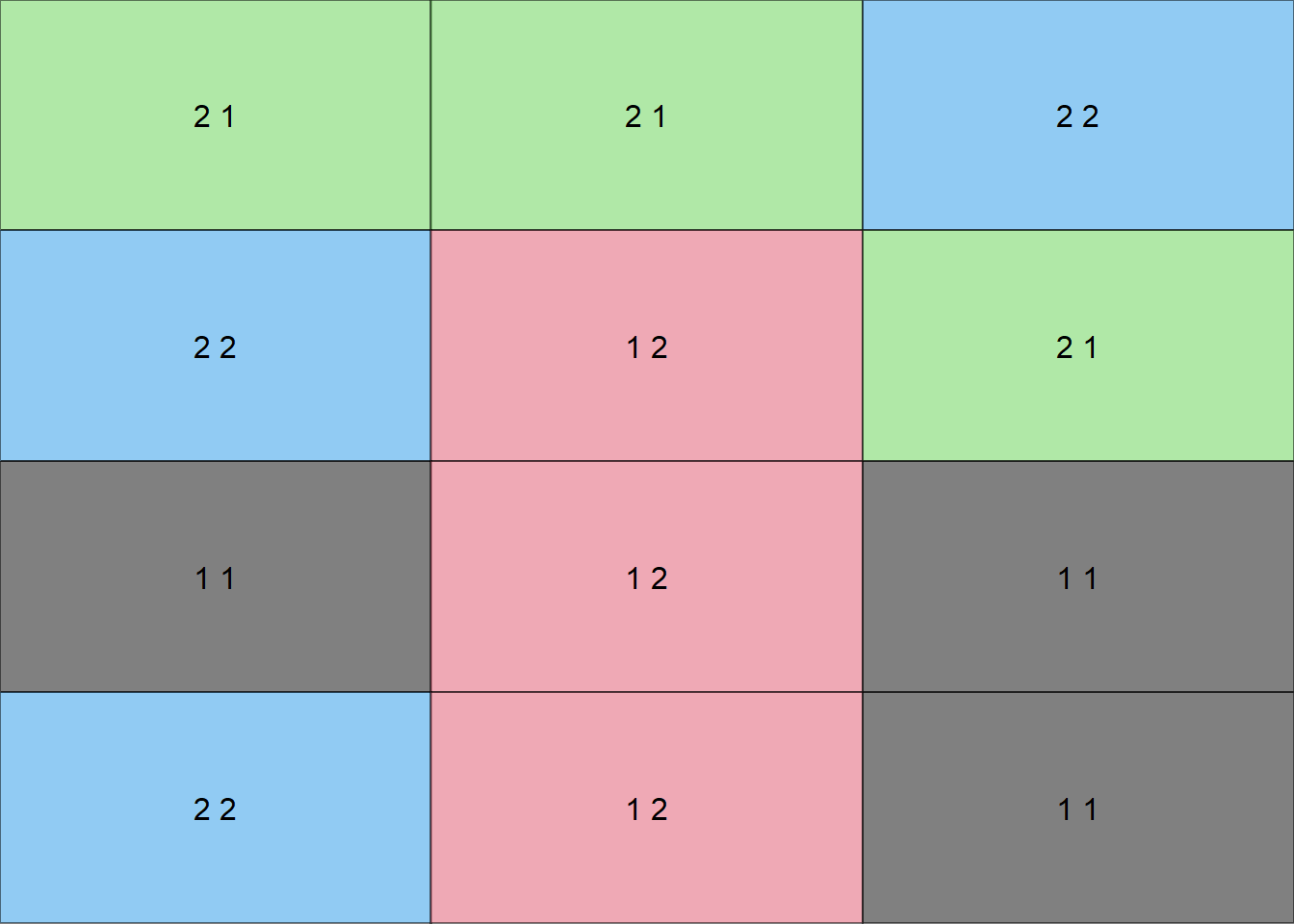
Criando uma função para fazer um croqui (Número de colunas igual número de tratamentos)
# Não alterar os comandos da função
library(agricolae)
library(gridExtra)
library(grid)
croqui=function(trat,r){
sort=design.ab(trat,r,design = "crd",serie=0)
sort$book$trat=as.vector(t(matrix(paste(sort$book$A,sort$book$B),nrow =r, byrow=T)))
sort$book$trat=as.factor(sort$book$trat)
ncol=length(levels(sort$book$trat))
gs <- lapply(sort$book$trat, function(ii)
grobTree(rectGrob(gp=gpar(fill=ii, alpha=0.5)),textGrob(ii)))
grid.arrange(grobs=gs, ncol=ncol)}Vetor de tratamentos
trat=c(2,2) # número de níveis do fator 1 e fator 2 (no caso são 2 cada)Usando a função
croqui(trat,r=3)
16.7 Croqui em DBC
Criando uma função para fazer um croqui (Número de coluna igual número de repetições)
# Não alterar os comandos da função
library(agricolae)
library(gridExtra)
library(grid)
croqui=function(trat,r){
sort=design.ab(trat,r,design = "rcbd",serie=0)
sort$book$trat=as.vector(matrix(paste(sort$book$A,sort$book$B),nrow =r,byrow=T))
ncol=r
sort$book$trat=as.factor(sort$book$trat)
gs <- lapply(sort$book$trat, function(ii)
grobTree(rectGrob(gp=gpar(fill=ii, alpha=0.5)),textGrob(ii)))
grid.arrange(grobs=gs, ncol=ncol)}Vetor de tratamentos
trat=c(2,2)Usando a função
croqui(trat,r=3)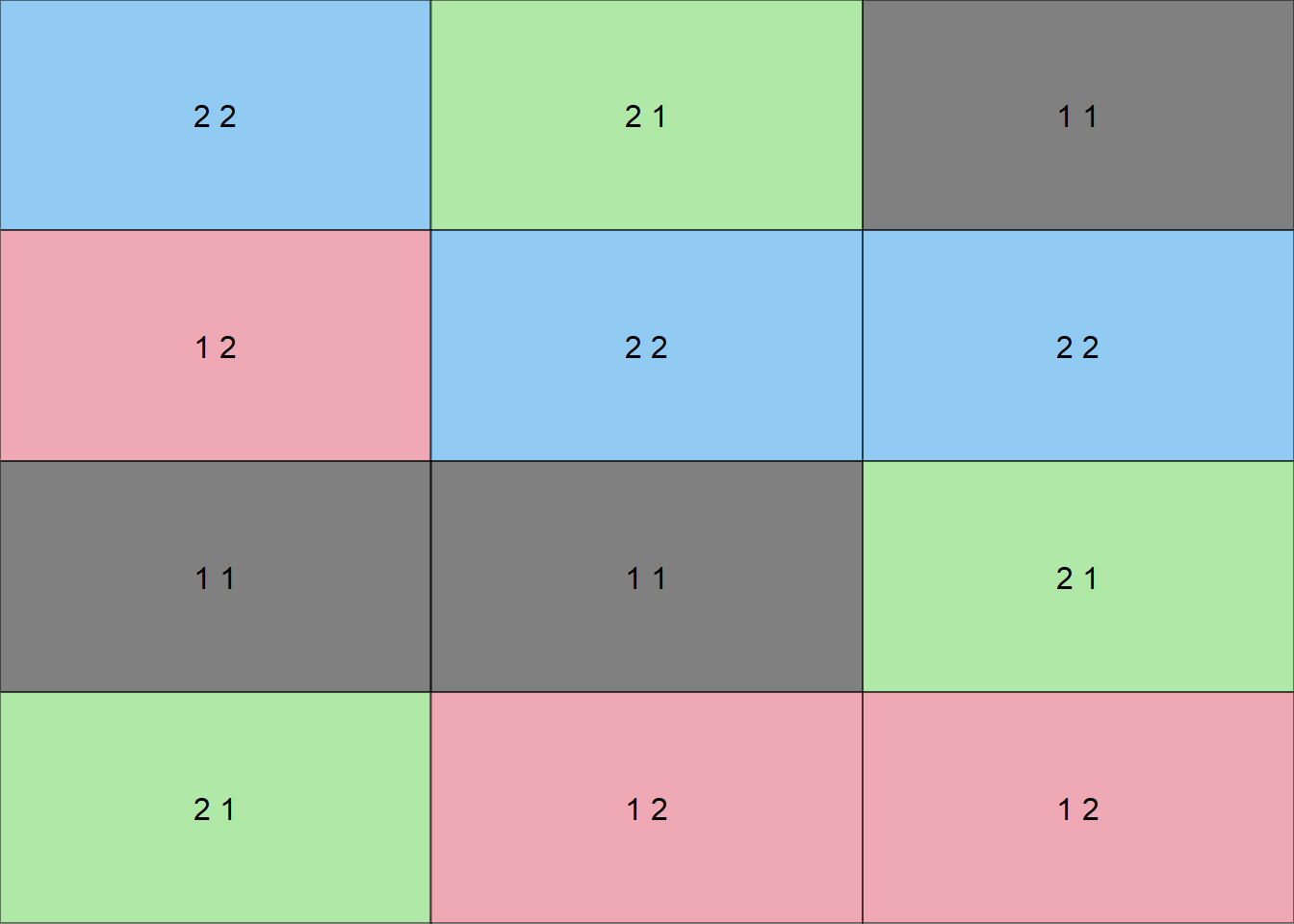
Criando uma função para fazer um croqui (Número de colunas igual número de tratamentos)
# Não alterar os comandos da função
library(agricolae)
library(gridExtra)
library(grid)
croqui=function(trat,r){
sort=design.ab(trat,r,design = "rcbd",serie=0)
sort$book$trat=as.vector(t(matrix(paste(sort$book$A,sort$book$B),nrow =r, byrow=T)))
sort$book$trat=as.factor(sort$book$trat)
ncol=length(levels(sort$book$trat))
gs <- lapply(sort$book$trat, function(ii)
grobTree(rectGrob(gp=gpar(fill=ii, alpha=0.5)),textGrob(ii)))
grid.arrange(grobs=gs, ncol=ncol)}Vetor de tratamentos
trat=c(2,2) # número de níveis do fator 1 e fator 2 (no caso são 2 cada)Usando a função
croqui(trat,r=3)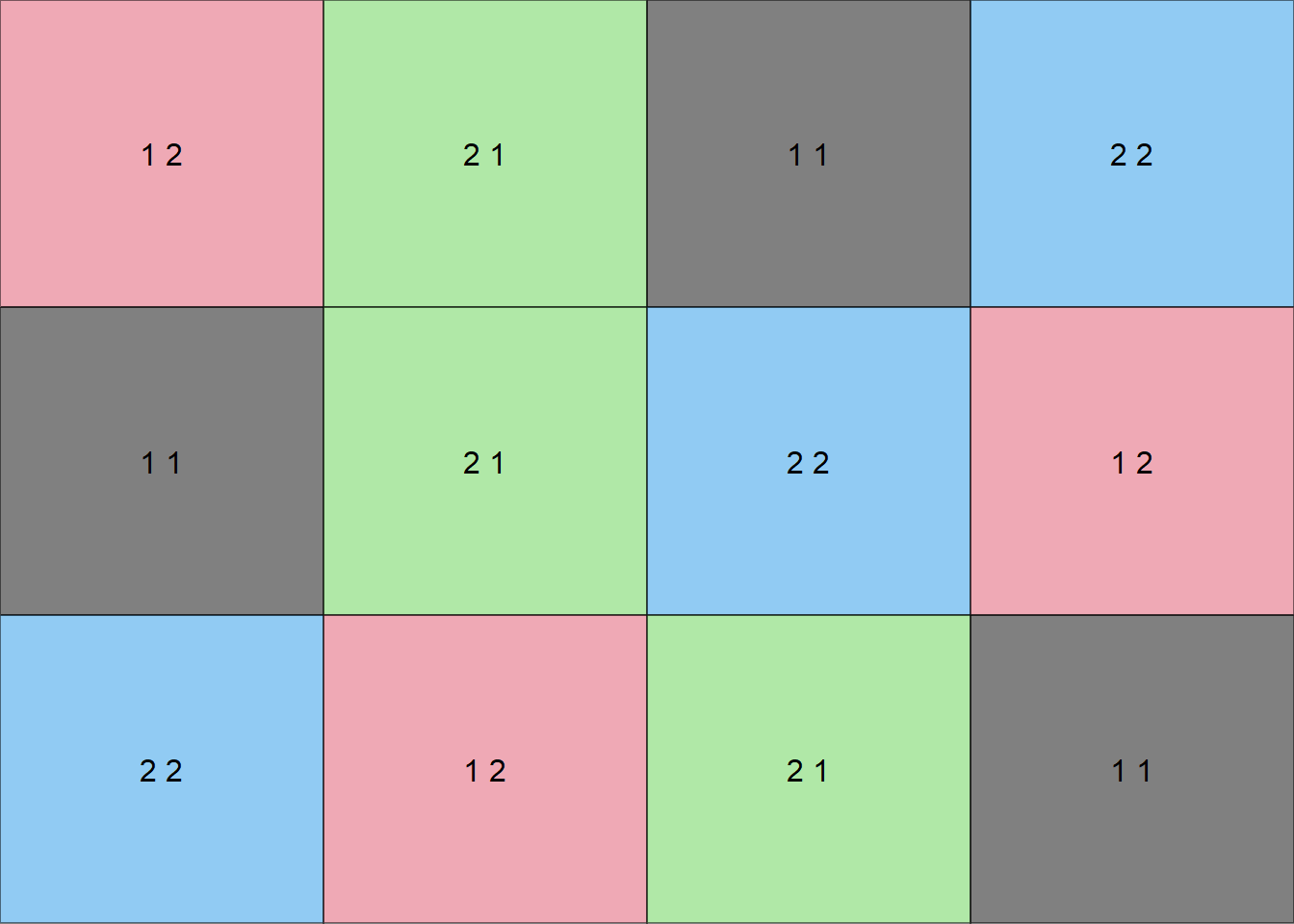
16.8 Exemplo 1 (Fatorial duplo em DIC)
Um experimento foi conduzido em casa de vegetação em vasos na Universidade Estadual de Londrina. O trabalho tem o objetivo de avaliar a aplicação de dicloroisocianurato de sódio (DUP) em soja em 4 épocas de aplicação em soja inoculada ou não com Rhizobium e sua influência sobre o número de nódulos. O experimento foi conduzido em delineamento inteiramente casualizado com cinco repetições.

Fonte da foto: https://blog.aegro.com.br/inoculante-para-soja/
NN=c(339,332,163,230,300,
163,172,123,083,161,
171,069,095,046,079,
335,235,217,174,222,
284,136,225,098,110,
082,038,092,053,046,
196,252,346,468,258,
032,038,063,048,160)
(Inoculacao=rep(c("IN","NI"),e=20))## [1] "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN"
## [16] "IN" "IN" "IN" "IN" "IN" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI"
## [31] "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI"(epoca=rep(c("Plantio","V1+15","V3+15","R1+15"),e=5,2))## [1] "Plantio" "Plantio" "Plantio" "Plantio" "Plantio" "V1+15" "V1+15"
## [8] "V1+15" "V1+15" "V1+15" "V3+15" "V3+15" "V3+15" "V3+15"
## [15] "V3+15" "R1+15" "R1+15" "R1+15" "R1+15" "R1+15" "Plantio"
## [22] "Plantio" "Plantio" "Plantio" "Plantio" "V1+15" "V1+15" "V1+15"
## [29] "V1+15" "V1+15" "V3+15" "V3+15" "V3+15" "V3+15" "V3+15"
## [36] "R1+15" "R1+15" "R1+15" "R1+15" "R1+15"F1=as.factor(Inoculacao)
F2=as.factor(epoca)
Trat=paste(F1,F2)
dados=data.frame(F1,F2,resp=NN)
X="";Y="Número de nódulos"16.9 Estatística descritiva
Media = with(dados, mean(resp))
Variancia = with(dados, var(resp))
Desvio = with(dados, sd(resp))
CV = Desvio / Media * 100
desc = cbind(Media, Variancia, Desvio, CV)
desc| Media | Variancia | Desvio | CV |
|---|---|---|---|
| 168.35 | 11413.41 | 106.83 | 63.46 |
16.9.1 Por Inoculação
MediaA = with(dados, tapply(resp, F1, mean))
VarianciaA = with(dados, tapply(resp, F1, var))
DesvioA = with(dados, tapply(resp, F1, sd))
CVA = DesvioA / MediaA * 100
Desc = cbind(MediaA, VarianciaA, DesvioA, CVA)
Desc| MediaA | VarianciaA | DesvioA | CVA | |
|---|---|---|---|---|
| IN | 185.45 | 8229.21 | 90.71 | 48.92 |
| NI | 151.25 | 14582.72 | 120.76 | 79.84 |
16.9.2 Por época de aplicação
MediaB = with(dados, tapply(resp, F2, mean))
VarianciaB = with(dados, tapply(resp, F2, var))
DesvioB = with(dados, tapply(resp, F2, sd))
CVB = DesvioB / MediaB * 100
Desc = cbind(MediaB, VarianciaB, DesvioB, CVB)
Desc| MediaB | VarianciaB | DesvioB | CVB | |
|---|---|---|---|---|
| Plantio | 221.7 | 8287.34 | 91.03 | 41.06 |
| R1+15 | 152.4 | 10686.93 | 103.38 | 67.83 |
| V1+15 | 101.3 | 2559.12 | 50.59 | 49.94 |
| V3+15 | 198.0 | 18507.56 | 136.04 | 68.71 |
16.10 Gráficos exploratórios
16.10.1 Gráfico de Caixas
16.10.1.1 Fator 1
par(bty='l', mai=c(1, 1, .2, .2))
par(cex=0.7)
caixas=with(dados, car::Boxplot(resp ~ F1, vertical=T,las=1, col='Lightyellow',
xlab=X, ylab=Y))
mediab=with(dados,tapply(resp, F1, mean))
points(mediab, pch='+', cex=1.5, col='red')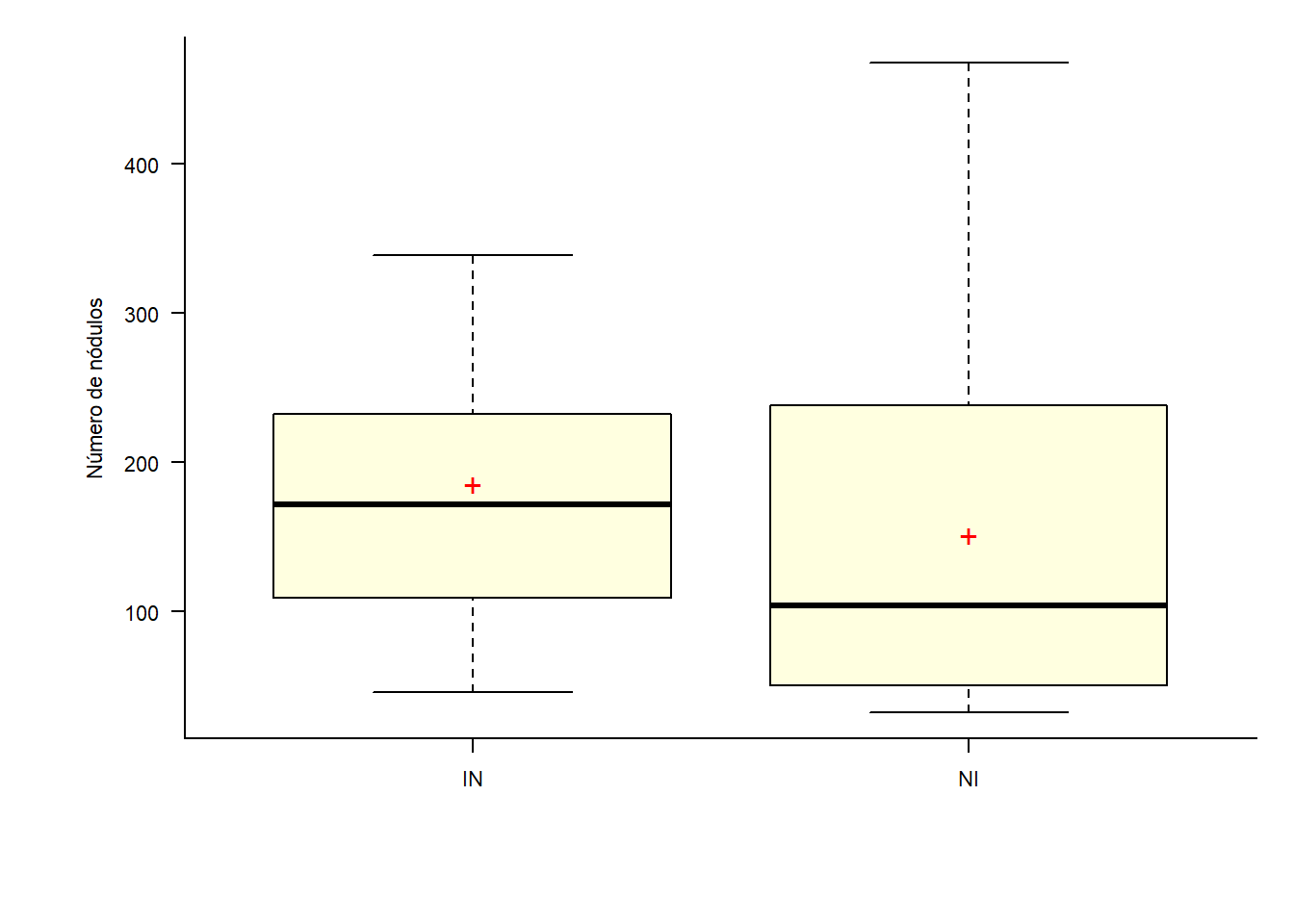
16.10.1.2 Fator 2
par(bty='l', mai=c(1, 1, .2, .2))
par(cex=0.7)
caixas=with(dados, car::Boxplot(resp ~ F2, vertical=T,las=1, col='Lightyellow',
xlab=X, ylab=Y))
mediab=with(dados,tapply(resp, F2, mean))
points(mediab, pch='+', cex=1.5, col='red')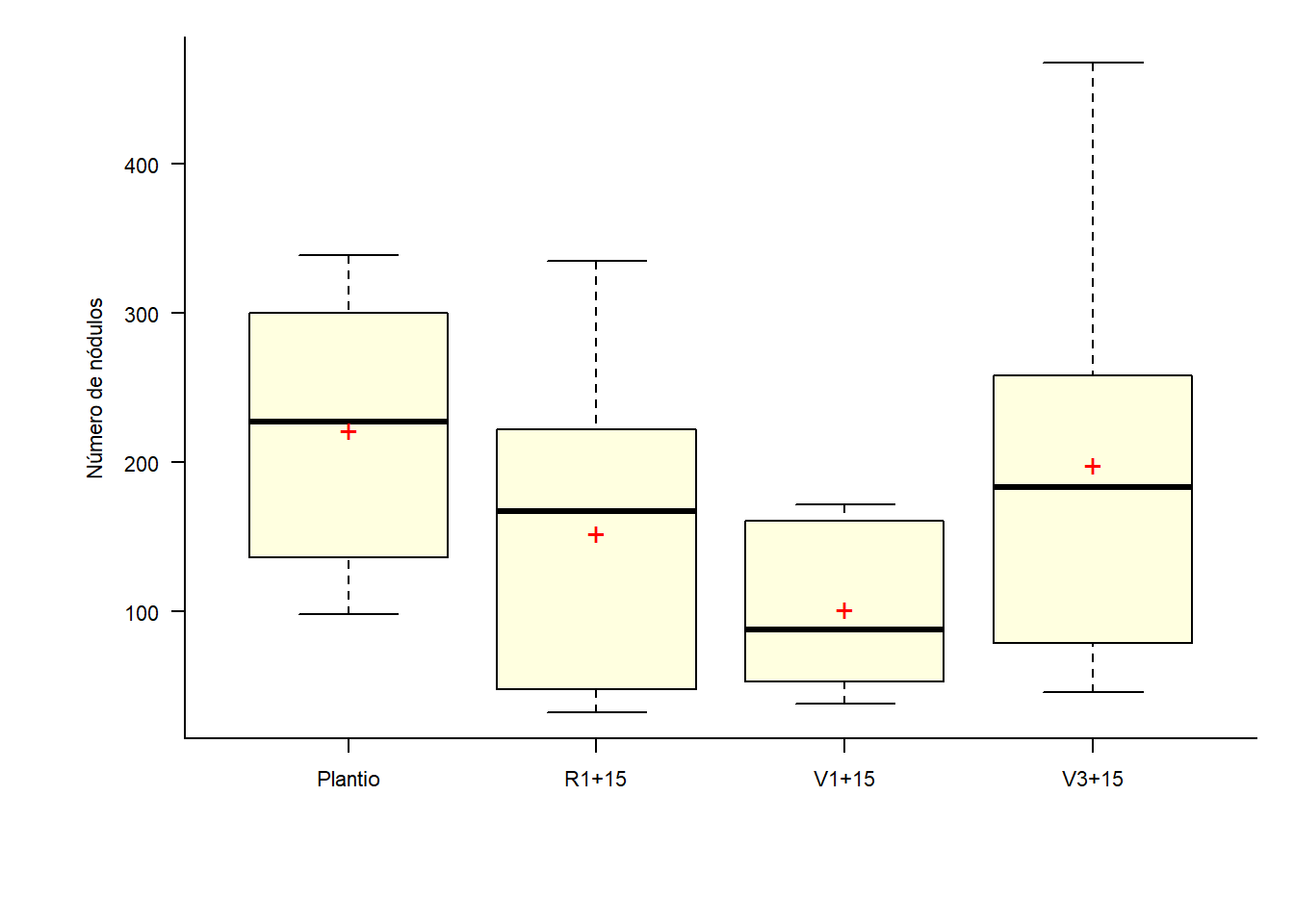
16.10.1.3 Juntando Fatores
par(bty='l', mai=c(1, 1, .2, .2))
par(cex=0.7)
caixas=with(dados, car::Boxplot(resp ~ F1*F2, vertical=T,las=1, col='Lightyellow',
xlab=X, ylab=Y))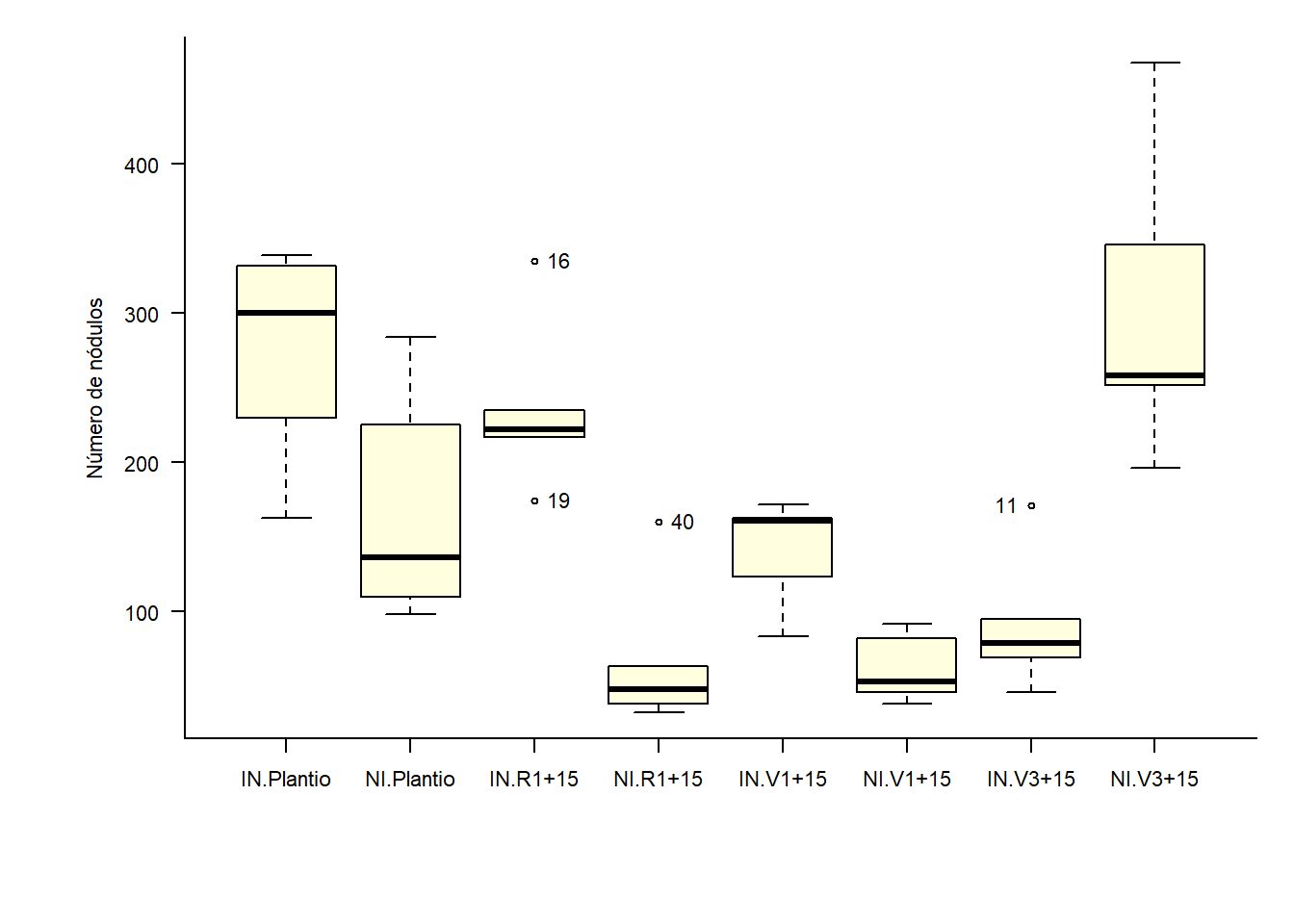
16.10.2 Gráfico de interação
with(dados, interaction.plot(F2, F1, resp, las=1, col=1:6, bty='l',
xlab='', ylab='CBM', trace.label="FATOR1"))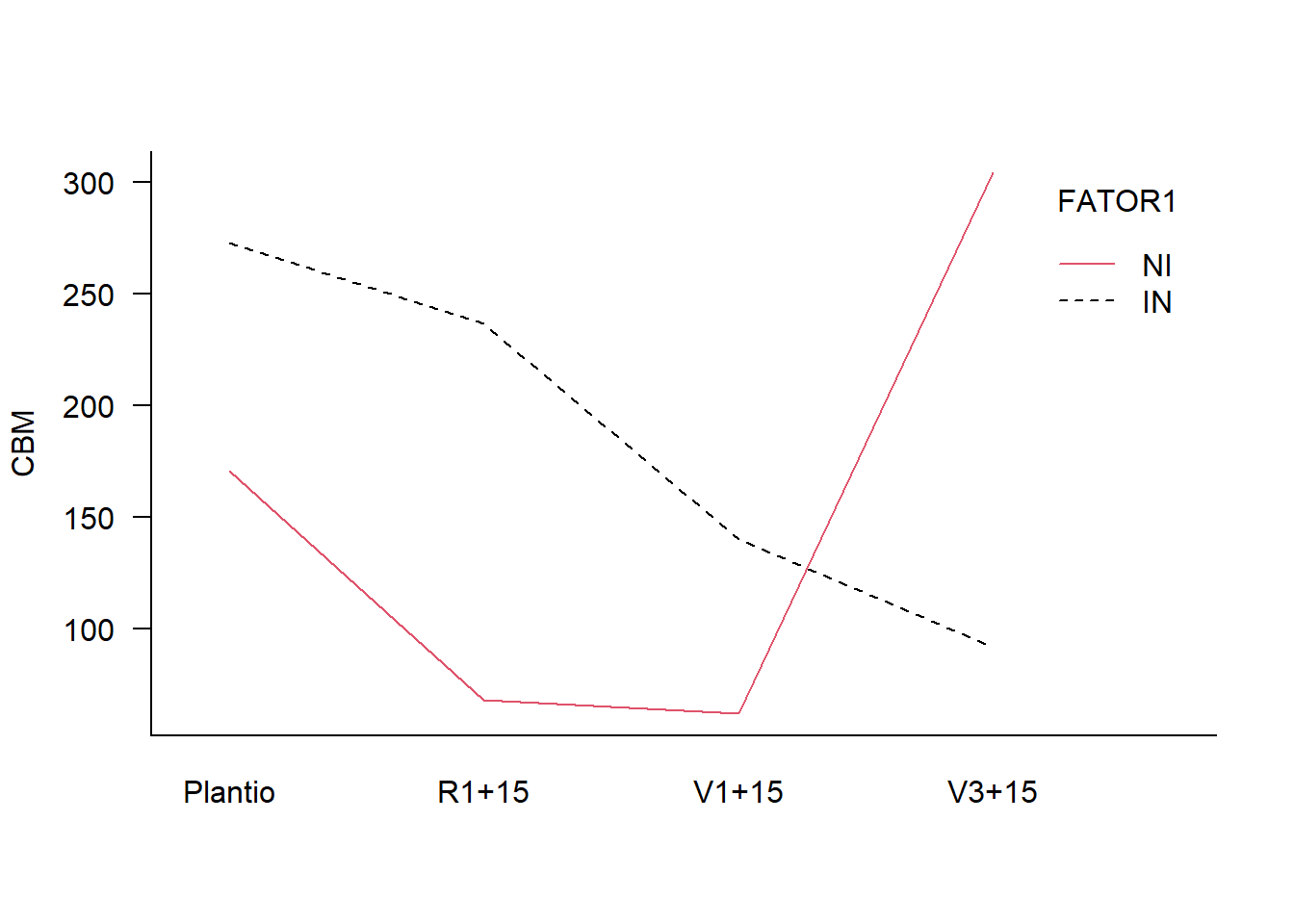
# FATOR1 e FATOR2
with(dados, interaction.plot(F1, F2, resp, las=1, col=1:6, bty='l',
xlab='', ylab='CBM', trace.label="FATOR2"))
16.11 Análise de Variância
Hipótese do Fator 1:
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2\\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
Hipótese do Fator 2:
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 = \mu_3 = \mu_4 \\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
Hipótese da interação:
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{Todas as combinações entre os níveis do fator 1 e do fator 2 têm o mesmo efeito} \\[.2cm] H_1: & \mbox{Pelo menos duas combinações entre os níveis do fator 1 e do fator 2 têm efeitos diferentes}. \end{array} \right. \end{eqnarray*}\]
mod = with(dados, aov(resp~F1*F2))
anova(mod)| GL | SQ | QM | Teste F | p-valor | |
|---|---|---|---|---|---|
| F1 | 1 | 11696.4 | 11696.40 | 2.757934 | 0.1065420 |
| F2 | 3 | 84754.5 | 28251.50 | 6.661518 | 0.0012721 |
| F1:F2 | 3 | 212960.2 | 70986.73 | 16.738206 | 0.0000010 |
| Residuals | 32 | 135712.0 | 4241.00 |
16.12 Pressuposições
16.12.1 Normalidade dos erros
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{Os erros seguem distribuição normal}\\[.2cm] H_1: & \mbox{Os erros não seguem distribuição normal}. \end{array} \right. \end{eqnarray*}\]
(norm=shapiro.test(mod$res))##
## Shapiro-Wilk normality test
##
## data: mod$res
## W = 0.96809, p-value = 0.3125hnp::hnp(mod, las=1, xlab="Quantis teóricos", pch=16)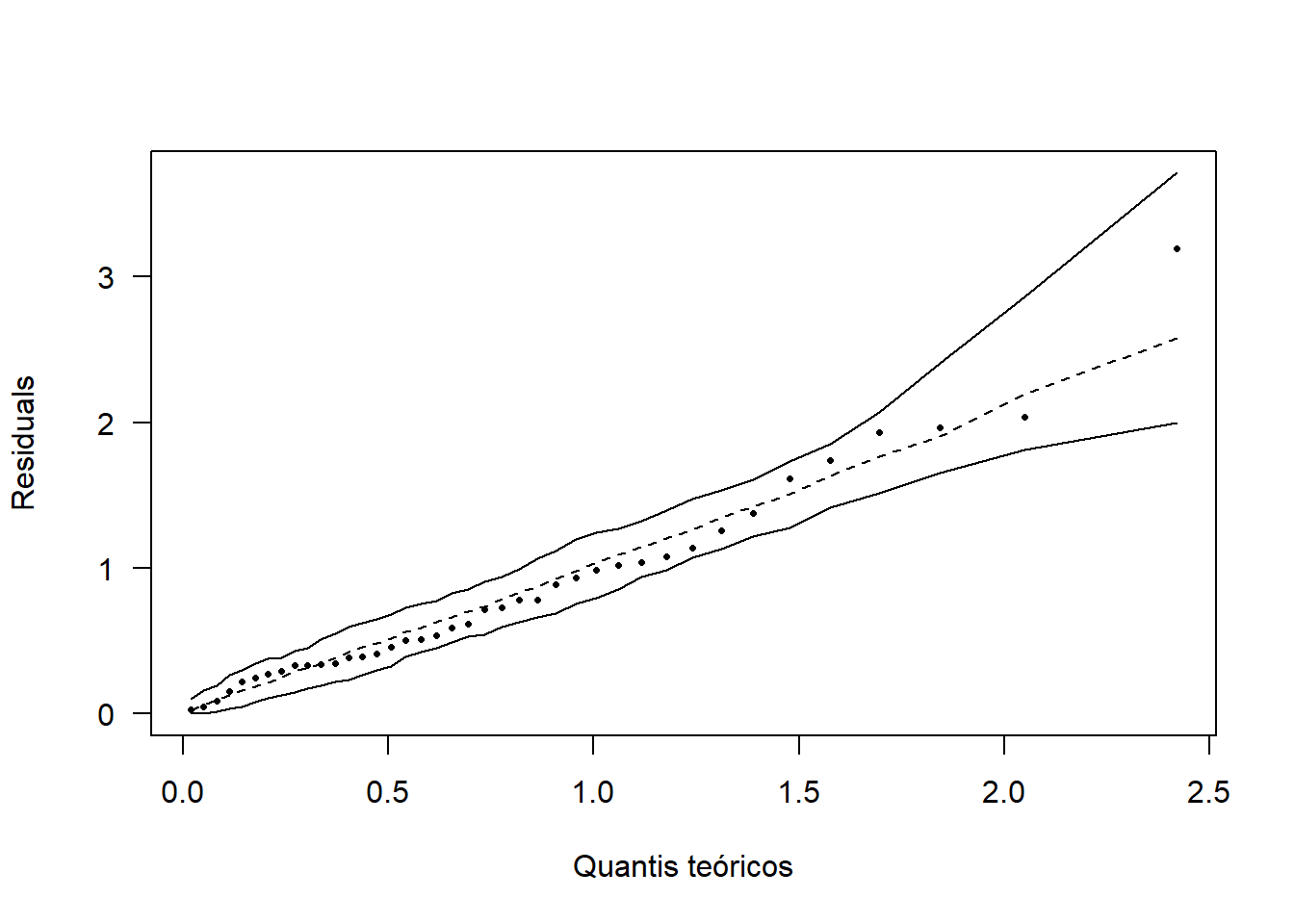
16.12.2 Homogeneidade de variâncias
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{ As variâncias são homogêneas}\\[.2cm] H_1: & \mbox{ As variâncias não são homogêneas}. \end{array} \right. \end{eqnarray*}\]
16.12.2.1 Para Fator 1
with(dados, bartlett.test(mod$residuals~F1))##
## Bartlett test of homogeneity of variances
##
## data: mod$residuals by F1
## Bartlett's K-squared = 1.1346, df = 1, p-value = 0.286816.12.2.2 Para Fator 2
with(dados, bartlett.test(mod$residuals~F2))##
## Bartlett test of homogeneity of variances
##
## data: mod$residuals by F2
## Bartlett's K-squared = 8.1367, df = 3, p-value = 0.0432716.12.2.3 Juntandos os fatores
tratamentos=rep(c(paste("T",1:8)),e=5)
with(dados, bartlett.test(mod$residuals~tratamentos))##
## Bartlett test of homogeneity of variances
##
## data: mod$residuals by tratamentos
## Bartlett's K-squared = 9.8754, df = 7, p-value = 0.195716.12.3 Independência dos erros
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: \mbox{Os erros são independentes}\\[.2cm] H_1: \mbox{Os erros não são independentes}. \end{array} \right. \end{eqnarray*}\]
(ind=lmtest::dwtest(mod))##
## Durbin-Watson test
##
## data: mod
## DW = 1.9256, p-value = 0.07498
## alternative hypothesis: true autocorrelation is greater than 0plot(mod$res, las=1, pch=19, col='red', ylab='Resíduos brutos')
abline(h=0)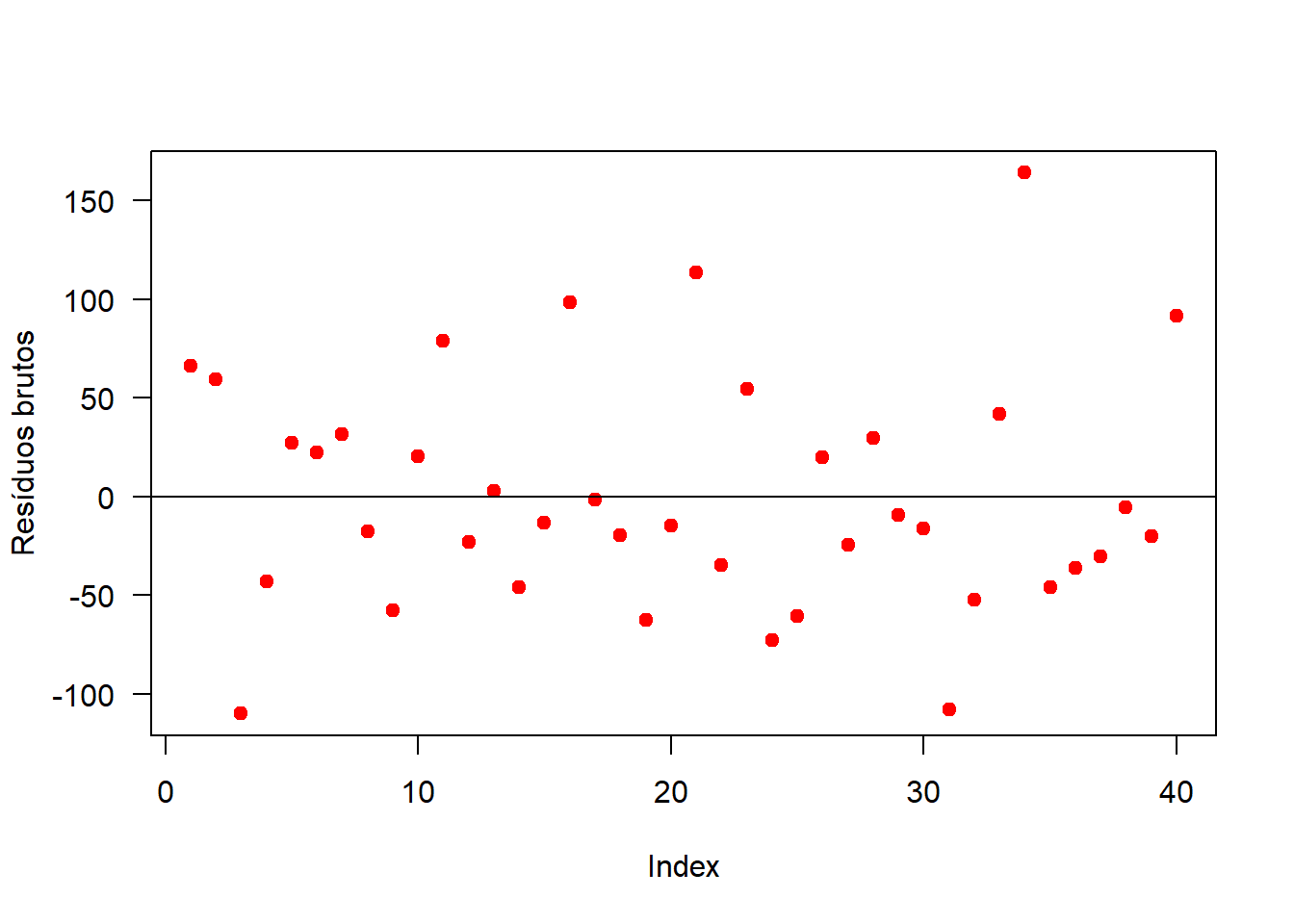
16.13 Teste de comparações
library(ExpDes.pt)
with(dados,fat2.dic(F1,F2,resp, mcomp="tukey"))## ------------------------------------------------------------------------
## Legenda:
## FATOR 1: F1
## FATOR 2: F2
## ------------------------------------------------------------------------
##
##
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr>Fc
## F1 1 11696 11696 2.7579 0.106542
## F2 3 84754 28251 6.6615 0.001272
## F1*F2 3 212960 70987 16.7382 0.000001
## Residuo 32 135712 4241
## Total 39 445123
## ------------------------------------------------------------------------
## CV = 38.68 %
##
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos (Shapiro-Wilk)
## valor-p: 0.3125183
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
##
##
##
## Interacao significativa: desdobrando a interacao
## ------------------------------------------------------------------------
##
## Desdobrando F1 dentro de cada nivel de F2
## ------------------------------------------------------------------------
## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr.Fc
## F2 3 84754.5 28251.50 6.6615 0.0013
## F1:F2 Plantio 1 26112.1 26112.10 6.1571 0.0185
## F1:F2 R1+15 1 70896.4 70896.40 16.7169 0.0003
## F1:F2 V1+15 1 15288.1 15288.10 3.6048 0.0667
## F1:F2 V3+15 1 112360.0 112360.00 26.4938 0.0000
## Residuo 32 135712.0 4241.00 NA NA
## Total 39 445123.1 11413.41 NA NA
## ------------------------------------------------------------------------
##
##
##
## F1 dentro do nivel Plantio de F2
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 1 272.8
## b 2 170.6
## ------------------------------------------------------------------------
##
##
## F1 dentro do nivel R1+15 de F2
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 1 236.6
## b 2 68.2
## ------------------------------------------------------------------------
##
##
## F1 dentro do nivel V1+15 de F2
##
## De acordo com o teste F, as medias desse fator sao estatisticamente iguais.
## ------------------------------------------------------------------------
## Niveis Medias
## 1 1 140.4
## 2 2 62.2
## ------------------------------------------------------------------------
##
##
## F1 dentro do nivel V3+15 de F2
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 2 304
## b 1 92
## ------------------------------------------------------------------------
##
##
##
## Desdobrando F2 dentro de cada nivel de F1
## ------------------------------------------------------------------------
## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr.Fc
## F1 1 11696.4 11696.40 2.7579 0.1065
## F2:F1 IN 3 105043.8 35014.58 8.2562 0.0003
## F2:F1 NI 3 192671.0 64223.65 15.1435 0.0000
## Residuo 32 135712.0 4241.00 NA NA
## Total 39 445123.1 11413.41 NA NA
## ------------------------------------------------------------------------
##
##
##
## F2 dentro do nivel IN de F1
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 1 272.8
## ab 2 236.6
## bc 3 140.4
## c 4 92
## ------------------------------------------------------------------------
##
##
## F2 dentro do nivel NI de F1
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 4 304
## b 1 170.6
## b 2 68.2
## b 3 62.2
## ------------------------------------------------------------------------16.14 Exemplo 2 (Fatorial duplo em DBC)
Supondo o mesmo exemplo anterior. Todavia, iremos considerar que o experimento foi conduzido em delineamento em blocos casualizados com cinco repetições.
NN=c(339,332,163,230,300,163,172,123,083,161,171,069,095,046,079,335,235,217,174,222,284,136,225,098,110,082,038,092,053,046,
196,252,346,468,258,032,038,063,048,160)
(Inoculacao=rep(c("IN","NI"),e=20))## [1] "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN" "IN"
## [16] "IN" "IN" "IN" "IN" "IN" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI"
## [31] "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI" "NI"(epoca=rep(c("Plantio","V1+15","V3+15","R1+15"),e=5,2))## [1] "Plantio" "Plantio" "Plantio" "Plantio" "Plantio" "V1+15" "V1+15"
## [8] "V1+15" "V1+15" "V1+15" "V3+15" "V3+15" "V3+15" "V3+15"
## [15] "V3+15" "R1+15" "R1+15" "R1+15" "R1+15" "R1+15" "Plantio"
## [22] "Plantio" "Plantio" "Plantio" "Plantio" "V1+15" "V1+15" "V1+15"
## [29] "V1+15" "V1+15" "V3+15" "V3+15" "V3+15" "V3+15" "V3+15"
## [36] "R1+15" "R1+15" "R1+15" "R1+15" "R1+15"(bloco=rep(paste("B",1:5),8))## [1] "B 1" "B 2" "B 3" "B 4" "B 5" "B 1" "B 2" "B 3" "B 4" "B 5" "B 1" "B 2"
## [13] "B 3" "B 4" "B 5" "B 1" "B 2" "B 3" "B 4" "B 5" "B 1" "B 2" "B 3" "B 4"
## [25] "B 5" "B 1" "B 2" "B 3" "B 4" "B 5" "B 1" "B 2" "B 3" "B 4" "B 5" "B 1"
## [37] "B 2" "B 3" "B 4" "B 5"F1=as.factor(Inoculacao)
F2=as.factor(epoca)
bloco=as.factor(bloco)
Trat=paste(F1,F2)
dados=data.frame(F1,F2,bloco,resp=NN)
attach(dados)
X="";Y="Número de nódulos"16.15 Estatística descritiva
Media = with(dados, mean(resp))
Variancia = with(dados, var(resp))
Desvio = with(dados, sd(resp))
CV = Desvio / Media * 100
desc = cbind(Media, Variancia, Desvio, CV)
desc| Media | Variancia | Desvio | CV |
|---|---|---|---|
| 168.35 | 11413.41 | 106.83 | 63.46 |
16.15.1 Por Inoculação
MediaA = with(dados, tapply(resp, F1, mean))
VarianciaA = with(dados, tapply(resp, F1, var))
DesvioA = with(dados, tapply(resp, F1, sd))
CVA = DesvioA / MediaA * 100
Desc = cbind(MediaA, VarianciaA, DesvioA, CVA)
Desc| MediaA | VarianciaA | DesvioA | CVA | |
|---|---|---|---|---|
| IN | 185.45 | 8229.21 | 90.71 | 48.92 |
| NI | 151.25 | 14582.72 | 120.76 | 79.84 |
16.15.2 Por época de aplicação
MediaB = with(dados, tapply(resp, F2, mean))
VarianciaB = with(dados, tapply(resp, F2, var))
DesvioB = with(dados, tapply(resp, F2, sd))
CVB = DesvioB / MediaB * 100
Desc = cbind(MediaB, VarianciaB, DesvioB, CVB)
Desc| MediaB | VarianciaB | DesvioB | CVB | |
|---|---|---|---|---|
| Plantio | 221.7 | 8287.34 | 91.03 | 41.06 |
| R1+15 | 152.4 | 10686.93 | 103.38 | 67.83 |
| V1+15 | 101.3 | 2559.12 | 50.59 | 49.94 |
| V3+15 | 198.0 | 18507.56 | 136.04 | 68.71 |
16.16 Gráficos exploratórios
16.16.1 Gráfico de Caixas
16.16.1.1 Fator 1
par(bty='l', mai=c(1, 1, .2, .2))
par(cex=0.7)
caixas=with(dados, car::Boxplot(resp ~ F1, vertical=T,las=1, col='Lightyellow',
xlab=X, ylab=Y))
mediab=with(dados,tapply(resp, F1, mean))
points(mediab, pch='+', cex=1.5, col='red')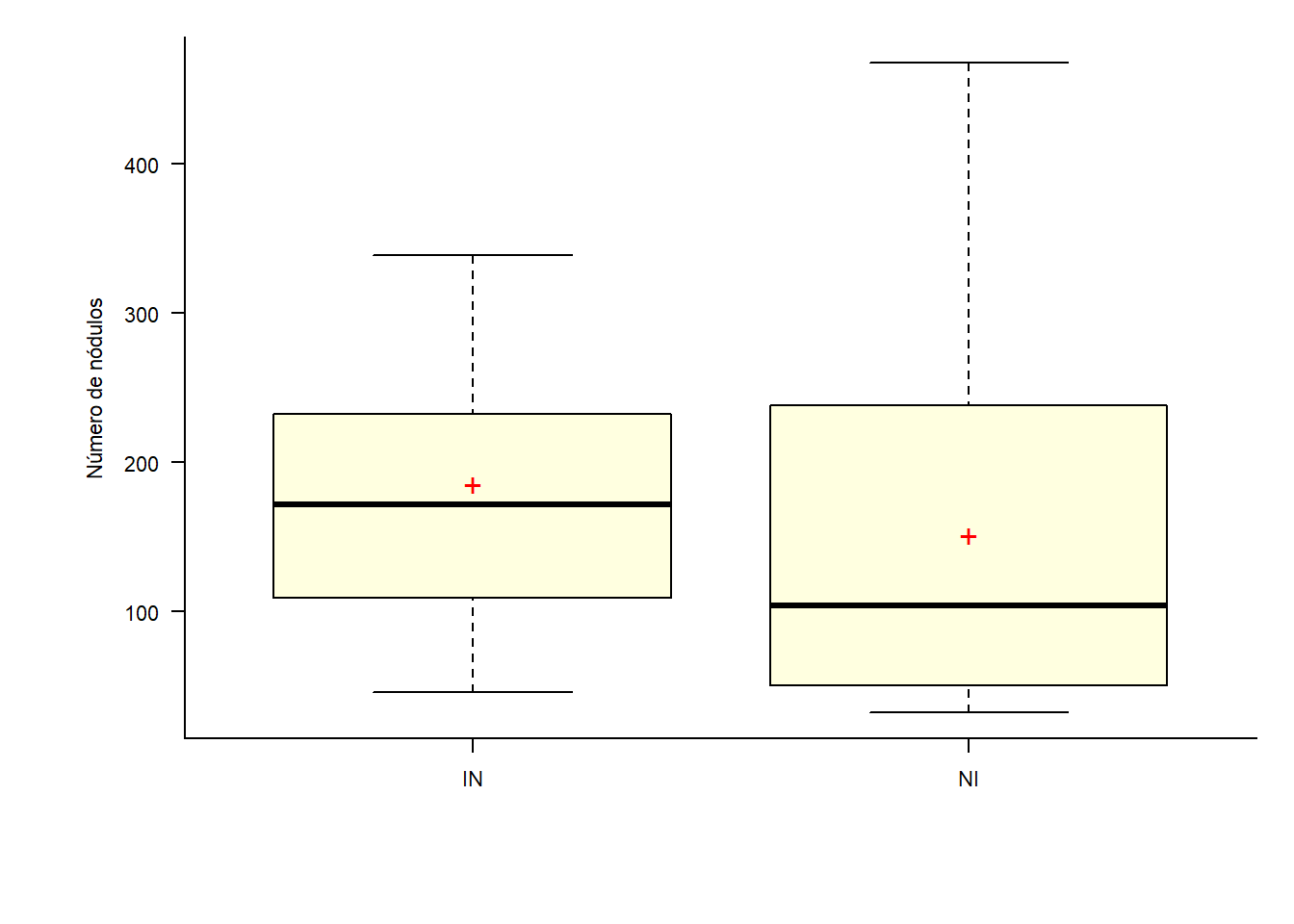
16.16.1.2 Fator 2
par(bty='l', mai=c(1, 1, .2, .2))
par(cex=0.7)
caixas=with(dados, car::Boxplot(resp ~ F2, vertical=T,las=1, col='Lightyellow',
xlab=X, ylab=Y))
mediab=with(dados,tapply(resp, F2, mean))
points(mediab, pch='+', cex=1.5, col='red')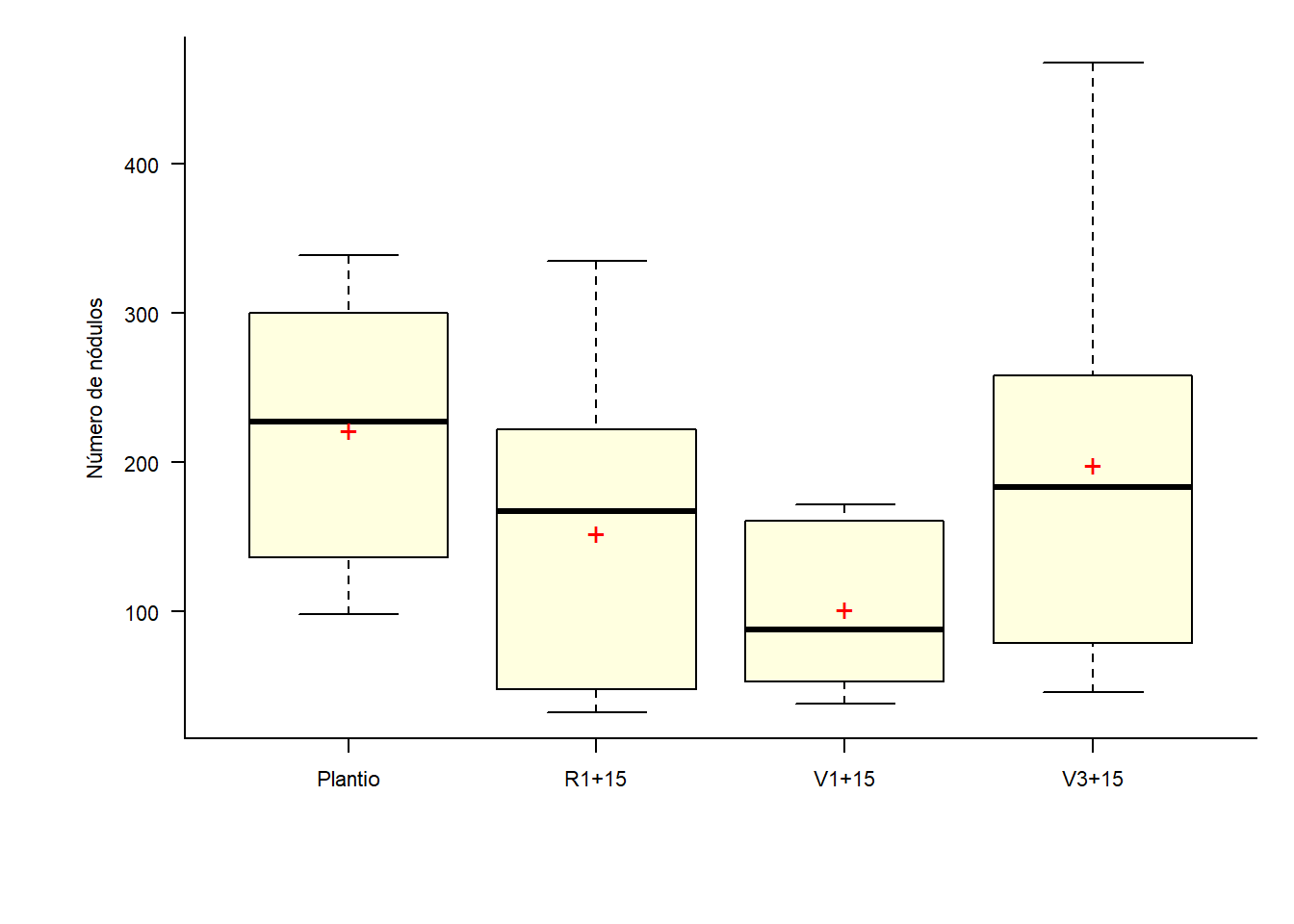
16.16.1.3 Juntando Fatores
par(bty='l', mai=c(1, 1, .2, .2))
par(cex=0.7)
caixas=with(dados, car::Boxplot(resp ~ F1*F2, vertical=T,las=1, col='Lightyellow',
xlab=X, ylab=Y))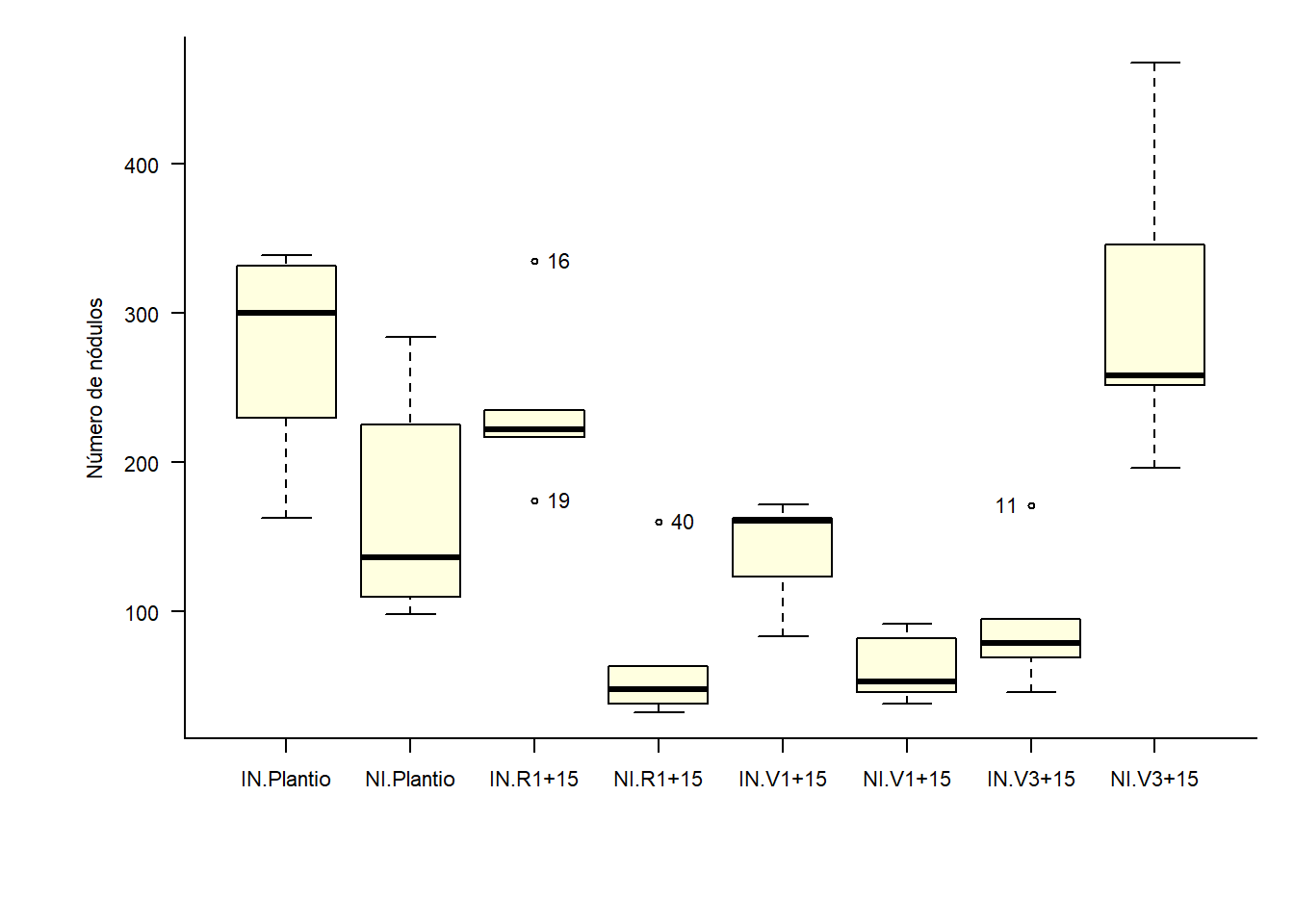
16.16.2 Gráfico de interação
with(dados, interaction.plot(F2, F1, resp, las=1, col=1:6, bty='l',
xlab='', ylab='CBM', trace.label="FATOR1"))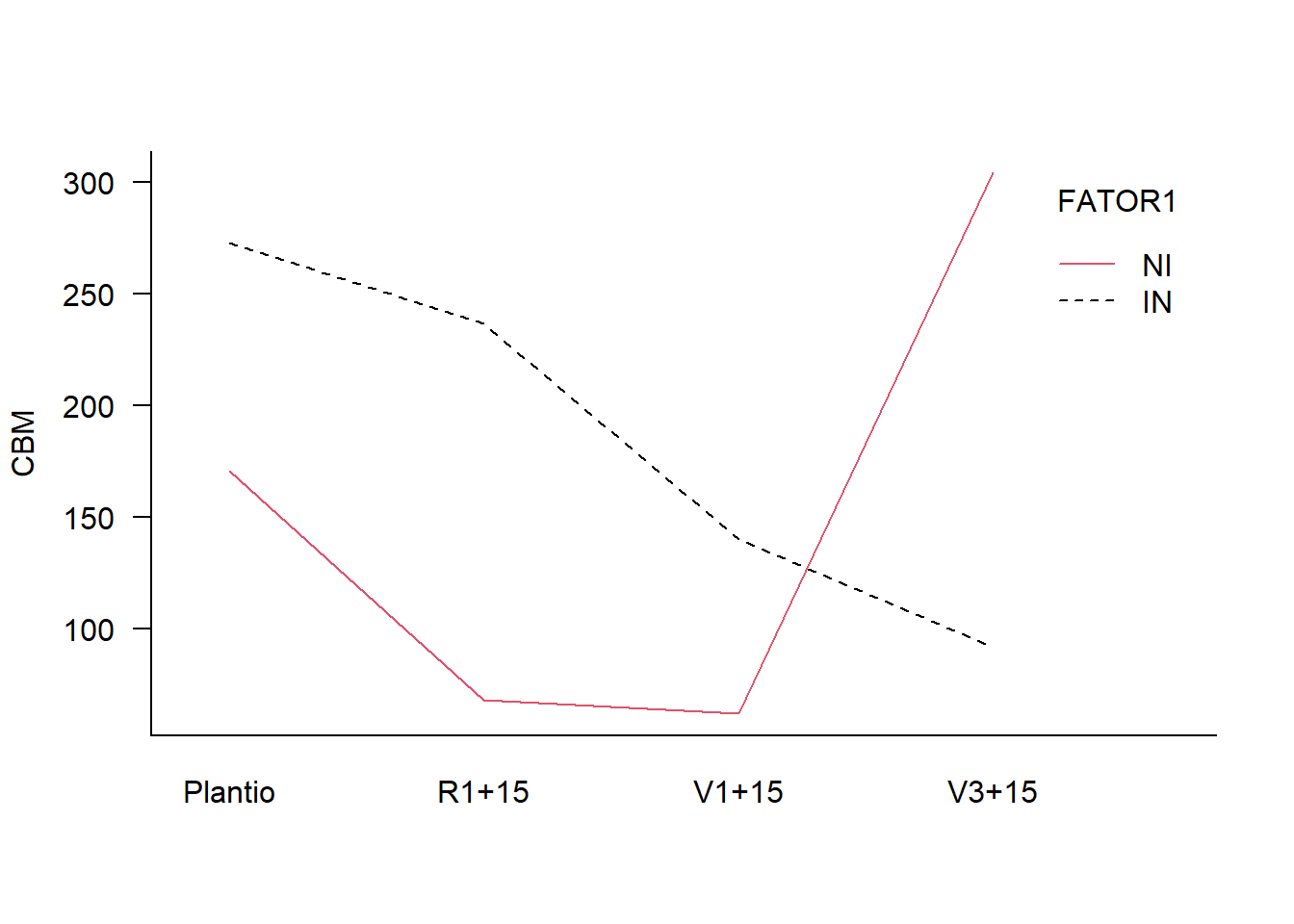
# FATOR1 e FATOR2
with(dados, interaction.plot(F1, F2, resp, las=1, col=1:6, bty='l',
xlab='', ylab='CBM', trace.label="FATOR2"))
16.17 Análise de Variância
Hipótese do Fator 1:
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2\\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
Hipótese do Fator 2:
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 = \mu_3 = \mu_4 \\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
Hipótese da interação:
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{Todas as combinações entre os níveis do fator 1 e do fator 2 têm o mesmo efeito} \\[.2cm] H_1: & \mbox{Pelo menos duas combinações entre os níveis do fator 1 e do fator 2 têm efeitos diferentes}. \end{array} \right. \end{eqnarray*}\]
mod = with(dados, aov(resp~F1*F2+bloco))
anova(mod)| GL | SQ | QM | Teste F | p-valor | |
|---|---|---|---|---|---|
| F1 | 1 | 11696.4 | 11696.400 | 2.6390284 | 0.1154728 |
| F2 | 3 | 84754.5 | 28251.500 | 6.3743126 | 0.0019764 |
| bloco | 4 | 11613.6 | 2903.400 | 0.6550866 | 0.6282168 |
| F1:F2 | 3 | 212960.2 | 70986.733 | 16.0165525 | 0.0000030 |
| Residuals | 28 | 124098.4 | 4432.086 |
16.18 Pressuposições
16.18.1 Normalidade dos erros
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{Os erros seguem distribuição normal}\\[.2cm] H_1: & \mbox{Os erros não seguem distribuição normal}. \end{array} \right. \end{eqnarray*}\]
(norm=shapiro.test(mod$res))##
## Shapiro-Wilk normality test
##
## data: mod$res
## W = 0.95489, p-value = 0.1118hnp::hnp(mod, las=1, xlab="Quantis teóricos", pch=16)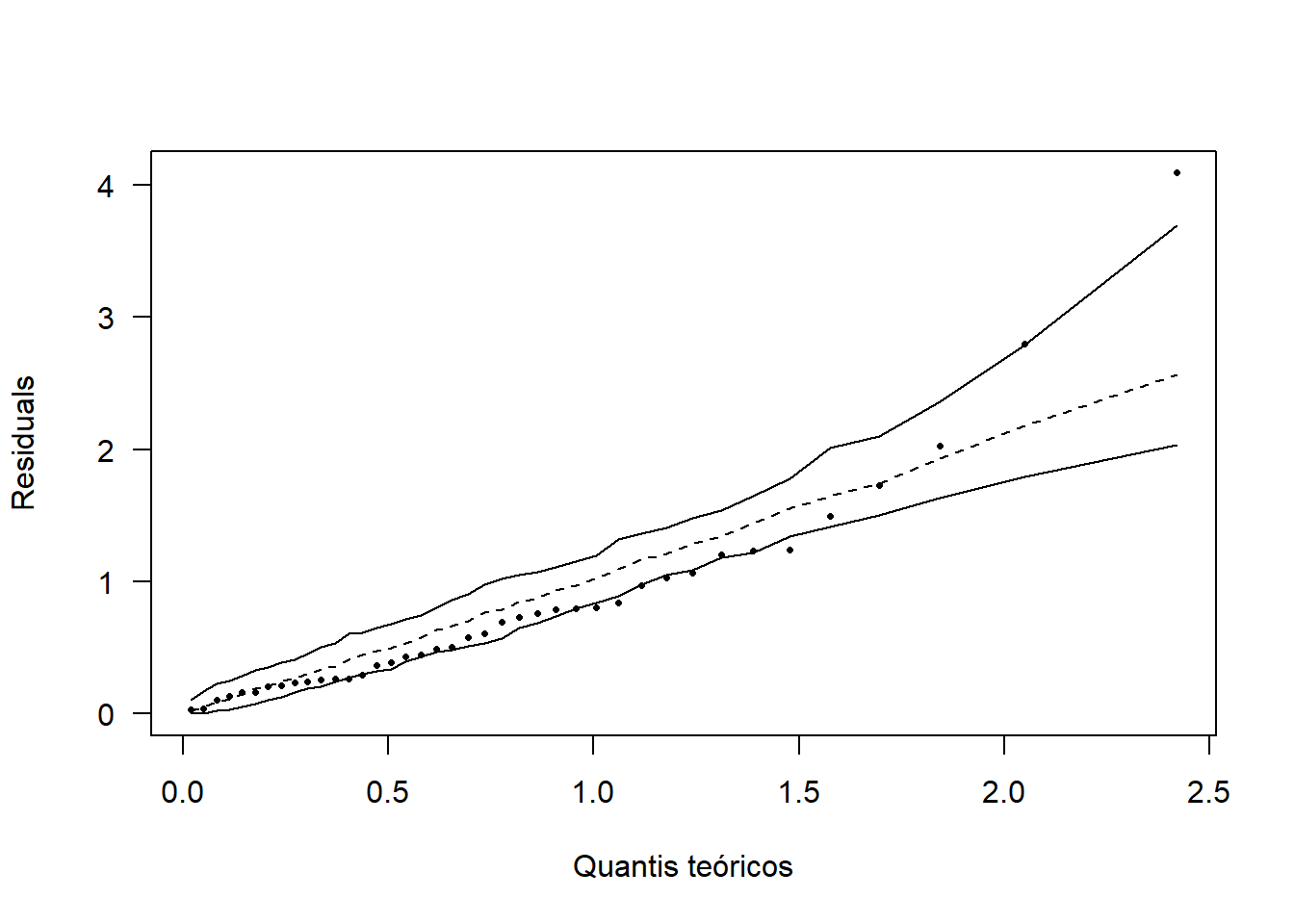
16.18.2 Homogeneidade de variâncias
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mbox{ As variâncias são homogêneas}\\[.2cm] H_1: & \mbox{ As variâncias não são homogêneas}. \end{array} \right. \end{eqnarray*}\]
16.18.2.1 Para Fator 1
with(dados, bartlett.test(mod$residuals~F1))##
## Bartlett test of homogeneity of variances
##
## data: mod$residuals by F1
## Bartlett's K-squared = 4.6002, df = 1, p-value = 0.0319716.18.2.2 Para Fator 2
with(dados, bartlett.test(mod$residuals~F2))##
## Bartlett test of homogeneity of variances
##
## data: mod$residuals by F2
## Bartlett's K-squared = 10.875, df = 3, p-value = 0.0124216.18.2.3 Juntandos os fatores
tratamentos=rep(c(paste("T",1:8)),e=5)
with(dados, bartlett.test(mod$residuals~tratamentos))##
## Bartlett test of homogeneity of variances
##
## data: mod$residuals by tratamentos
## Bartlett's K-squared = 16.111, df = 7, p-value = 0.0241216.18.3 Independência dos erros
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: \mbox{Os erros são independentes}\\[.2cm] H_1: \mbox{Os erros não são independentes}. \end{array} \right. \end{eqnarray*}\]
(ind=lmtest::dwtest(mod))##
## Durbin-Watson test
##
## data: mod
## DW = 1.8654, p-value = 0.06734
## alternative hypothesis: true autocorrelation is greater than 0plot(mod$res, las=1, pch=19, col='red', ylab='Resíduos brutos')
abline(h=0)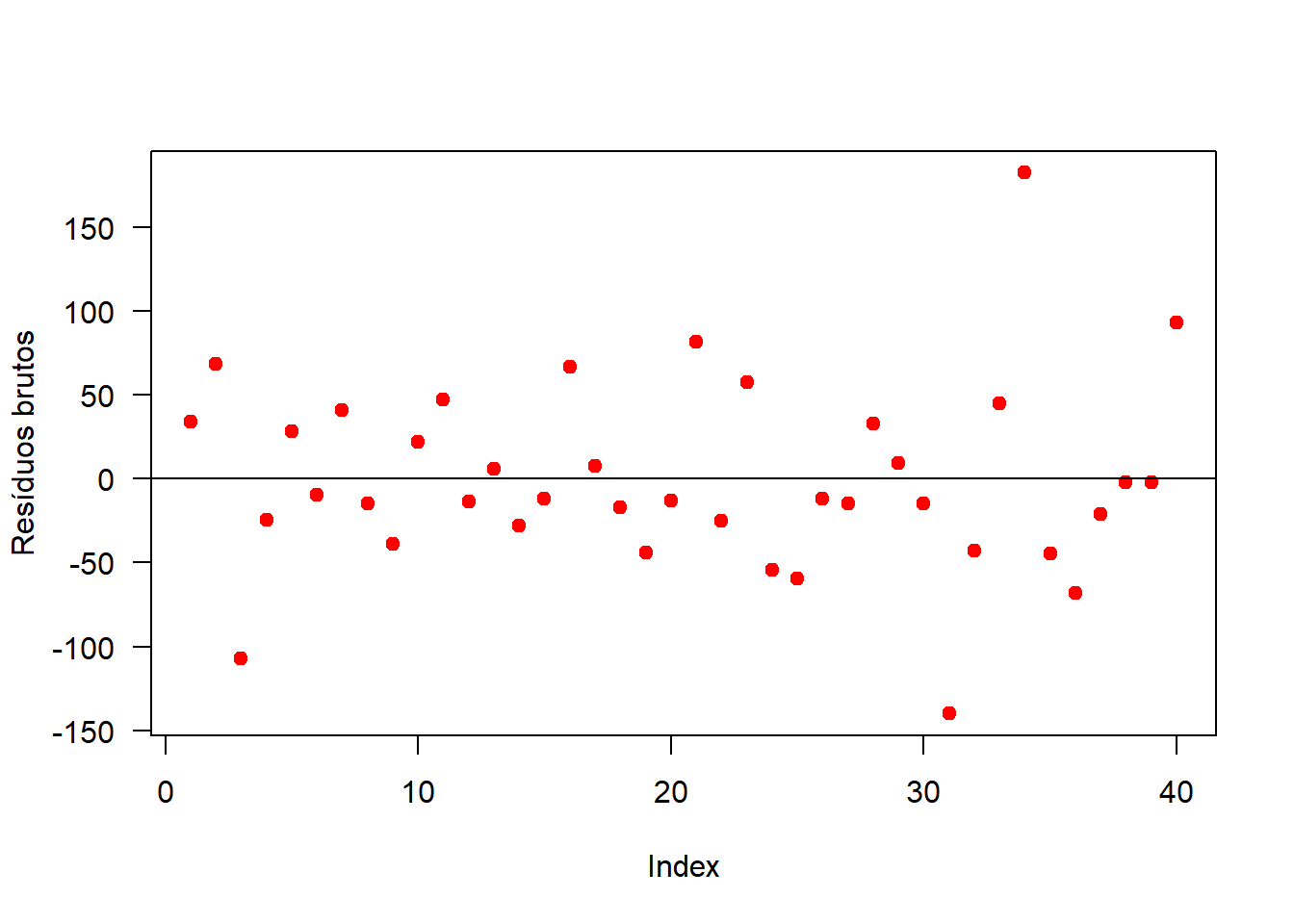
16.19 Teste de comparações
library(ExpDes.pt)
with(dados,fat2.dbc(F1,F2,bloco,resp, mcomp="tukey"))## ------------------------------------------------------------------------
## Legenda:
## FATOR 1: F1
## FATOR 2: F2
## ------------------------------------------------------------------------
##
##
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr>Fc
## Bloco 4 11614 2903 0.6551 0.62822
## F1 1 11696 11696 2.6390 0.11547
## F2 3 84755 28252 6.3743 0.00198
## F1*F2 3 212960 70987 16.0166 0.00000
## Residuo 28 124098 4432
## Total 39 445123
## ------------------------------------------------------------------------
## CV = 39.54 %
##
## ------------------------------------------------------------------------
## Teste de normalidade dos residuos (Shapiro-Wilk)
## valor-p: 0.1117923
## De acordo com o teste de Shapiro-Wilk a 5% de significancia, os residuos podem ser considerados normais.
## ------------------------------------------------------------------------
##
##
##
## Interacao significativa: desdobrando a interacao
## ------------------------------------------------------------------------
##
## Desdobrando F1 dentro de cada nivel de F2
## ------------------------------------------------------------------------
## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr.Fc
## Bloco 4 11613.6 2903.400 0.6551 0.6282
## F2 3 84754.5 28251.500 6.3743 0.0020
## F1:F2 Plantio 1 26112.1 26112.100 5.8916 0.0219
## F1:F2 R1+15 1 70896.4 70896.400 15.9962 0.0004
## F1:F2 V1+15 1 15288.1 15288.100 3.4494 0.0738
## F1:F2 V3+15 1 112360.0 112360.000 25.3515 0.0000
## Residuo 28 124098.4 4432.086 NA
## Total 39 445123.1 11413.413 NA
## ------------------------------------------------------------------------
##
##
##
## F1 dentro do nivel Plantio de F2
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 1 272.8
## b 2 170.6
## ------------------------------------------------------------------------
##
##
## F1 dentro do nivel R1+15 de F2
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 1 236.6
## b 2 68.2
## ------------------------------------------------------------------------
##
##
## F1 dentro do nivel V1+15 de F2
##
## De acordo com o teste F, as medias desse fator sao estatisticamente iguais.
## ------------------------------------------------------------------------
## Niveis Medias
## 1 1 140.4
## 2 2 62.2
## ------------------------------------------------------------------------
##
##
## F1 dentro do nivel V3+15 de F2
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 2 304
## b 1 92
## ------------------------------------------------------------------------
##
##
##
## Desdobrando F2 dentro de cada nivel de F1
## ------------------------------------------------------------------------
## ------------------------------------------------------------------------
## Quadro da analise de variancia
## ------------------------------------------------------------------------
## GL SQ QM Fc Pr.Fc
## Bloco 4 11613.6 2903.400 0.6551 0.6282
## F1 1 11696.4 11696.400 2.639 0.1155
## F2:F1 IN 3 105043.8 35014.583 7.9002 0.0006
## F2:F1 NI 3 192671.0 64223.650 14.4906 0.0000
## Residuo 28 124098.4 4432.086 NA
## Total 39 445123.1 11413.413 NA
## ------------------------------------------------------------------------
##
##
##
## F2 dentro do nivel IN de F1
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 1 272.8
## ab 2 236.6
## bc 3 140.4
## c 4 92
## ------------------------------------------------------------------------
##
##
## F2 dentro do nivel NI de F1
## ------------------------------------------------------------------------
## Teste de Tukey
## ------------------------------------------------------------------------
## Grupos Tratamentos Medias
## a 4 304
## b 1 170.6
## b 2 68.2
## b 3 62.2
## ------------------------------------------------------------------------# ou
library(easyanova)
ea2(dados, design = 2)
## $`Analysis of variance`
## df type III SS mean square F value p>F
## factor_1 1 11696.4 11696.400 2.639 0.1155
## factor_2 3 84754.5 28251.500 6.3743 0.002
## blocks 4 11613.6 2903.400 0.6551 0.6282
## factor_1:factor_2 3 212960.2 70986.733 16.0166 <0.001
## residuals 28 124098.4 4432.086 - -
##
## $`Adjusted means (factor 1)`
## factor_1 adjusted.mean standard.error tukey snk duncan t scott_knott
## 1 IN 185.45 14.8864 a a a a a
## 2 NI 151.25 14.8864 a a a a a
##
## $`Multiple comparison test (factor 1)`
## pair contrast p(tukey) p(snk) p(duncan) p(t)
## 1 IN - NI 34.2 0.1155 0.1155 0.1155 0.1155
##
## $`Adjusted means (factor 2)`
## factor_2 adjusted.mean standard.error tukey snk duncan t scott_knott
## 1 Plantio 221.7 21.0525 a a a a a
## 2 V3+15 198.0 21.0525 a a ab ab a
## 3 R1+15 152.4 21.0525 ab ab bc bc b
## 4 V1+15 101.3 21.0525 b b c c b
##
## $`Multiple comparison test (factor 2)`
## pair contrast p(tukey) p(snk) p(duncan) p(t)
## 1 Plantio - V3+15 23.7 0.8556 0.4327 0.4327 0.4327
## 2 Plantio - R1+15 69.3 0.1158 0.0683 0.0347 0.0274
## 3 Plantio - V1+15 120.4 0.0020 0.0020 0.0007 0.0004
## 4 V3+15 - R1+15 45.6 0.4329 0.1368 0.1368 0.1368
## 5 V3+15 - V1+15 96.7 0.0151 0.0082 0.0041 0.0030
## 6 R1+15 - V1+15 51.1 0.3344 0.0971 0.0971 0.0971
##
## $`Adjusted means (factor 1 in levels of factor 2)`
## $`Adjusted means (factor 1 in levels of factor 2)`$`factor_1 in Plantio`
## treatment adjusted.mean standard.error tukey snk duncan t scott_knott
## 1 IN.Plantio 272.8 29.7728 a a a a a
## 2 NI.Plantio 170.6 29.7728 b b b b b
##
## $`Adjusted means (factor 1 in levels of factor 2)`$`factor_1 in R1+15`
## treatment adjusted.mean standard.error tukey snk duncan t scott_knott
## 3 IN.R1+15 236.6 29.7728 a a a a a
## 4 NI.R1+15 68.2 29.7728 b b b b b
##
## $`Adjusted means (factor 1 in levels of factor 2)`$`factor_1 in V1+15`
## treatment adjusted.mean standard.error tukey snk duncan t scott_knott
## 5 IN.V1+15 140.4 29.7728 a a a a a
## 6 NI.V1+15 62.2 29.7728 a a a a a
##
## $`Adjusted means (factor 1 in levels of factor 2)`$`factor_1 in V3+15`
## treatment adjusted.mean standard.error tukey snk duncan t scott_knott
## 8 NI.V3+15 304 29.7728 a a a a a
## 7 IN.V3+15 92 29.7728 b b b b b
##
##
## $`Multiple comparison test (factor 1 in levels of factor 2)`
## $`Multiple comparison test (factor 1 in levels of factor 2)`$`factor_1 in Plantio`
## pair contrast p(tukey) p(snk) p(duncan) p(t)
## 1 IN.Plantio - NI.Plantio 102.2 0.0219 0.0219 0.0219 0.0219
##
## $`Multiple comparison test (factor 1 in levels of factor 2)`$`factor_1 in R1+15`
## pair contrast p(tukey) p(snk) p(duncan) p(t)
## 1 IN.R1+15 - NI.R1+15 168.4 4e-04 4e-04 4e-04 4e-04
##
## $`Multiple comparison test (factor 1 in levels of factor 2)`$`factor_1 in V1+15`
## pair contrast p(tukey) p(snk) p(duncan) p(t)
## 1 IN.V1+15 - NI.V1+15 78.2 0.0738 0.0738 0.0738 0.0738
##
## $`Multiple comparison test (factor 1 in levels of factor 2)`$`factor_1 in V3+15`
## pair contrast p(tukey) p(snk) p(duncan) p(t)
## 1 NI.V3+15 - IN.V3+15 212 0 0 0 0
##
##
## $`Adjusted means (factor 2 in levels of factor 1)`
## $`Adjusted means (factor 2 in levels of factor 1)`$`factor_2 in IN`
## treatment adjusted.mean standard.error tukey snk duncan t scott_knott
## 1 IN.Plantio 272.8 29.7728 a a a a a
## 3 IN.R1+15 236.6 29.7728 ab a a a a
## 5 IN.V1+15 140.4 29.7728 bc b b b b
## 7 IN.V3+15 92.0 29.7728 c b b b b
##
## $`Adjusted means (factor 2 in levels of factor 1)`$`factor_2 in NI`
## treatment adjusted.mean standard.error tukey snk duncan t scott_knott
## 8 NI.V3+15 304.0 29.7728 a a a a a
## 2 NI.Plantio 170.6 29.7728 b b b b b
## 4 NI.R1+15 68.2 29.7728 b c c c c
## 6 NI.V1+15 62.2 29.7728 b c c c c
##
##
## $`Multiple comparison test (factor 2 in levels of factor 1)`
## $`Multiple comparison test (factor 2 in levels of factor 1)`$`factor_2 in IN`
## pair contrast p(tukey) p(snk) p(duncan) p(t)
## 1 IN.Plantio - IN.R1+15 36.2 0.8253 0.3972 0.3972 0.3972
## 2 IN.Plantio - IN.V1+15 132.4 0.0193 0.0106 0.0053 0.0039
## 3 IN.Plantio - IN.V3+15 180.8 0.0010 0.0010 0.0003 0.0002
## 4 IN.R1+15 - IN.V1+15 96.2 0.1259 0.0301 0.0301 0.0301
## 5 IN.R1+15 - IN.V3+15 144.6 0.0095 0.0051 0.0026 0.0019
## 6 IN.V1+15 - IN.V3+15 48.4 0.6627 0.2601 0.2601 0.2601
##
## $`Multiple comparison test (factor 2 in levels of factor 1)`$`factor_2 in NI`
## pair contrast p(tukey) p(snk) p(duncan) p(t)
## 1 NI.V3+15 - NI.Plantio 133.4 0.0182 0.0037 0.0037 0.0037
## 2 NI.V3+15 - NI.R1+15 235.8 0.0000 0.0000 0.0000 0.0000
## 3 NI.V3+15 - NI.V1+15 241.8 0.0000 0.0000 0.0000 0.0000
## 4 NI.Plantio - NI.R1+15 102.4 0.0940 0.0217 0.0217 0.0217
## 5 NI.Plantio - NI.V1+15 108.4 0.0700 0.0402 0.0203 0.0156
## 6 NI.R1+15 - NI.V1+15 6.0 0.9989 0.8877 0.8877 0.8877
##
##
## $`Residual analysis`
## $`Residual analysis`$`residual analysis`
## values
## p.value Shapiro-Wilk test 0.1118
## p.value Bartlett test (factor_1) 0.0320
## p.value Bartlett test (factor_2) 0.0124
## p.value Bartlett test (treatments) 0.0241
## coefficient of variation (%) 39.5400
## first value most discrepant 34.0000
## second value most discrepant 31.0000
## third value most discrepant 3.0000
##
## $`Residual analysis`$residuals
## 1 2 3 4 5 6 7 8 9 10
## 34.30 68.55 -106.95 -24.45 28.55 -9.30 40.95 -14.55 -39.05 21.95
## 11 12 13 14 15 16 17 18 19 20
## 47.10 -13.65 5.85 -27.65 -11.65 66.50 7.75 -16.75 -44.25 -13.25
## 21 22 23 24 25 26 27 28 29 30
## 81.50 -25.25 57.25 -54.25 -59.25 -12.10 -14.85 32.65 9.15 -14.85
## 31 32 33 34 35 36 37 38 39 40
## -139.90 -42.65 44.85 182.35 -44.65 -68.10 -20.85 -2.35 -1.85 93.15
##
## $`Residual analysis`$`standardized residuals`
## 1 2 3 4 5 6
## 0.60805566 1.21522493 -1.89596363 -0.43343909 0.50612213 -0.16486640
## 7 8 9 10 11 12
## 0.72594400 -0.25793615 -0.69226161 0.38912016 0.83496855 -0.24198133
## 13 14 15 16 17 18
## 0.10370629 -0.49016731 -0.20652619 1.17888341 0.13738867 -0.29693680
## 19 20 21 22 23 24
## -0.78444498 -0.23489030 1.44479697 -0.44762115 1.01490339 -0.96172068
## 25 26 27 28 29 30
## -1.05035853 -0.21450360 -0.26325442 0.57880517 0.16220727 -0.26325442
## 31 32 33 34 35 36
## -2.48008706 -0.75608087 0.79508152 3.23262242 -0.79153601 -1.20724753
## 37 38 39 40
## -0.36961984 -0.04165979 -0.03279600 1.65132316