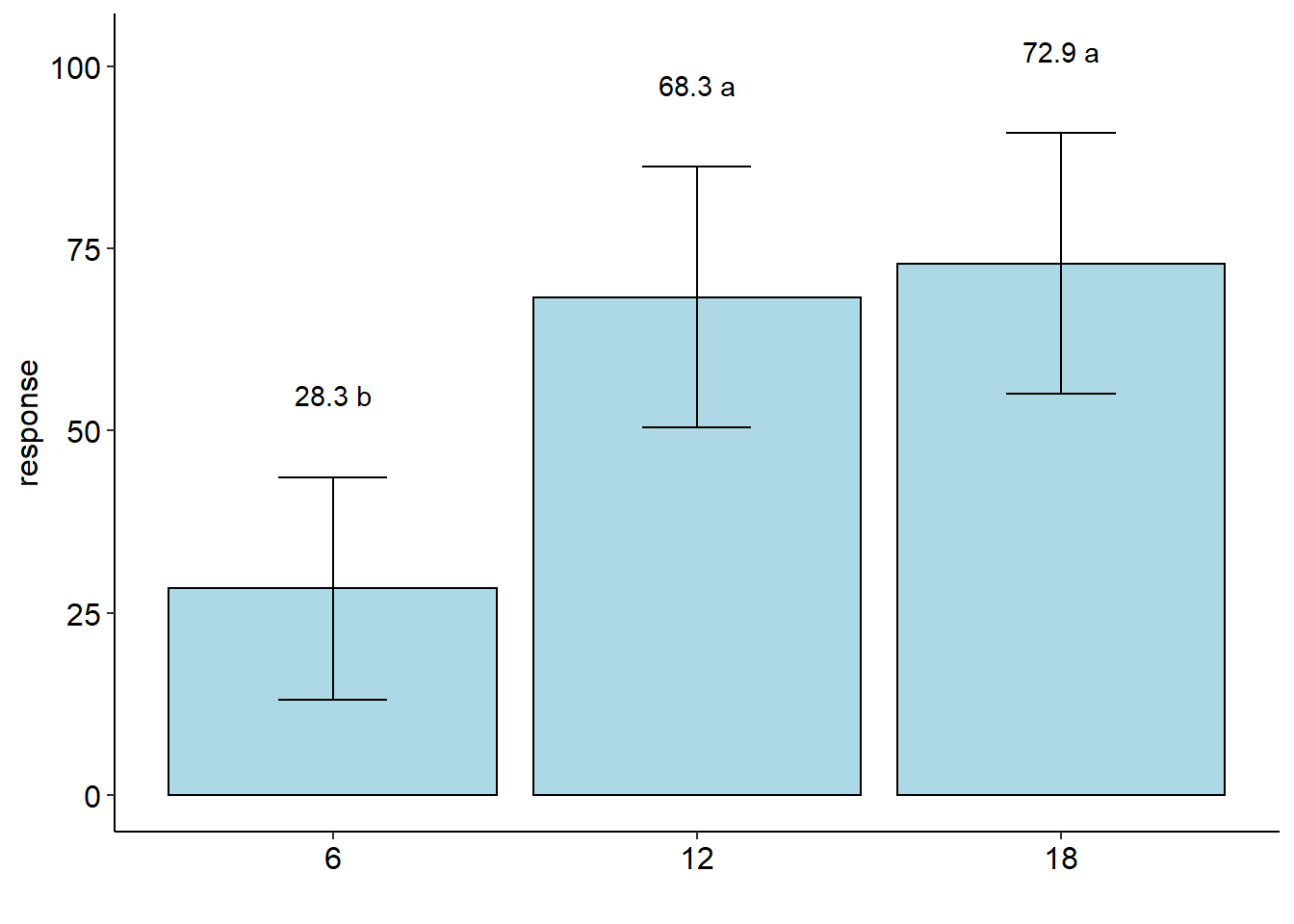14 Análise conjunta

14.1 Teoria

Na experimentação agrícola é comum a instalação de grupos de ensaios iguais, ou seja, com a mesma estrutura (delineamento, repetições e tratamentos iguais), entretanto, em anos e/ou locais distintos, visando a obtenção de conclusões mais abrangentes. Este tipo de análise é denominada análise conjunta de experimentos ou também conhecido como análise de grupos de experimentos.

Requisitos para análise de variância conjunta

Definir local (Ambiente) onde a pesquisa será conduzida, ou seja, diferentes localidades, anos diferentes de uma mesma localidade, anos e localidades distintas, etc. instalam-se os experimentos, o que geralmente são implantados em blocos casualziados, e após a coleta dos daddos, realizam-se todas às análises individuais, isto é, análise para cada ambiente de acordo com o delineamento estatístico utilizado.
Examina-se a seguir as grandezas dos \(QM_{Res}\), ou seja, se forem homogêneas (Quando a razão entre a maior e o menor \(QM_{Res}\) não for superior a mais de sete vezes) todos os ambientes poderão ser incluídos na análise conjunta sem restrições, do contrário, devem-se organizar subgrupos com QMresíduos homogêneos, sendo as análises conjuntas feitas para cada subgrupo.

FV	G.L.	S.Q.	Q.M.	Fcalc
Tratamento	\(t-1\)	\(SQ_{Tratamento}\)	\(\frac{SQ_{Tratamento}}{t-1}\)	\(\frac{QM_{trat}}{QM_{T x A}}\)
Ambientes	\(a-1\)	\(SQ_{Ambiente}\)	\(\frac{SQ_{tratamento}}{a-1}\)	\(\frac{QM_{a}}{QM_{T x A}}\)
Interação T x A	\((t-1)(a-1)\)	\(SQ_{Interação}\)	\(\frac{SQ_{T x A}}{(t-1)(a-1)}\)	\(\frac{QM_{T x A}}{QM_{res}}\)
Resíduo médio	\(N'\)	\(SQ_{res}\)	\(\frac{SQ_{res}}{N}\)
Total	\(at-1\)	\(SQ_{Total}\)

No AgroR, é possível realizar essa análise usando o comando conjdic ou conjdbc, conforme a seguir:

library(AgroR)
data(mirtilo)
with(mirtilo, conjdbc(trat, bloco, exp, resp))

## Warning in aov(resp ~ bloco + local + local:bloco + tratamento + Error(local:
## (bloco + : Error() model is singular

## 
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
##                          Method Statistic   p.value
##  Shapiro-Wilk normality test(W) 0.9812789 0.7876433
## 
## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
##                               Method Statistic   p.value
##  Bartlett test(Bartlett's K-squared)  1.094921 0.5784169
## 
## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
##                  Method Statistic   p.value
##  Durbin-Watson test(DW)  2.377661 0.4700462
## 
## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent
## -----------------------------------------------------------------
## Test Homogeneity of experiments
## -----------------------------------------------------------------
## [1] 5.481481
## 
## Based on the analysis of variance and homogeneity of experiments, it can be concluded that:

## The experiments can be analyzed together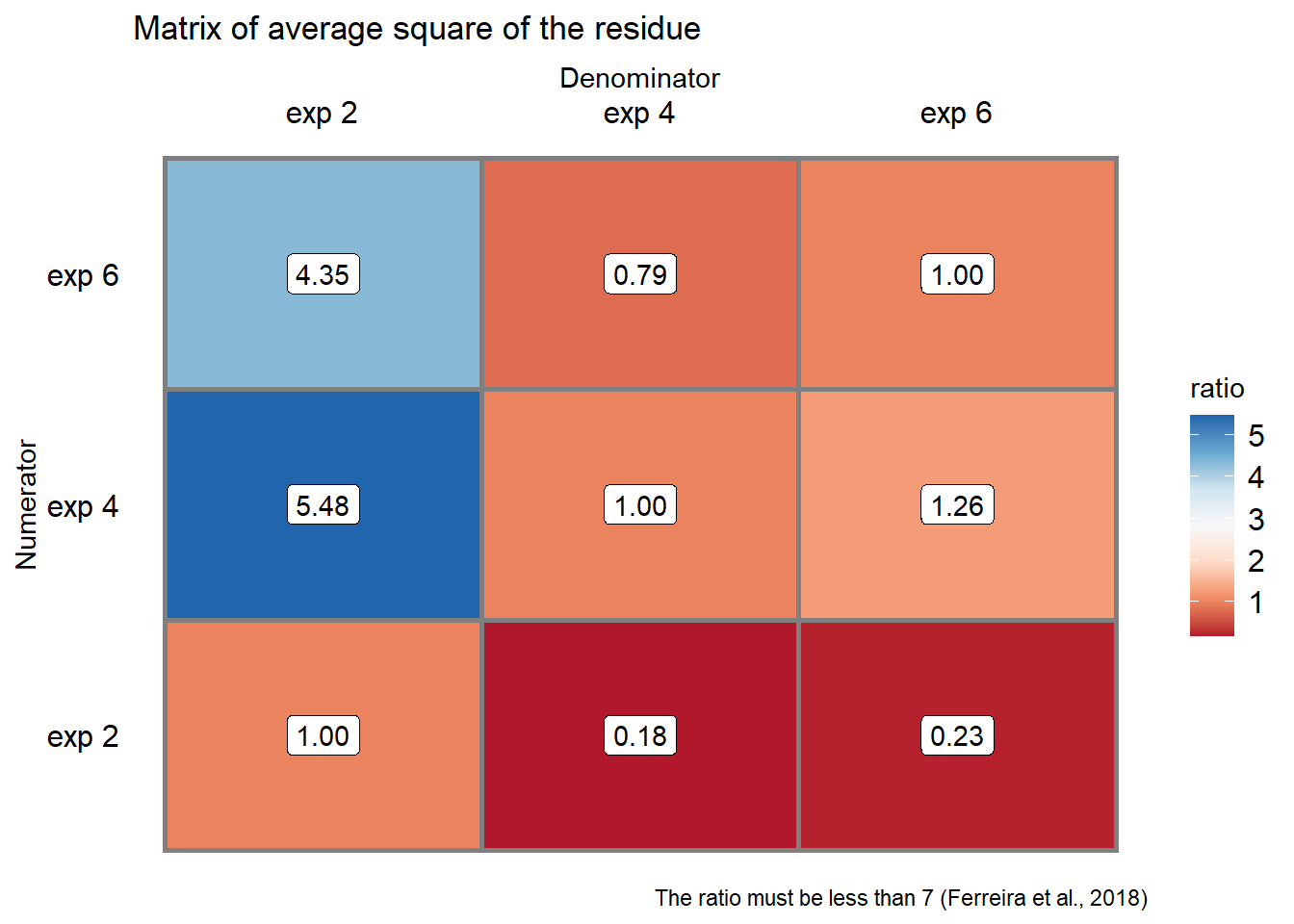

## 
## 
## 
## -----------------------------------------------------------------
## Analysis of variance
## -----------------------------------------------------------------
##                 Df     Sum Sq    Mean Sq    F value      Pr(>F)
## Trat             2 14434.7222 7217.36111 45.9867257 0.001737072
## Exp              2  4809.7222 2404.86111 15.3230088 0.013329484
## Block/Local      6   362.5000   60.41667  0.3849558 0.857661006
## Exp:Trat         4   627.7778  156.94444  0.7730901 0.556825561
## Average residue 21  4263.1944  203.00926                       
## 
## -----------------------------------------------------------------
## Multiple comparison test ( tukey )
## -----------------------------------------------------------------
##        resp groups
## 18 72.91667      a
## 12 68.33333      a
## 6  28.33333      b