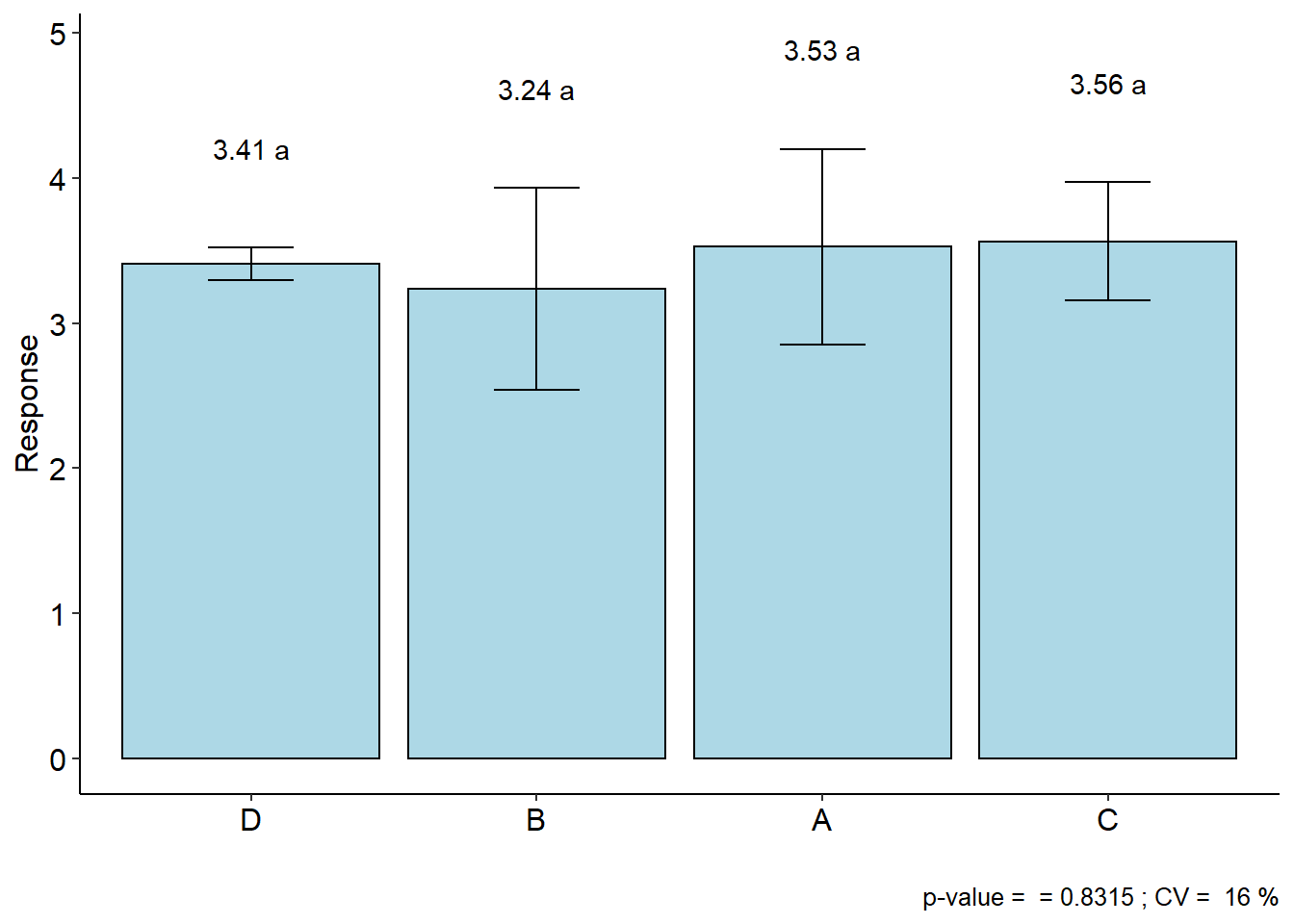8 Delineamento em quadrado latino
8.1 Teoria
- Na sessão de delineamento em blocos ao acaso, observamos que o mesmo é usado para reduzir o erro residual de um experimento utilizando o princípio do controle local;
- No Delineamento em Quadrado Latino, além dos princípios da repetição e da casualização, o princípio do controle local é utilizado duas vezes para controlar o efeito de dois fatores;
- Para controlar esta variabilidade, é necessário dividir as unidades experimentais em blocos homogêneos de unidades experimentais em relação a cada fator controlado.
- O número de blocos para cada fator controlado deve ser igual ao número de tratamentos. Uma vez formados os blocos, distribui-se os tratamentos ao acaso com a restrição que cada tratamento seja designado uma única vez em cada um dos blocos dos dois fatores controlados.
- Os níveis de um fator controlado são identificados por linhas em uma tabela de dupla entrada e os níveis do outro fator controlado são identificados por colunas na tabela.
- A grande restrição dos ensaios em quadrados latinos é que para 2, 3 ou 4 tratamentos teremos apenas 0, 2 ou 6 g.l., respectivamente,para o resíduo.
- Por outro lado, com 9 ou mais tratamentos, o quadrado latino fica muito grande, trazendo dificuldades na instalação, pois, para 9 tratamentos, teremos 81 parcelas.
- Por isso, os quadrados latinos mais usados são os de 5 x 5, 6 x 6, 7 x 7 e 8 x 8.
8.1.1 Modelo matemático
\[\begin{eqnarray} y_{ji}=\mu+\tau_i+\alpha_j+\beta_k+\varepsilon_{ij} \end{eqnarray}\]
\(y_{ji}\): é o valor observado na i-ésima linha e k-ésima coluna para o j-ésimo tratamento;
\(\mu\): é a média geral (ou constante comum a todas as observações);
\(\tau_i\): é o efeito de tratamento, com \(i = 1, 2, . . . , I\);
\(\beta_j\): é o efeito da k-ésima coluna;
\(\alpha_j\): é efeito da j-ésima linha
\(\varepsilon_{ij}\): é o erro experimental, tal que \(\varepsilon_{ij}\)~N(0; \(\sigma^2\)).
O modelo é completamente aditivo, ou seja, não há interação entre linhas, colunas e tratamentos.
8.1.2 Hipóteses e Modelo
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 =\mu_i\\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
| CV | G.L. | S.Q. | Q.M. | Fcalc | Ftab |
|---|---|---|---|---|---|
| Tratamentos | \(p - 1\) | \(SQ_{Trat}\) | \(\frac{SQ_{Trat}}{p-1}\) | \(\frac{QMTrat}{QMRes}\) | \(F(\alpha;GL_{Trat} ;GL_{Res})\) |
| Linhas | \(p - 1\) | \(SQ_{L}\) | \(\frac{SQ_{L}}{p-1}\) | \(\frac{QM_{L}}{QM_{Res}}\) | \(F(\alpha;GL_{L} ;GL_{Res})\) |
| Colunas | \(p - 1\) | \(SQ_{C}\) | \(\frac{SQ_{C}}{p-1}\) | \(\frac{QM_{C}}{QM_{Res}}\) | \(F(\alpha;GL_{C} ;GL_{Res})\) |
| resíduo | \((p-2)(p-1)\) | \(SQ_{Res}\) | \(\frac{SQRes}{(p-2)(p-1)}\) | ||
| Total | \(p^2-1\) | \(SQ_{Total}\) |
8.2 DQL
No AgroR, podemos realizar a análise de um experimento em quadrado latino pelo seguinte comando:
rm(list=ls())
data(porco)
with(porco,DQL(trat, linhas, colunas, resp))##
## -----------------------------------------------------------------
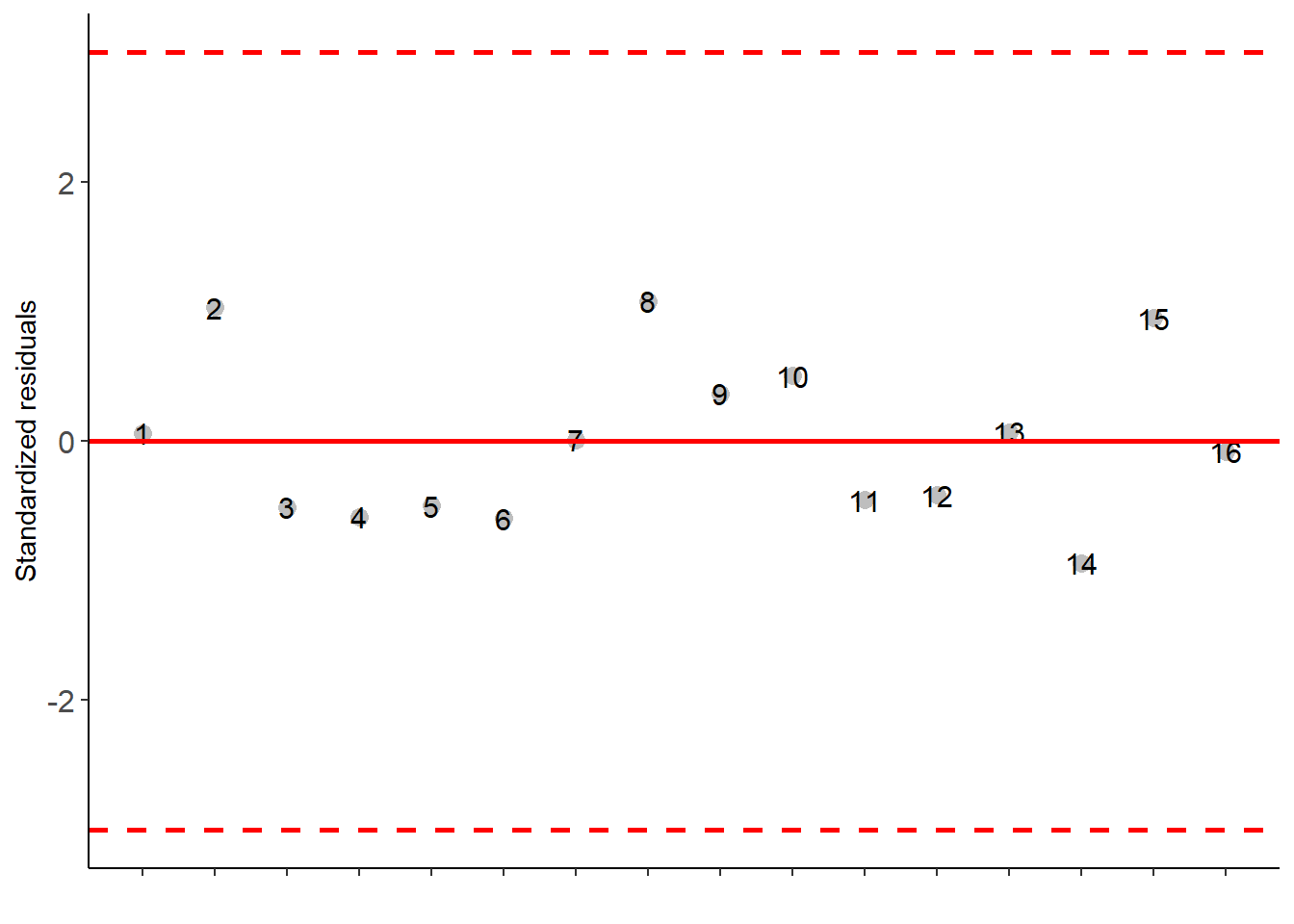
## Normality of errors (Shapiro-Wilk
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9183353 0.1585848## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 1.207666 0.7511662## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 2.028993 0.2932159## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 16
## R-squared = 0.1
## Mean = 3.4331
## Median = 3.39
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## trat 3 0.2622187 0.08740625 0.2898586 0.8315413
## line 3 0.1065687 0.03552292 0.1178019 0.9463594
## column 3 1.4274687 0.47582292 1.5779347 0.2899683
## Residuals 6 1.8092875 0.30154792## As the calculated p-value is greater than the 5% significance level, H0 is not rejected##
## -----------------------------------------------------------------
## Multiple Comparison Test
## -----------------------------------------------------------------
## [1] "H0 is not rejected"##