15 Regressões
15.1 polynomial
A análise de regressão polinomial até terceiro grau no caso de delineamento simples (DIC, DBC ou DQL) ou de efeito isolado do fator quantitativo no caso de arranjos fatoriais ou parcelas subdivididas podem ser realizadas ainda na própria função correspondendo, declarando o argumento quali como FALSE ao respectivo fator quantitativo. Todavia, há restrições quanto a alteração do layout gráfico nesses casos. Assim, é aconselhavel a utilização da função polynomial.
data("phao")
with(phao, polynomial(dose,comp, grau = 2))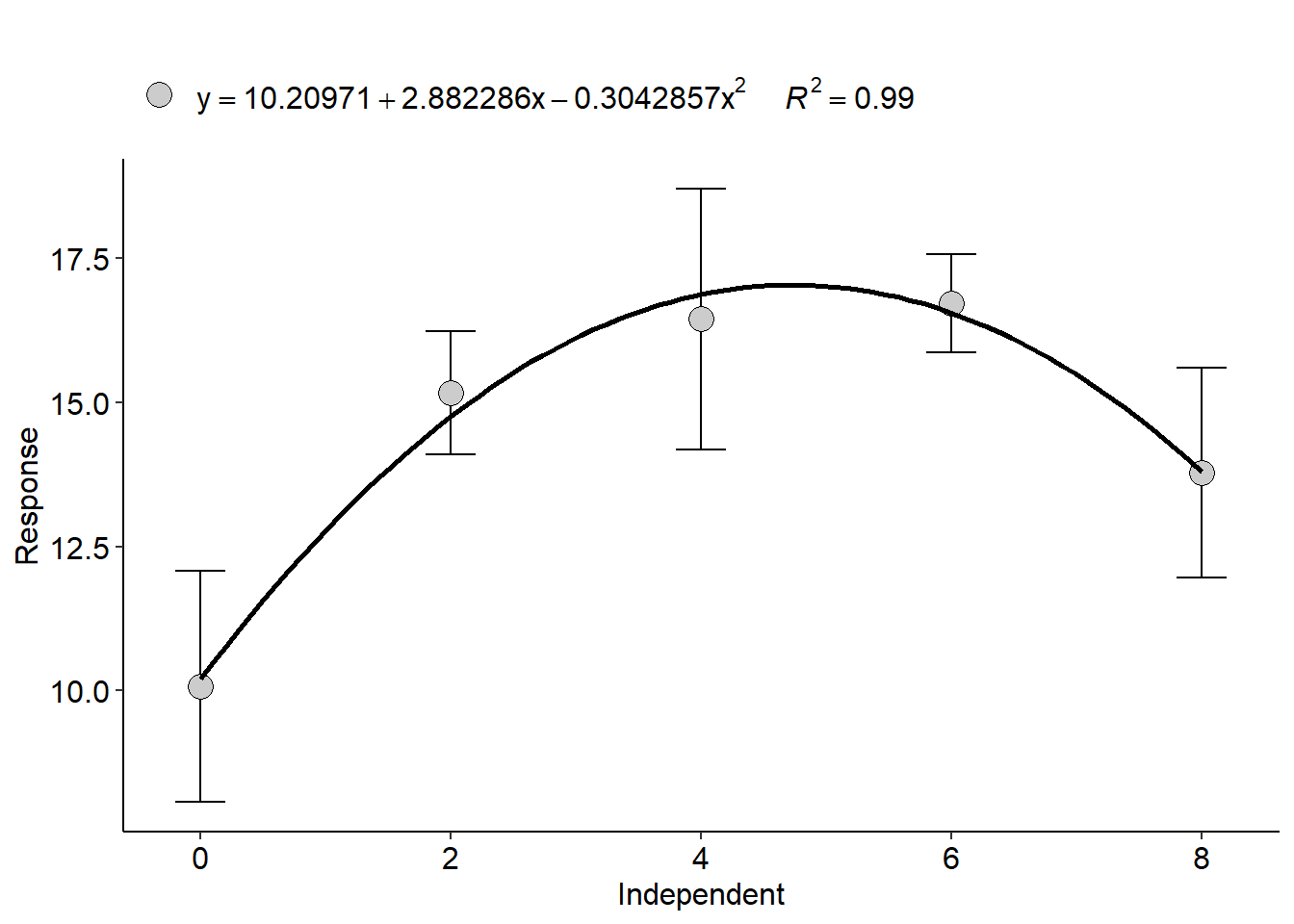
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.2097143 0.68981140 14.800733 6.427099e-13
## trat 2.8822857 0.40856781 7.054608 4.456995e-07
## I(trat^2) -0.3042857 0.04897332 -6.213296 2.971498e-06
##
## ----------------------------------------------------
## Deviations from regression
## ----------------------------------------------------
## GL SQ F p-value
## 2 1.968229 0.3445296 0.712676715.2 polynomial2
Assim como na função polynomial, há também a opção de usar a função polynomial2, que realiza a análise de regressão polinomial até terceiro grau no caso de delineamentos conduzidos em arranjos fatoriais ou parcelas subdivididas em um dos fatores é quantitativo e outro qualitativo.
dose=rep(c(0,0,0,2,2,2,4,4,4,6,6,6),3)
resp=c(8,7,5,23,24,25,30,34,36,80,90,80,12,14,15,23,24,25,50,54,56,80,90,40,
12,14,15,3,4,5,50,54,56,80,90,40)
trat=rep(c("A","B","C"),e=12)
polynomial2(dose, resp, trat, grau=c(1,2,3))##
## ----------------------------------------------------
## Regression Models
## ----------------------------------------------------
## $A
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.9333333 5.395430 0.1729859 8.661137e-01
## x 11.9666667 1.441989 8.2987205 8.528803e-06
##
## $B
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 12.0833333 7.4460094 1.6227932 0.1390822
## x 7.5416667 5.9788110 1.2613991 0.2388777
## I(x^2) 0.3958333 0.9549306 0.4145153 0.6882023
##
## $C
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13.666667 7.7064187 1.773413 0.11409087
## x -34.861111 14.7845901 -2.357936 0.04610656
## I(x^2) 18.833333 6.5334343 2.882609 0.02042957
## I(x^3) -1.909722 0.7180032 -2.659769 0.02881582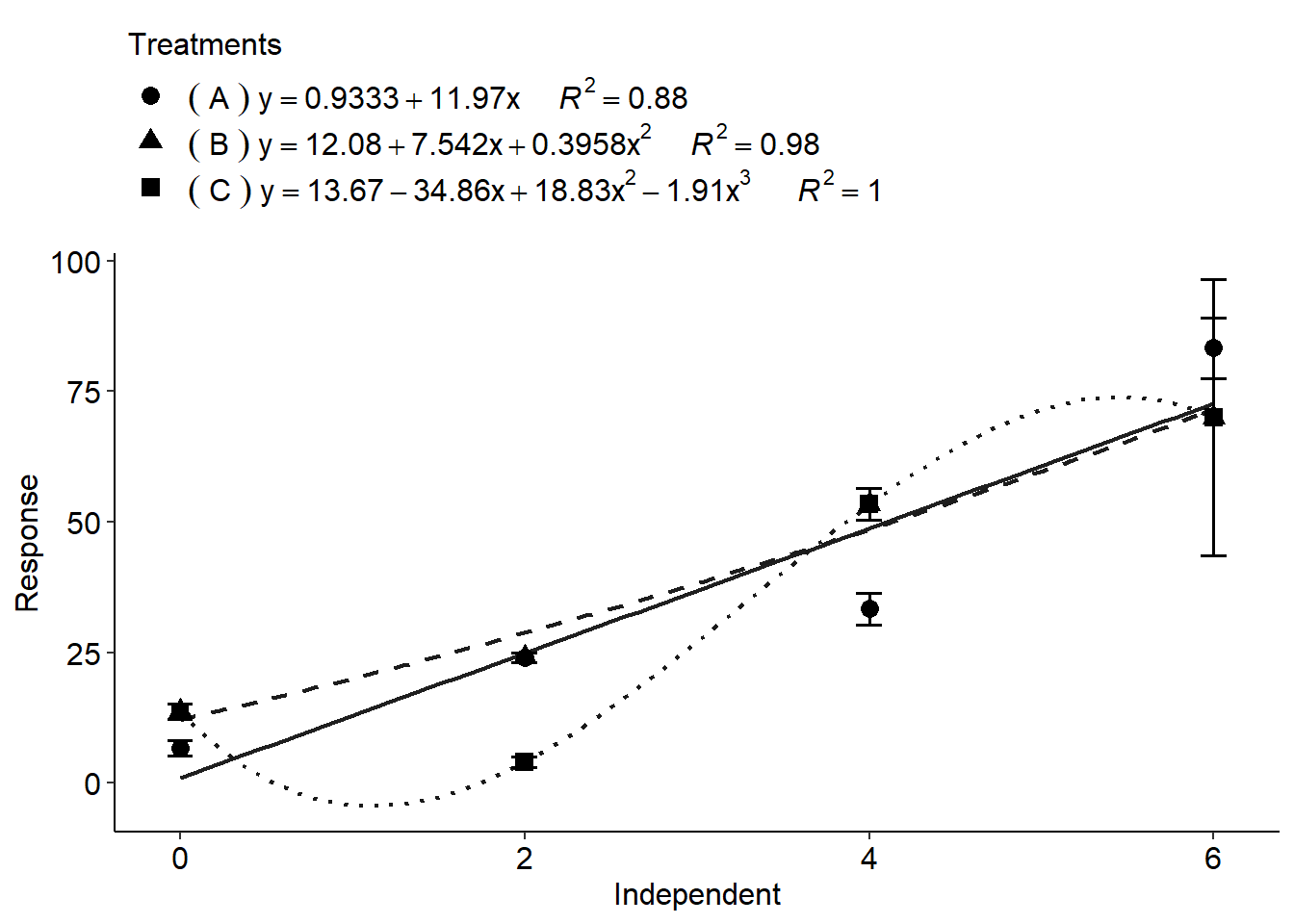
15.3 polynomial2_color
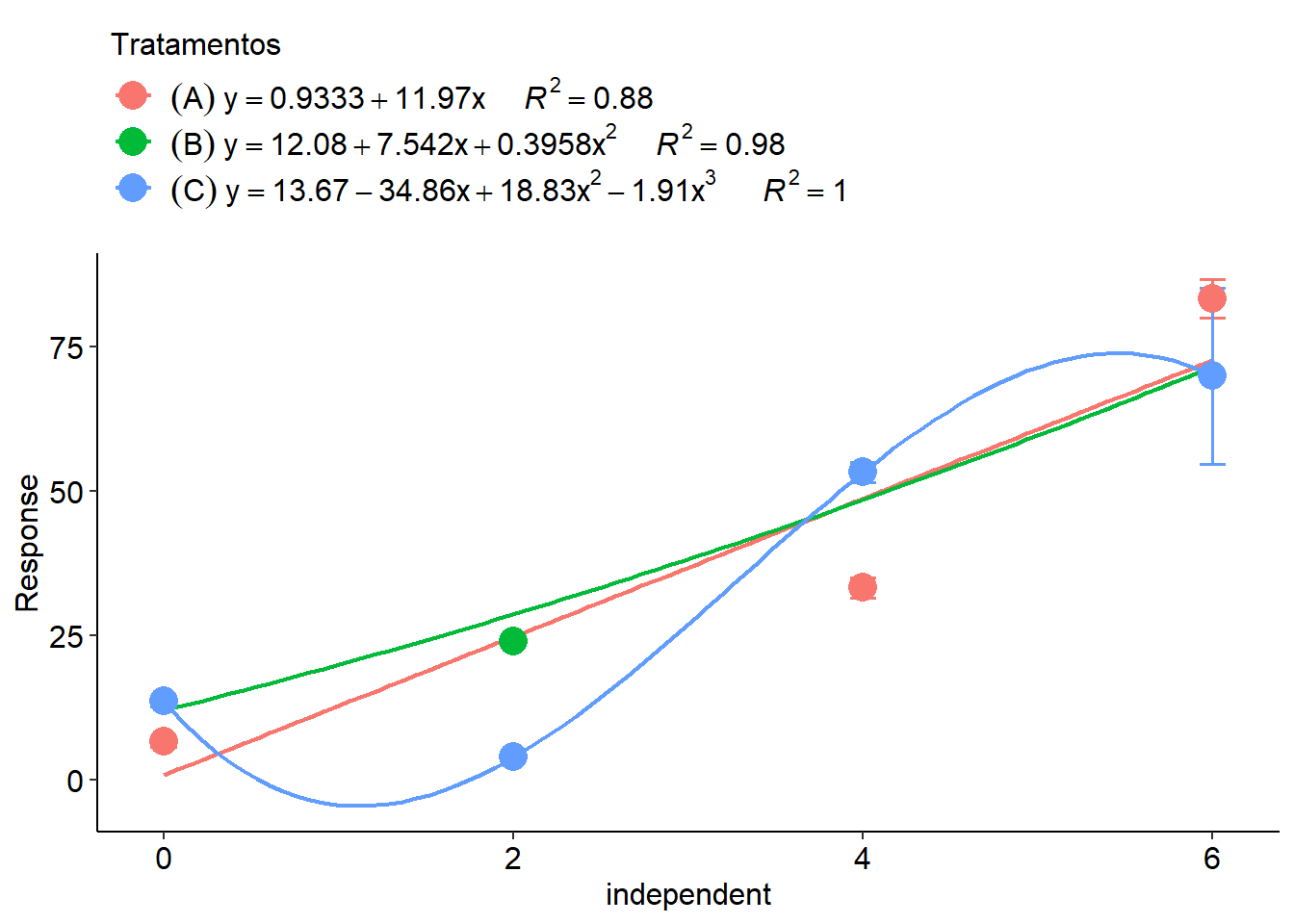
A função polynomial2_color realiza a mesma análise da função polynomial2, contudo, a saída gráfica apresenta diferenciação do fator qualitativo por coloração.
polynomial2_color(dose, resp, trat, grau=c(1,2,3))##
## ----------------------------------------------------
## Regression Models
## ----------------------------------------------------
## $A
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.9333333 5.395430 0.1729859 8.661137e-01
## x 11.9666667 1.441989 8.2987205 8.528803e-06
##
## $B
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 12.0833333 7.4460094 1.6227932 0.1390822
## x 7.5416667 5.9788110 1.2613991 0.2388777
## I(x^2) 0.3958333 0.9549306 0.4145153 0.6882023
##
## $C
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 13.666667 7.7064187 1.773413 0.11409087
## x -34.861111 14.7845901 -2.357936 0.04610656
## I(x^2) 18.833333 6.5334343 2.882609 0.02042957
## I(x^3) -1.909722 0.7180032 -2.659769 0.02881582