12 Fatorial triplo
12.1 Teoria
Nos experimentos mais simples comparamos níveis (tratamentos) de apenas um fator; entretanto, existem casos em que dois ou mais fatores devem ser estudados simultaneamente para que possam nos conduzir a resultados de interesse;
Em geral, os experimentos fatoriais são mais eficientes para este tipo de experimento, pois estudam, ao mesmo tempo, os efeitos de dois ou mais fatores, cada um deles com dois ou mais níveis.
O fatorial é um tipo de esquema, ou seja, uma das maneiras de organizar os tratamentos e não um tipo de delineamento;
Os experimentos fatoriais são montados segundo um tipo de delineamento experimental;
Nos experimentos fatoriais, os tratamentos são obtidos pelas combinações dos níveis dos fatores.
12.1.1 Tipos de efeitos avaliados
Efeito Principal: é o efeito de cada fator, independente do efeito dos outros fatores;
Efeito de Interação: é o efeito simultâneo dos fatores sobre a variável em estudo. Dizemos que ocorre interação entre os fatores quando os efeitos dos níveis de um fator são modificados pelos níveis do outro fator.
12.1.2 Vantagens
Pode-se estudar dois ou mais fatores num único experimento.
Pode-se, por meio dos efeitos das interações, verificar se um fator é independente ou dependente do(s) outro(s).
12.1.3 Desvantagens
O número de tratamentos ou combinações de níveis de fatores cresce, rapidamente, com o aumento do número de níveis, em cada fator, ou mesmo com o aumento do número de fatores.
A interpretação dos resultados se torna mais difícil é medida que aumentamos o número de níveis e de fatores no experimento.
12.1.4 Modelo estatístico
As observações podem ser descritas pelo modelo estatístico linear:
\(y_{ijk} = \mu+\beta_{1i}+\beta_{2j}+\beta_{3k}+(\beta_1\beta_2)_{ij}+(\beta_1\beta_3)_{ik}+(\beta_2\beta_3)_{jk}+(\beta_1\beta_2\beta_3)_{ijk}+\epsilon_{ijk}\)
- i = 1; 2; : : : ; a
- j = 1; 2; : : : ; b
- k = 1; 2; : : : ; c
em que:
- \(y_{ijk}\) é o valor observado no i-ésimo nível do fator A, j-ésima nível do fator B e k-ésimo nível do fator C;
- \(\mu\) é uma constante;
- \(\beta_{1i}\) é o efeito do i-ésimo nível do fator A;
- \(\beta_{2j}\) é o efeito do j-ésimo nível do fator B;
- \(\beta_{3k}\) é o efeito do j-ésimo nível do fator C;
- \((\beta_1\beta_2)_ij\) é o efeito da interação entre \(\beta_{1i}\) e \(\beta_{2j}\);
- \((\beta_1\beta_3)_ik\) é o efeito da interação entre \(\beta_{1i}\) e \(\beta_{3j}\);
- \((\beta_2\beta_3)_jk\) é o efeito da interação entre \(\beta_{2i}\) e \(\beta_{3j}\);
- \((\beta_1\beta_2\beta_3)_{ijk}\) é o efeito da interação entre \(\beta_{1i}\), \(\beta_{2j}\) e \(\beta_{3k}\);
- \((\epsilon)ijk\) é o componente de erro aleatório.
12.1.5 Hipóteses e modelo
No experimento fatorial com 3 fatores, deseja-se testar a signicância de ambos os fatores.
No experimento fatorial com 2 fatores, deseja-se testar a signicância de ambos os fatores.
Há interesse em testar hipóteses sobre a igualdade dos efeitos do fator A, isto é:
- H0 : \(\beta_{11}\) = \(\beta_{12}\) = : : : \(\beta_{1a}\) = 0
- H1 : Pelo menos um \(\beta_{1i} \neq 0\)
e a igualdade nos efeitos do fator B, ou seja:
- H0 : \(\beta_{21}\) = \(\beta_{22}\) = : : : \(\beta_{2b}\) = 0
- H1 : Pelo menos um \(\beta_{2j} \neq 0\)
e, ainda, se há interação entre os fatores A e B:
- H0 : \((\beta_1\beta_2)_{ij}\) = 0 para todo i ; j
- H1 : Pelo menos um \((\beta_1\beta_2)_{ij} \neq 0\)
e, ainda, se há interação entre os fatores A e C:
- H0 : \((\beta_1\beta_3)_{ik}\) = 0 para todo i ; k
- H1 : Pelo menos um \((\beta_1\beta_3)_{ik} \neq 0\)
e, ainda, se há interação entre os fatores B e C:
- H0 : \((\beta_2\beta_3)_{jk}\) = 0 para todo j ; k
- H1 : Pelo menos um \((\beta_2\beta_3)_{jk} \neq 0\)
e, ainda, se há interação entre os fatores A e B e C:
- H0 : \((\beta_1\beta_2\beta_3)_{ijk}\) = 0 para todo i ; j; k
- H1 : Pelo menos um \((\beta_1\beta_2\beta_3)_{ijk} \neq 0\)
12.2 FAT3DIC
data(enxofre)
with(enxofre, FAT3DIC(f1, f2, f3, resp))##
## ------------------------------------------
## Normality of errors
## ------------------------------------------
##
## Shapiro-Wilk normality test
##
## data: anava$residuals
## W = 0.98386, p-value = 0.217## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## ------------------------------------------
## Homogeneity of Variances
## ------------------------------------------
##
## Bartlett test of homogeneity of variances
##
## data: anava$residuals by paste(Fator1, Fator2, Fator3)
## Bartlett's K-squared = 26.434, df = 26, p-value = 0.4394## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## ------------------------------------------
## Independence from errors
## ------------------------------------------
##
## Durbin-Watson test
##
## data: anava
## DW = 2.8115, p-value = 0.9728
## alternative hypothesis: true autocorrelation is greater than 0## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 6.61
## Mean = 4985.6044
## Median = 4975.775
## Possible outliers = No discrepant point
##
## ------------------------------------------
## Analysis of Variance
## ------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## Fator1 2 532880.7 266440.4 2.455006 9.222958e-02
## Fator2 2 2593572.1 1296786.1 11.948706 2.835764e-05
## Fator3 2 1012836.0 506418.0 4.666182 1.207777e-02
## Fator1:Fator2 4 568195.7 142048.9 1.308852 2.737151e-01
## Fator1:Fator3 4 2177620.9 544405.2 5.016200 1.157565e-03
## Fator2:Fator3 4 548172.3 137043.1 1.262728 2.914782e-01
## Fator1:Fator2:Fator3 8 2255321.1 281915.1 2.597592 1.400982e-02
## Residuals 81 8790882.9 108529.4## 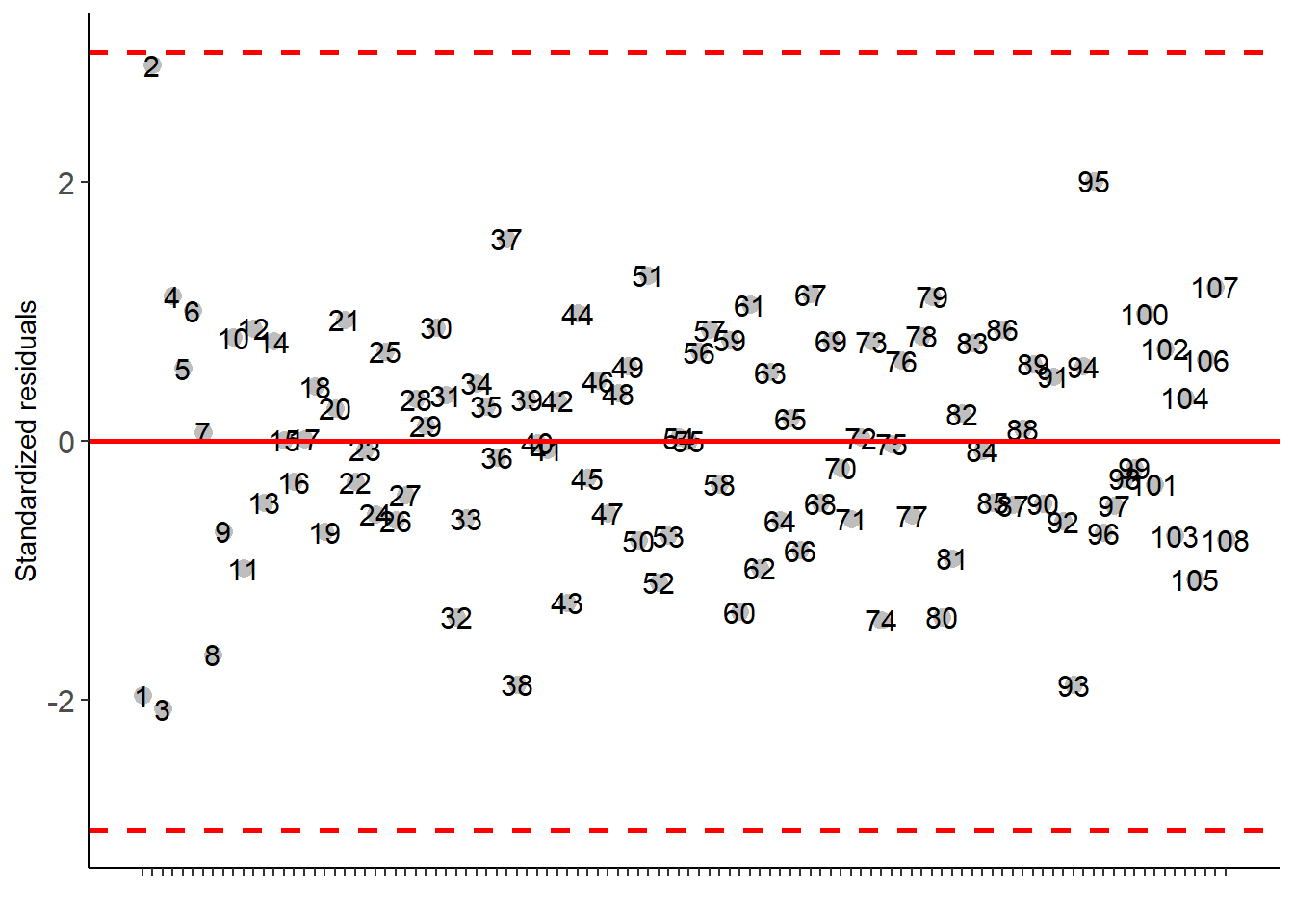
##
## ------------------------------------------
## Interaction F1*F2*F3 significant: unfolding the interaction
## ------------------------------------------
##
## ------------------------------------------
## Analyzing F1 inside of each level of F2 and F3
## ------------------------------------------
## Df Sum Sq Mean Sq F value
## Fator2: 150 Fator3: Vegetativo 2 1515236.80 757618.40 6.9807653
## Fator2: 450 Fator3: Vegetativo 2 1485001.57 742500.78 6.8414702
## Fator2: 1350 Fator3: Vegetativo 2 355299.69 177649.85 1.6368820
## Fator2: 150 Fator3: Ciclo Completo 2 110556.18 55278.09 0.5093374
## Fator2: 450 Fator3: Ciclo Completo 2 509409.88 254704.94 2.3468747
## Fator2: 1350 Fator3: Ciclo Completo 2 63027.18 31513.59 0.2903691
## Fator2: 150 Fator3: Reprodutivo 2 1100604.58 550302.29 5.0705357
## Fator2: 450 Fator3: Reprodutivo 2 195182.15 97591.07 0.8992131
## Fator2: 1350 Fator3: Reprodutivo 2 199700.39 99850.20 0.9200289
## Pr(>F)
## Fator2: 150 Fator3: Vegetativo 0.001595736
## Fator2: 450 Fator3: Vegetativo 0.001797372
## Fator2: 1350 Fator3: Vegetativo 0.200956205
## Fator2: 150 Fator3: Ciclo Completo 0.602805170
## Fator2: 450 Fator3: Ciclo Completo 0.102141658
## Fator2: 1350 Fator3: Ciclo Completo 0.748762716
## Fator2: 150 Fator3: Reprodutivo 0.008418234
## Fator2: 450 Fator3: Reprodutivo 0.410912121
## Fator2: 1350 Fator3: Reprodutivo 0.402631134
##
## F1 within the combination of levels 150 of F2 and Vegetativo of F3
## resp letters
## 75 5246.363 a
## 675 4578.007 b
## 225 4429.288 b
##
## F1 within the combination of levels 150 of F2 and Ciclo Completo of F3
## resp letters
## 675 5027.233 a
## 225 4927.000 a
## 75 4792.932 a
##
## F1 within the combination of levels 150 of F2 and Reprodutivo of F3
## resp letters
## 675 5056.610 a
## 225 4847.748 ab
## 75 4335.730 b
##
## F1 within the combination of levels 450 of F2 and Vegetativo of F3
## resp letters
## 75 5286.368 a
## 225 5125.075 a
## 675 4472.670 b
##
## F1 within the combination of levels 450 of F2 and Ciclo Completo of F3
## resp letters
## 75 5389.980 a
## 675 5085.130 a
## 225 4889.233 a
##
## F1 within the combination of levels 450 of F2 and Reprodutivo of F3
## resp letters
## 675 4968.540 a
## 75 4847.222 a
## 225 4658.573 a
##
## F1 within the combination of levels 1350 of F2 and Vegetativo of F3
## resp letters
## 75 5561.840 a
## 675 5355.302 a
## 225 5140.382 a
##
## F1 within the combination of levels 1350 of F2 and Ciclo Completo of F3
## resp letters
## 75 5305.762 a
## 675 5188.823 a
## 225 5131.625 a
##
## F1 within the combination of levels 1350 of F2 and Reprodutivo of F3
## resp letters
## 225 5147.488 a
## 75 4984.855 a
## 675 4831.542 a
##
##
##
## ------------------------------------------
## Analyzing F2 inside of each level of F1 and F3
## ------------------------------------------
## Df Sum Sq Mean Sq F value
## Fator1: 75 Fator3: Vegetativo 2 236015.40 118007.70 1.0873338
## Fator1: 225 Fator3: Vegetativo 2 1320014.22 660007.11 6.0813660
## Fator1: 675 Fator3: Vegetativo 2 1859098.18 929549.09 8.5649505
## Fator1: 75 Fator3: Ciclo Completo 2 835403.88 417701.94 3.8487440
## Fator1: 225 Fator3: Ciclo Completo 2 136069.20 68034.60 0.6268770
## Fator1: 675 Fator3: Ciclo Completo 2 53620.78 26810.39 0.2470334
## Fator1: 75 Fator3: Reprodutivo 2 935907.40 467953.70 4.3117682
## Fator1: 225 Fator3: Reprodutivo 2 486225.50 243112.75 2.2400631
## Fator1: 675 Fator3: Reprodutivo 2 102906.69 51453.35 0.4740958
## Pr(>F)
## Fator1: 75 Fator3: Vegetativo 0.3419832110
## Fator1: 225 Fator3: Vegetativo 0.0034620517
## Fator1: 675 Fator3: Vegetativo 0.0004223652
## Fator1: 75 Fator3: Ciclo Completo 0.0253066587
## Fator1: 225 Fator3: Ciclo Completo 0.5368293731
## Fator1: 675 Fator3: Ciclo Completo 0.7817009516
## Fator1: 75 Fator3: Reprodutivo 0.0166168673
## Fator1: 225 Fator3: Reprodutivo 0.1130067748
## Fator1: 675 Fator3: Reprodutivo 0.6241638200
##
##
## F2 within the combination of levels 75 of F1 and Vegetativo of F3
## resp letters
## 1350 5561.840 a
## 450 5286.368 a
## 150 5246.363 a
##
##
## F2 within the combination of levels 75 of F1 and Ciclo Completo of F3
## resp letters
## 450 5389.980 a
## 1350 5305.762 ab
## 150 4792.932 b
##
##
## F2 within the combination of levels 75 of F1 and Reprodutivo of F3
## resp letters
## 1350 4984.855 a
## 450 4847.222 ab
## 150 4335.730 b
##
##
## F2 within the combination of levels 225 of F1 and Vegetativo of F3
## resp letters
## 1350 5140.382 a
## 450 5125.075 a
## 150 4429.288 b
##
##
## F2 within the combination of levels 225 of F1 and Ciclo Completo of F3
## resp letters
## 1350 5131.625 a
## 150 4927.000 a
## 450 4889.233 a
##
##
## F2 within the combination of levels 225 of F1 and Reprodutivo of F3
## resp letters
## 1350 5147.488 a
## 150 4847.748 a
## 450 4658.573 a
##
##
## F2 within the combination of levels 675 of F1 and Vegetativo of F3
## resp letters
## 1350 5355.302 a
## 150 4578.007 b
## 450 4472.670 b
##
##
## F2 within the combination of levels 675 of F1 and Ciclo Completo of F3
## resp letters
## 1350 5188.823 a
## 450 5085.130 a
## 150 5027.233 a
##
##
## F2 within the combination of levels 675 of F1 and Reprodutivo of F3
## resp letters
## 150 5056.610 a
## 450 4968.540 a
## 1350 4831.542 a
##
## ------------------------------------------
## Analyzing F3 inside of each level of F1 and F2
## ------------------------------------------
## Df Sum Sq Mean Sq F value Pr(>F)
## Fator1: 75 Fator2: 150 2 1658512.5879 829256.2940 7.640843446 0.0009122708
## Fator1: 225 Fator2: 150 2 572143.2840 286071.6420 2.635890311 0.0777962047
## Fator1: 675 Fator2: 150 2 575635.3215 287817.6608 2.651978288 0.0766301475
## Fator1: 75 Fator2: 450 2 664226.1133 332113.0567 3.060120123 0.0523384862
## Fator1: 225 Fator2: 450 2 435267.0705 217633.5353 2.005295327 0.1412490062
## Fator1: 675 Fator2: 450 2 846116.7155 423058.3577 3.898098457 0.0241919824
## Fator1: 75 Fator2: 1350 2 668625.3331 334312.6665 3.080387530 0.0513616993
## Fator1: 225 Fator2: 1350 2 505.0583 252.5292 0.002326827 0.9976759449
## Fator1: 675 Fator2: 1350 2 572918.8352 286459.4176 2.639463311 0.0775356725
##
##
## F3 within the combination of levels 75 of F1 and 150 of F2
## resp letters
## Vegetativo 5246.363 a
## Ciclo Completo 4792.932 ab
## Reprodutivo 4335.730 b
##
##
## F3 within the combination of levels 75 of F1 and 450 of F2
## resp letters
## Ciclo Completo 5389.980 a
## Vegetativo 5286.368 a
## Reprodutivo 4847.222 a
##
##
## F3 within the combination of levels 75 of F1 and 1350 of F2
## resp letters
## Vegetativo 5561.840 a
## Ciclo Completo 5305.762 ab
## Reprodutivo 4984.855 b
##
##
## F3 within the combination of levels 225 of F1 and 150 of F2
## resp letters
## Ciclo Completo 4927.000 a
## Reprodutivo 4847.748 a
## Vegetativo 4429.288 a
##
##
## F3 within the combination of levels 225 of F1 and 450 of F2
## resp letters
## Vegetativo 5125.075 a
## Ciclo Completo 4889.233 a
## Reprodutivo 4658.573 a
##
##
## F3 within the combination of levels 225 of F1 and 1350 of F2
## resp letters
## Reprodutivo 5147.488 a
## Vegetativo 5140.382 a
## Ciclo Completo 5131.625 a
##
##
## F3 within the combination of levels 675 of F1 and 150 of F2
## resp letters
## Reprodutivo 5056.610 a
## Ciclo Completo 5027.233 a
## Vegetativo 4578.007 a
##
##
## F3 within the combination of levels 675 of F1 and 450 of F2
## resp letters
## Ciclo Completo 5085.13 a
## Reprodutivo 4968.54 ab
## Vegetativo 4472.67 b
##
##
## F3 within the combination of levels 675 of F1 and 1350 of F2
## resp letters
## Vegetativo 5355.302 a
## Ciclo Completo 5188.823 a
## Reprodutivo 4831.542 a12.3 FAT3DBC
data(enxofre)
with(enxofre, FAT3DBC(f1, f2, f3, bloco, resp))##
## ------------------------------------------
## Normality of errors
## ------------------------------------------
## Shapiro-Wilk normality test
##
## data: anava$residuals
## W = 0.989, p-value = 0.5281## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## ------------------------------------------
## Homogeneity of Variances
## ------------------------------------------
## Bartlett test of homogeneity of variances
##
## data: anava$residuals by paste(Fator1, Fator2, Fator3)
## Bartlett's K-squared = 25.924, df = 26, p-value = 0.4673## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## ------------------------------------------
## Independence from errors
## ------------------------------------------
## Durbin-Watson test
##
## data: anava
## DW = 2.824, p-value = 0.9766
## alternative hypothesis: true autocorrelation is greater than 0## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 6.67
## Mean = 4985.6044
## Median = 4975.775
## Possible outliers = No discrepant point
##
## ------------------------------------------
## Analysis of Variance
## ------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## Fator1 2 532880.7 266440.37 2.4098282 9.649081e-02
## Fator2 2 2593572.1 1296786.07 11.7288222 3.520329e-05
## Fator3 2 1012836.0 506417.98 4.5803133 1.315819e-02
## bloco 3 166887.1 55629.03 0.5031385 6.812289e-01
## Fator1:Fator2 4 568195.7 142048.92 1.2847659 2.832261e-01
## Fator1:Fator3 4 2177620.9 544405.23 4.9238901 1.361837e-03
## Fator2:Fator3 4 548172.3 137043.08 1.2394905 3.011456e-01
## Fator1:Fator2:Fator3 8 2255321.1 281915.14 2.5497903 1.598465e-02
## Residuals 78 8623995.8 110564.05## 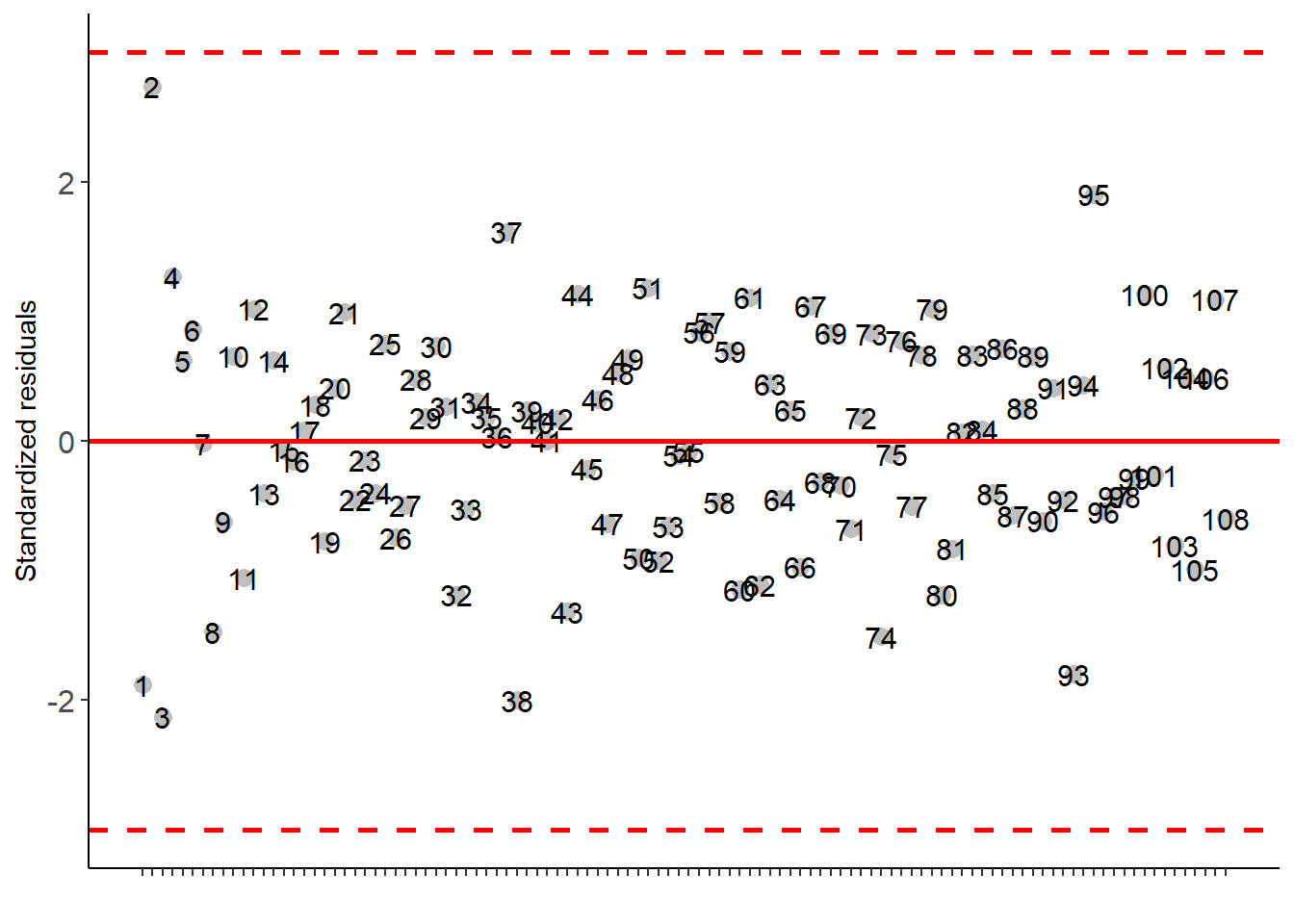
##
## ------------------------------------------
##
## Interaction F1*F2*F3 significant: unfolding the interaction
##
## ------------------------------------------
##
## ------------------------------------------
## Analyzing F1 within the combination of levels F2 and F3
## ------------------------------------------
## Df Sum Sq Mean Sq F value
## Fator2: 150 Fator3: Vegetativo 2 1515236.80 757618.40 6.8523034
## Fator2: 450 Fator3: Vegetativo 2 1485001.57 742500.78 6.7155716
## Fator2: 1350 Fator3: Vegetativo 2 355299.69 177649.85 1.6067596
## Fator2: 150 Fator3: Ciclo Completo 2 110556.18 55278.09 0.4999644
## Fator2: 450 Fator3: Ciclo Completo 2 509409.88 254704.94 2.3036868
## Fator2: 1350 Fator3: Ciclo Completo 2 63027.18 31513.59 0.2850257
## Fator2: 150 Fator3: Reprodutivo 2 1100604.58 550302.29 4.9772263
## Fator2: 450 Fator3: Reprodutivo 2 195182.15 97591.07 0.8826655
## Fator2: 1350 Fator3: Reprodutivo 2 199700.39 99850.20 0.9030982
## Pr(>F)
## Fator2: 150 Fator3: Vegetativo 0.001813153
## Fator2: 450 Fator3: Vegetativo 0.002037125
## Fator2: 1350 Fator3: Vegetativo 0.207102162
## Fator2: 150 Fator3: Ciclo Completo 0.608482641
## Fator2: 450 Fator3: Ciclo Completo 0.106648740
## Fator2: 1350 Fator3: Ciclo Completo 0.752774794
## Fator2: 150 Fator3: Reprodutivo 0.009239195
## Fator2: 450 Fator3: Reprodutivo 0.417769568
## Fator2: 1350 Fator3: Reprodutivo 0.409507252
##
##
## F1 inside of each level of 150 of F2 and Vegetativo of F3
## resp letters
## 75 5246.363 a
## 675 4578.007 b
## 225 4429.288 b
##
##
## F1 inside of each level of 150 of F2 and Ciclo Completo of F3
## resp letters
## 675 5027.233 a
## 225 4927.000 a
## 75 4792.932 a
##
##
## F1 inside of each level of 150 of F2 and Reprodutivo of F3
## resp letters
## 675 5056.610 a
## 225 4847.748 ab
## 75 4335.730 b
##
##
## F1 inside of each level of 450 of F2 and Vegetativo of F3
## resp letters
## 75 5286.368 a
## 225 5125.075 a
## 675 4472.670 b
##
##
## F1 inside of each level of 450 of F2 and Ciclo Completo of F3
## resp letters
## 75 5389.980 a
## 675 5085.130 a
## 225 4889.233 a
##
##
## F1 inside of each level of 450 of F2 and Reprodutivo of F3
## resp letters
## 675 4968.540 a
## 75 4847.222 a
## 225 4658.573 a
##
##
## F1 inside of each level of 1350 of F2 and Vegetativo of F3
## resp letters
## 75 5561.840 a
## 675 5355.302 a
## 225 5140.382 a
##
##
## F1 inside of each level of 1350 of F2 and Ciclo Completo of F3
## resp letters
## 75 5305.762 a
## 675 5188.823 a
## 225 5131.625 a
##
##
## F1 inside of each level of 1350 of F2 and Reprodutivo of F3
## resp letters
## 225 5147.488 a
## 75 4984.855 a
## 675 4831.542 a
##
##
##
## ------------------------------------------
## Analyzing F2 within the combination of levels F1 and F3
## ------------------------------------------
## Df Sum Sq Mean Sq F value
## Fator1: 75 Fator3: Vegetativo 2 236015.40 118007.70 1.0673243
## Fator1: 225 Fator3: Vegetativo 2 1320014.22 660007.11 5.9694550
## Fator1: 675 Fator3: Vegetativo 2 1859098.18 929549.09 8.4073359
## Fator1: 75 Fator3: Ciclo Completo 2 835403.88 417701.94 3.7779183
## Fator1: 225 Fator3: Ciclo Completo 2 136069.20 68034.60 0.6153411
## Fator1: 675 Fator3: Ciclo Completo 2 53620.78 26810.39 0.2424874
## Fator1: 75 Fator3: Reprodutivo 2 935907.40 467953.70 4.2324219
## Fator1: 225 Fator3: Reprodutivo 2 486225.50 243112.75 2.1988409
## Fator1: 675 Fator3: Reprodutivo 2 102906.69 51453.35 0.4653714
## Pr(>F)
## Fator1: 75 Fator3: Vegetativo 0.3488962873
## Fator1: 225 Fator3: Vegetativo 0.0038701904
## Fator1: 675 Fator3: Vegetativo 0.0004937911
## Fator1: 75 Fator3: Ciclo Completo 0.0271614813
## Fator1: 225 Fator3: Ciclo Completo 0.5430591078
## Fator1: 675 Fator3: Ciclo Completo 0.7852629386
## Fator1: 75 Fator3: Reprodutivo 0.0179864982
## Fator1: 225 Fator3: Reprodutivo 0.1177618911
## Fator1: 675 Fator3: Reprodutivo 0.6296338939
##
##
## F2 inside of each level of 75 of F1 and Vegetativo of F3
## resp letters
## 1350 5561.840 a
## 450 5286.368 a
## 150 5246.363 a
##
##
## F2 inside of each level of 75 of F1 and Ciclo Completo of F3
## resp letters
## 450 5389.980 a
## 1350 5305.762 ab
## 150 4792.932 b
##
##
## F2 inside of each level of 75 of F1 and Reprodutivo of F3
## resp letters
## 1350 4984.855 a
## 450 4847.222 ab
## 150 4335.730 b
##
##
## F2 inside of each level of 225 of F1 and Vegetativo of F3
## resp letters
## 1350 5140.382 a
## 450 5125.075 a
## 150 4429.288 b
##
##
## F2 inside of each level of 225 of F1 and Ciclo Completo of F3
## resp letters
## 1350 5131.625 a
## 150 4927.000 a
## 450 4889.233 a
##
##
## F2 inside of each level of 225 of F1 and Reprodutivo of F3
## resp letters
## 1350 5147.488 a
## 150 4847.748 a
## 450 4658.573 a
##
##
## F2 inside of each level of 675 of F1 and Vegetativo of F3
## resp letters
## 1350 5355.302 a
## 150 4578.007 b
## 450 4472.670 b
##
##
## F2 inside of each level of 675 of F1 and Ciclo Completo of F3
## resp letters
## 1350 5188.823 a
## 450 5085.130 a
## 150 5027.233 a
##
##
## F2 inside of each level of 675 of F1 and Reprodutivo of F3
## resp letters
## 150 5056.610 a
## 450 4968.540 a
## 1350 4831.542 a
##
## ------------------------------------------
## Analyzing F3 within the combination of levels F1 and F2
## ------------------------------------------
## Df Sum Sq Mean Sq F value Pr(>F)
## Fator1: 75 Fator2: 150 2 1658512.5879 829256.2940 7.500234535 0.001048985
## Fator1: 225 Fator2: 150 2 572143.2840 286071.6420 2.587383930 0.081661472
## Fator1: 675 Fator2: 150 2 575635.3215 287817.6608 2.603175851 0.080461250
## Fator1: 75 Fator2: 450 2 664226.1133 332113.0567 3.003806948 0.055368426
## Fator1: 225 Fator2: 450 2 435267.0705 217633.5353 1.968393329 0.146558601
## Fator1: 675 Fator2: 450 2 846116.7155 423058.3577 3.826364573 0.025988577
## Fator1: 75 Fator2: 1350 2 668625.3331 334312.6665 3.023701388 0.054355301
## Fator1: 225 Fator2: 1350 2 505.0583 252.5292 0.002284008 0.997718665
## Fator1: 675 Fator2: 1350 2 572918.8352 286459.4176 2.590891179 0.081393337
##
##
## F3 inside of each level of 75 of F1 and 150 of F2
## resp letters
## Vegetativo 5246.363 a
## Ciclo Completo 4792.932 ab
## Reprodutivo 4335.730 b
##
##
## F3 inside of each level of 75 of F1 and 450 of F2
## resp letters
## Ciclo Completo 5389.980 a
## Vegetativo 5286.368 a
## Reprodutivo 4847.222 a
##
##
## F3 inside of each level of 75 of F1 and 1350 of F2
## resp letters
## Vegetativo 5561.840 a
## Ciclo Completo 5305.762 ab
## Reprodutivo 4984.855 b
##
##
## F3 inside of each level of 225 of F1 and 150 of F2
## resp letters
## Ciclo Completo 4927.000 a
## Reprodutivo 4847.748 a
## Vegetativo 4429.288 a
##
##
## F3 inside of each level of 225 of F1 and 450 of F2
## resp letters
## Vegetativo 5125.075 a
## Ciclo Completo 4889.233 a
## Reprodutivo 4658.573 a
##
##
## F3 inside of each level of 225 of F1 and 1350 of F2
## resp letters
## Reprodutivo 5147.488 a
## Vegetativo 5140.382 a
## Ciclo Completo 5131.625 a
##
##
## F3 inside of each level of 675 of F1 and 150 of F2
## resp letters
## Reprodutivo 5056.610 a
## Ciclo Completo 5027.233 a
## Vegetativo 4578.007 a
##
##
## F3 inside of each level of 675 of F1 and 450 of F2
## resp letters
## Ciclo Completo 5085.13 a
## Reprodutivo 4968.54 ab
## Vegetativo 4472.67 b
##
##
## F3 inside of each level of 675 of F1 and 1350 of F2
## resp letters
## Vegetativo 5355.302 a
## Ciclo Completo 5188.823 a
## Reprodutivo 4831.542 a