7 Delineamento em blocos casualizados
7.1 Teoria
- O delineamento em blocos ao acaso ou o delineamento em blocos casualizados são aqueles que levam em consideração os 3 princípios básicos da experimentação;
- O controle local é feito na sua forma mais simples e é chamado de blocos;
- Sempre que não houver homogeneidade das condições experimentais, deve-se utilizar o princípio do controle local;
- Estabelece-se, então, sub-ambientes homogêneos (blocos) e instalando, em cada um deles, todos os tratamentos, igualmente repetidos;
- Nessas condições, o delineamento em blocos casualizados é mais eficiente que o inteiramente ao acaso e, essa eficiência depende da uniformidade das parcelas de cada bloco;
- Pode-se haver diferenças bem acentuadas de um bloco para outro.
- O número de blocos e de repetições coincide apenas quando os tratamentos ocorrem uma única vez em cada bloco.
7.1.1 Vantagens
- Controla as diferenças que ocorrem nas condições ambientais, de um bloco para outro;
- Conduz a uma estimativa mais exata para a variância residual, uma vez que a variação ambiental entre blocos é isolada.
7.1.2 Desvantagens
- Pela utilização do princípio do controle local, há uma redução no número de graus de liberdade do resíduo;
- Exigência de homogeneidade das parcelas dentro de cada bloco limita o número de tratamentos, que não pode ser muito elevado.
7.1.3 Modelo matemático
\[\begin{eqnarray} y_{ji}=\mu+\tau_i+\beta_j+\varepsilon_{ij} \end{eqnarray}\]
\(y_{ji}\): é a observação referente ao tratamento i no bloco j;
\(\mu\): é a média geral (ou constante comum a todas as observações);
\(\tau_i\): é o efeito de tratamento, com \(i = 1, 2, . . . , I\);
\(\beta_j\): é o efeito do bloco;
\(\varepsilon_{ij}\): é o erro experimental, tal que \(\varepsilon_{ij}\)~N(0; \(\sigma^2\)).
7.1.4 Hipóteses e Modelo
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 =\mu_i\\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
| CV | G.L. | S.Q. | Q.M. | Fcalc | Ftab |
|---|---|---|---|---|---|
| Tratamentos | \(a - 1\) | \(SQ_{Trat}\) | \(\frac{SQ_{Trat}}{a-1}\) | \(\frac{QMTrat}{QMRes}\) | \(F(\alpha;GL_{Trat} ;GL_{Res})\) |
| Blocos | \(b-1\) | \(Sq_{Blocos}\) | \(\frac{SQ_{Blocos}}{b-1}\) | \(\frac{QM_{bloco}}{QM_{Res}}\) | \(F(\alpha;GL_{bloco} ;GL_{Res})\) |
| resíduo | \((a-1)(b-1)\) | \(SQ_{Res}\) | \(\frac{SQRes}{(a-1)(b-1)}\) | - | |
| Total | \(ab-1\) | \(SQ_{Total}\) | - | - |
7.2 DBC
No pacote AgroR, os argumentos para DBC e DQL são muito similares a função DIC. A diferença está apenas na inserção do argumento block e da alteração do teste não-paramétrico para Friedman.
rm(list=ls())
data(laranja)
with(laranja, DBC(trat, bloco, resp,angle=45,
ylab = "Number of fruits/plants"))##
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9475889 0.187264## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 4.036888 0.85378## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 2.324604 0.2484349## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 8.69
## R-squared = 0.91
## Mean = 182.5556
## Median = 183
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## trat 8 22981.33333 2872.66667 11.41142069 2.636524e-05
## bloco 2 33.55556 16.77778 0.06664828 9.357825e-01
## Residuals 16 4027.77778 251.73611## As the calculated p-value, it is less than the 5% significance level. The hypothesis H0 of equality of means is rejected. Therefore, at least two treatments differ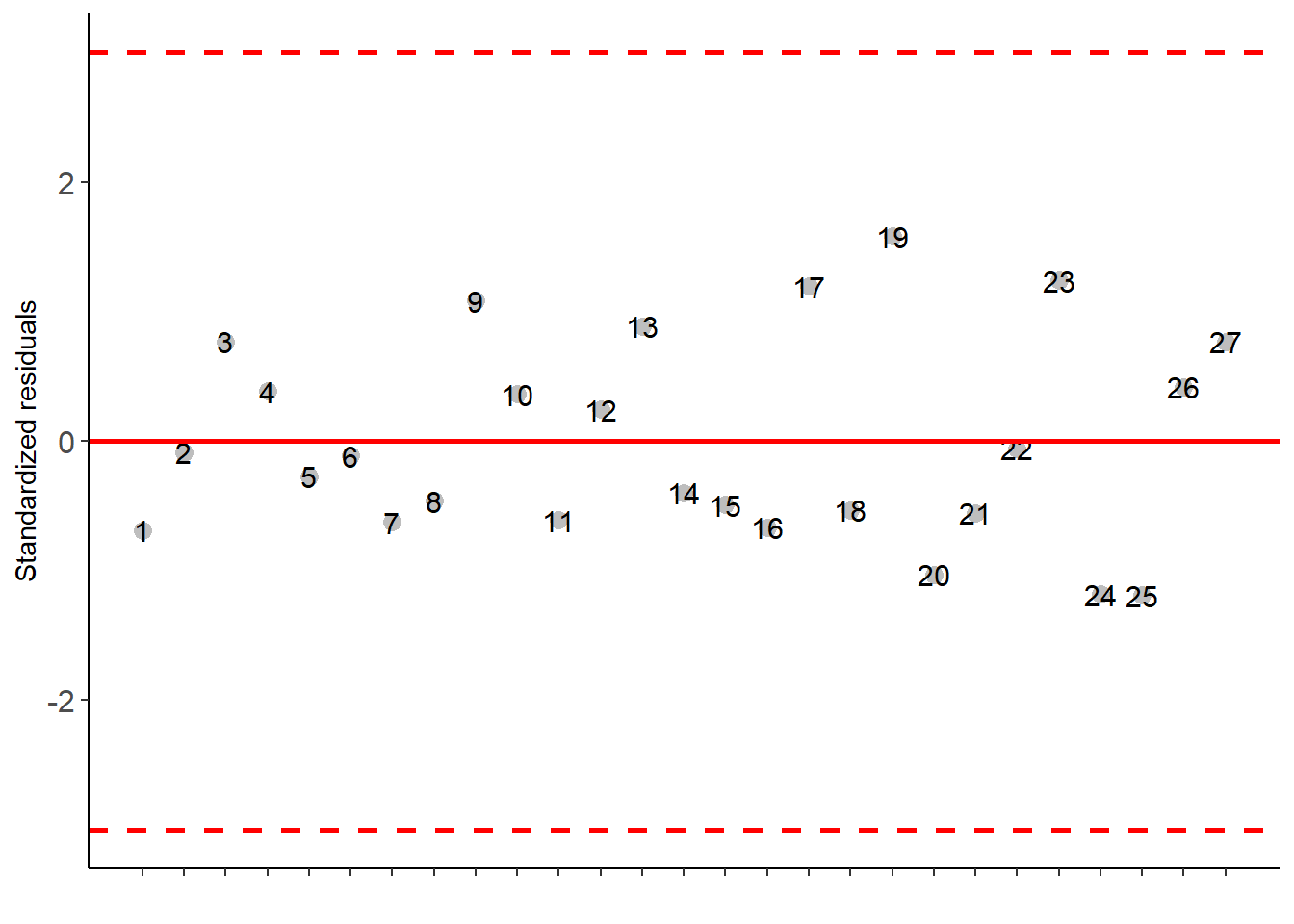
##
## -----------------------------------------------------------------
## Multiple Comparison Test
## -----------------------------------------------------------------
## resp groups
## Country orange 250.3333 a
## NRL 193.3333 b
## FRL 192.3333 b
## Cleópatra 183.6667 bc
## Clove Lemon 182.3333 bc
## Clove Tangerine 180.3333 bc
## Citranger-troyer 165.3333 bc
## Sunki 155.3333 bc
## Trifoliata 140.0000 c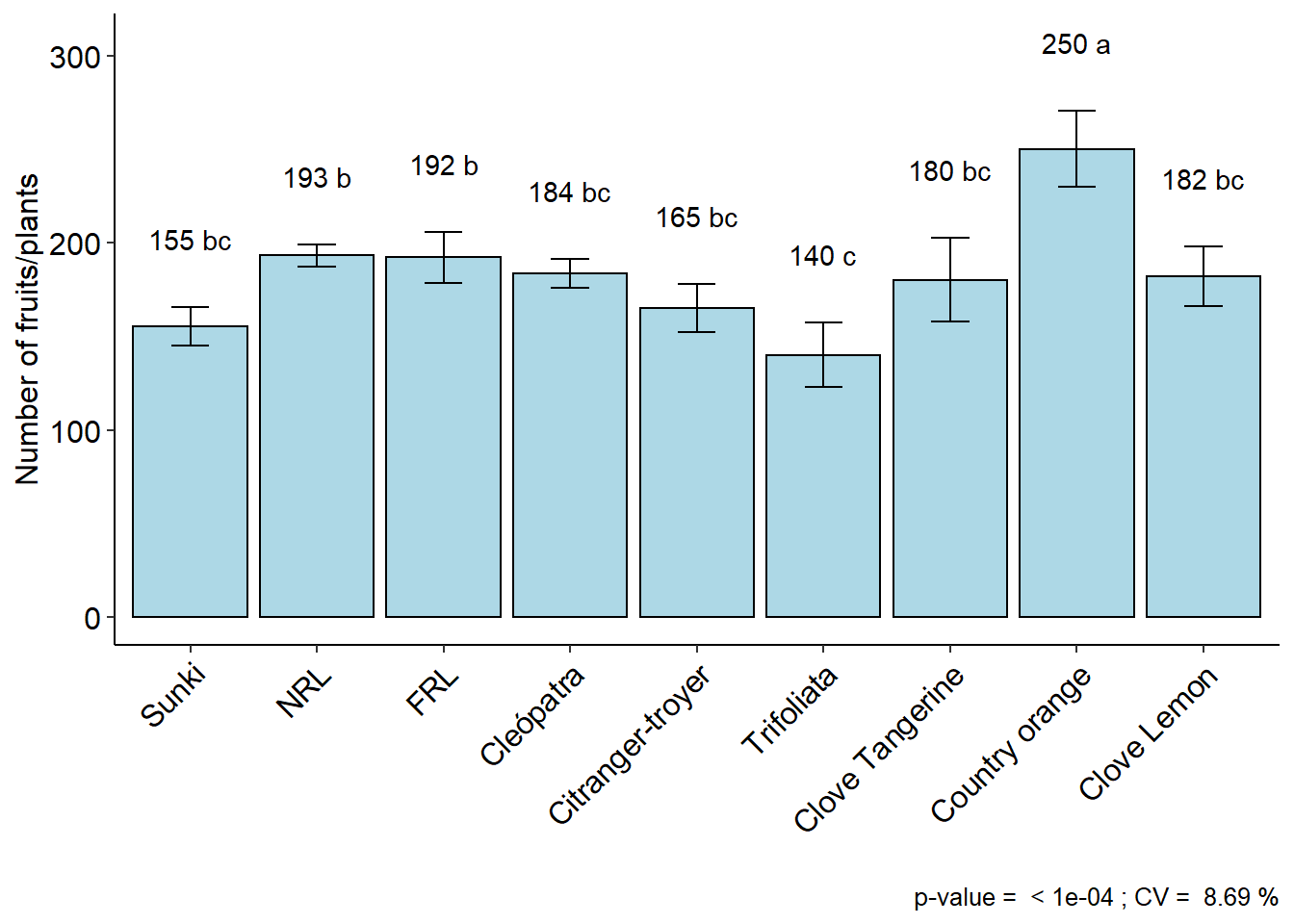
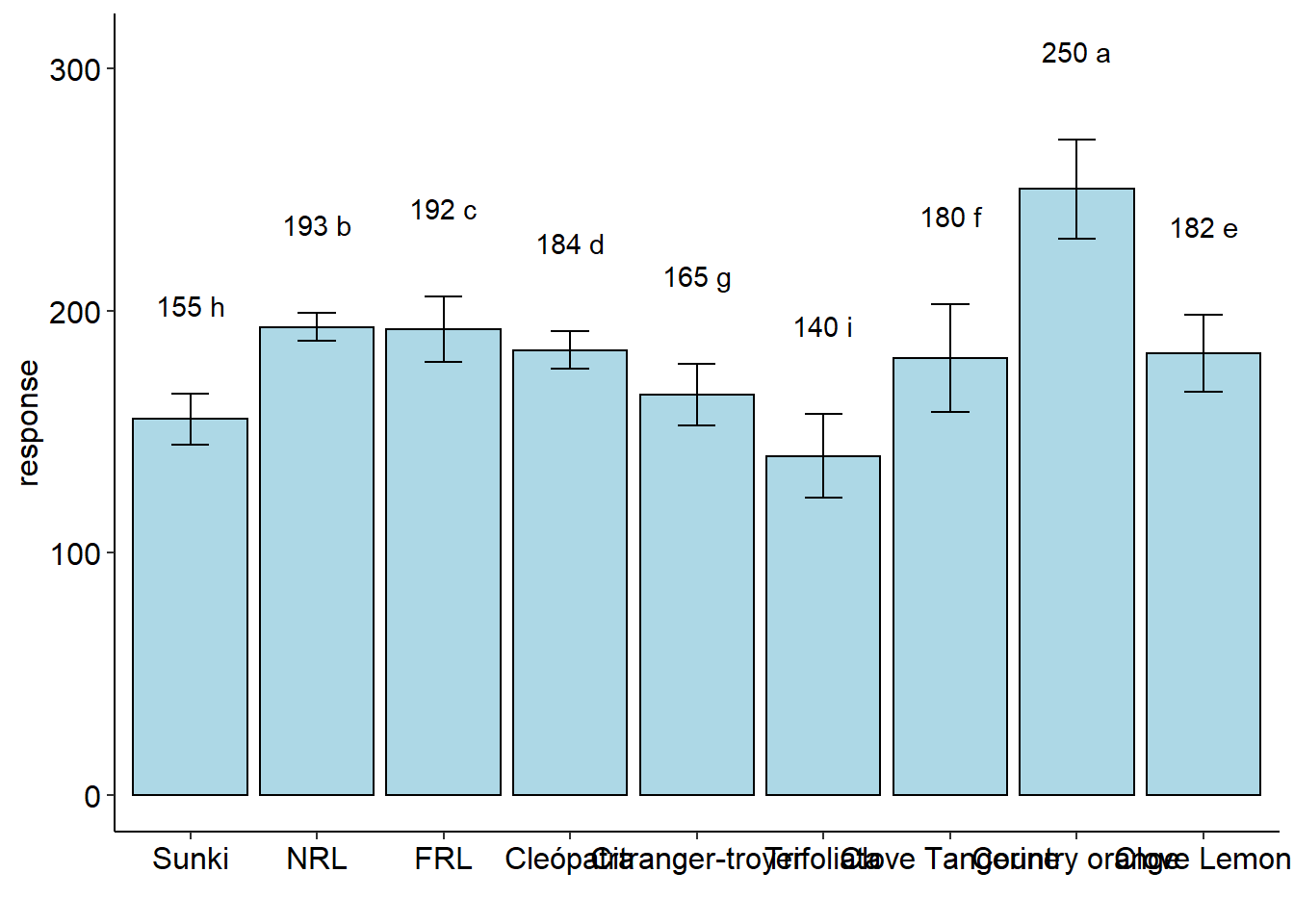
7.3 Teste de Friedman
with(laranja, DBC(trat, bloco, resp, test="noparametric"))##
##
## -----------------------------------------------------------------
## Statistics
## -----------------------------------------------------------------
## Chisq Df p.chisq F DFerror p.F t.value LSD
## 32 8 9.314161e-05 Inf 24 0 2.063899 0
##
##
## -----------------------------------------------------------------
## Parameters
## -----------------------------------------------------------------
## test name.t ntr alpha
## Friedman trat 9 0.05
##
##
## -----------------------------------------------------------------
## Multiple Comparison Test
## -----------------------------------------------------------------
## Mean SD Rank Groups
## Citranger-troyer 165.3333 12.858201 12 g
## Cleópatra 183.6667 7.767453 24 d
## Clove Lemon 182.3333 15.947832 20 e
## Clove Tangerine 180.3333 22.368132 16 f
## Country orange 250.3333 20.502032 36 a
## FRL 192.3333 13.650397 28 c
## NRL 193.3333 5.773503 32 b
## Sunki 155.3333 10.503968 8 h
## Trifoliata 140.0000 17.320508 4 i