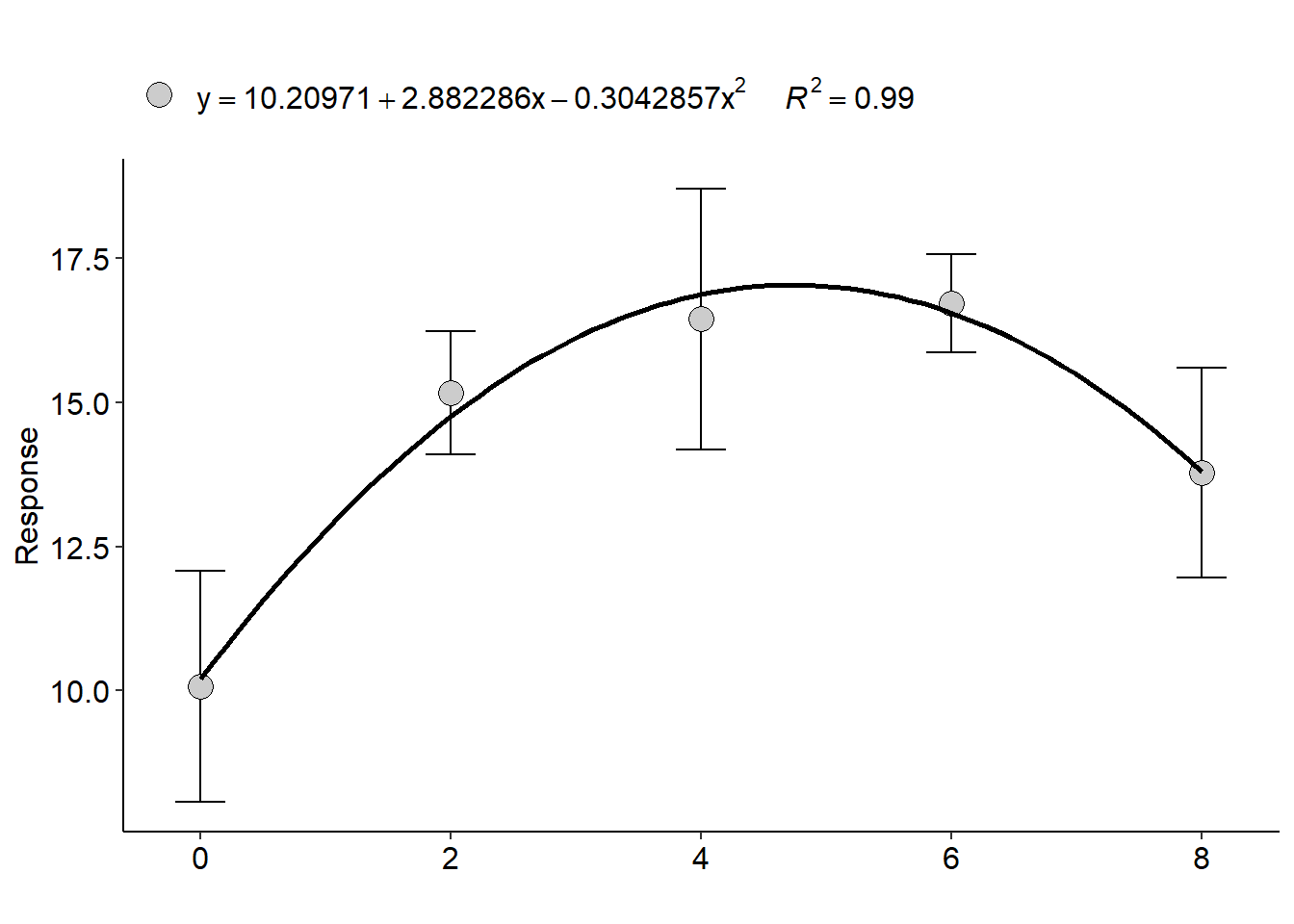6 Delineamento Inteiramente Casualizado
6.1 Teoria
O Delineamento inteiramente casualizado é considerado o delineamento mais simples dentro da estatistica. No DIC as unidades experimentais são destinadas a cada tratamento de uma forma inteiramente casual (sorteio). Os experimentos formulados com este delineamento são denominados “experimentos inteiramente ao acaso.”
O DIC apresenta as seguintes características:
- Considera apenas os princípios de repetição e casulização;
- Os tratamentos são divididos em parcelas de forma inteiramente casual;
- Exige que o material experimental seja semelhante e que as condições de estudo sejam completamentes uniformes;
- Os aspectos que devem ser considerados na semelhança entre as U.E. são aqueles que interferem nas respostas das mesmas aos tratamentos;
- Ele geralmente é mais utilizado em experimentos nos quais as condições experimentais podem ser bastante controladas (por exemplo em laboratórios);
6.1.1 Vantagens
Delineamento flexível - número de tratamentos e repetições depende apenas da quantidade de parcelas disponíveis
O número de repetições pode diferir de um tratamento para o outro (experimento não balanceado)
A análise estatística é simples
O número de G.L. resíduo é o maior possível
6.1.2 Desvantagens
Exige homogeneidade das condições ambientais
Pode estimar uma variância residual muito alta
6.1.3 Modelo matemático para DIC
\[\begin{eqnarray} y_{ji}=\mu+\tau_i+\varepsilon_{ij} \end{eqnarray}\]
\(y_{ji}\): é a observação referente ao tratamento i na repetição j;
\(\mu\): é a média geral (ou constante comum a todas as observações);
\(\tau_i\): é o efeito de tratamento, com \(i = 1, 2, . . . , I\);
\(\varepsilon_{ij}\): é o erro experimental, tal que \(\varepsilon_{ij}\)~N(0; \(\sigma^2\)).
6.1.4 Hipóteses e Modelo
\[\begin{eqnarray*} \left\{ \begin{array}{ll} H_0: & \mu_1 = \mu_2 =\mu_i\\[.2cm] H_1: & \mu_i \neq \mu_i' \qquad i \neq i'. \end{array} \right. \end{eqnarray*}\]
| CV | G.L. | S.Q. | Q.M. | Fcalc | Ftab |
|---|---|---|---|---|---|
| Tratamentos | \(a - 1\) | \(SQ_{Trat}\) | \(\frac{SQ_{Trat}}{a-1}\) | \(\frac{QMTrat}{QMRes}\) | \(F(\alpha;GL_{Trat} ;GL_{Res})\) |
| resíduo | \(a(b-1)\) | \(SQ_{Res}\) | \(SQRes\) | - | |
| Total | \(ab-1\) | \(SQ_{Total}\) | - | - |
Correção
\(C = \frac{(\sum Y_{ij})^2}{ij}\)
Soma de Quadrados Total
\(SQ_{Total}=\sum Y_{ij}^2-C\)
Soma de Quadrados Tratamento
\(SQ_{Tratamento}=\frac{1}{J}\sum Y_{i}^2-C\)
Soma de Quadrados do resíduo
\(SQ_{Resíduo} = SQ_{Total} - SQ_{Tratamento}\)
Quadrado Médio do Tratamento
\(QM_{Tratamento} = \frac{SQ_{Tratamento}}{GL_{Tratamento}}\)
Quadrado Médio do Resíduo
\(QM_{Resíduo} = \frac{SQ_{Resíduo}}{GL_{Resíduo}}\)
F calculado
\(F_{Calculado}=\frac{QM_{Tratamento}}{QM_{Resíduo}}\)
6.2 DIC
Considere o seguinte conjunto de dados:
rm(list=ls())
data(pomegranate)6.2.0.1 default
Por default, o AgroR realiza a análise de variância, teste de normalidade dos erros de Shapiro-Wilk, teste de homogeneidade das variâncias de Bartlett, teste de independência dos erros de Durbin-Watson, teste de comparação múltipla de Tukey e o gráfico de colunas.
with(pomegranate, DIC(trat, WL))##
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9448293 0.2087967## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 8.568274 0.1275737## As the calculated p-value is greater than the 5% significance level,hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 2.104821 0.1924474## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 10.84
## R-squared = 0.92
## Mean = 2.2596
## Median = 2.225
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## trat 5 3.692121 0.73842417 12.31191 2.723541e-05
## Residuals 18 1.079575 0.05997639## As the calculated p-value, it is less than the 5% significance level.The hypothesis H0 of equality of means is rejected. Therefore, at least two treatments differ##
##
## -----------------------------------------------------------------
## Multiple Comparison Test
## -----------------------------------------------------------------
## resp groups
## T5 2.6375 a
## T4 2.6200 a
## T3 2.6175 a
## T6 2.1625 ab
## T1 1.8425 b
## T2 1.6775 b## 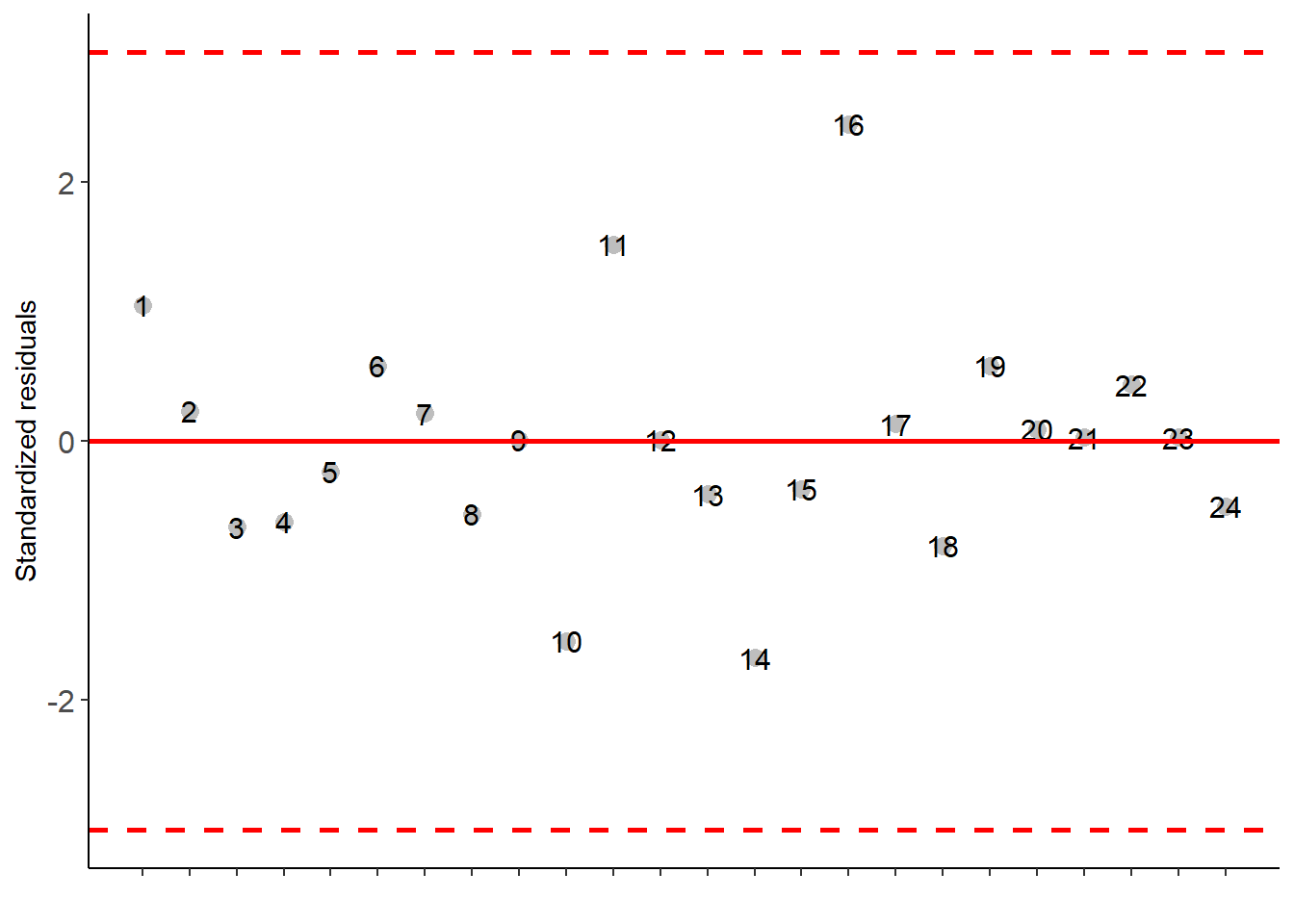
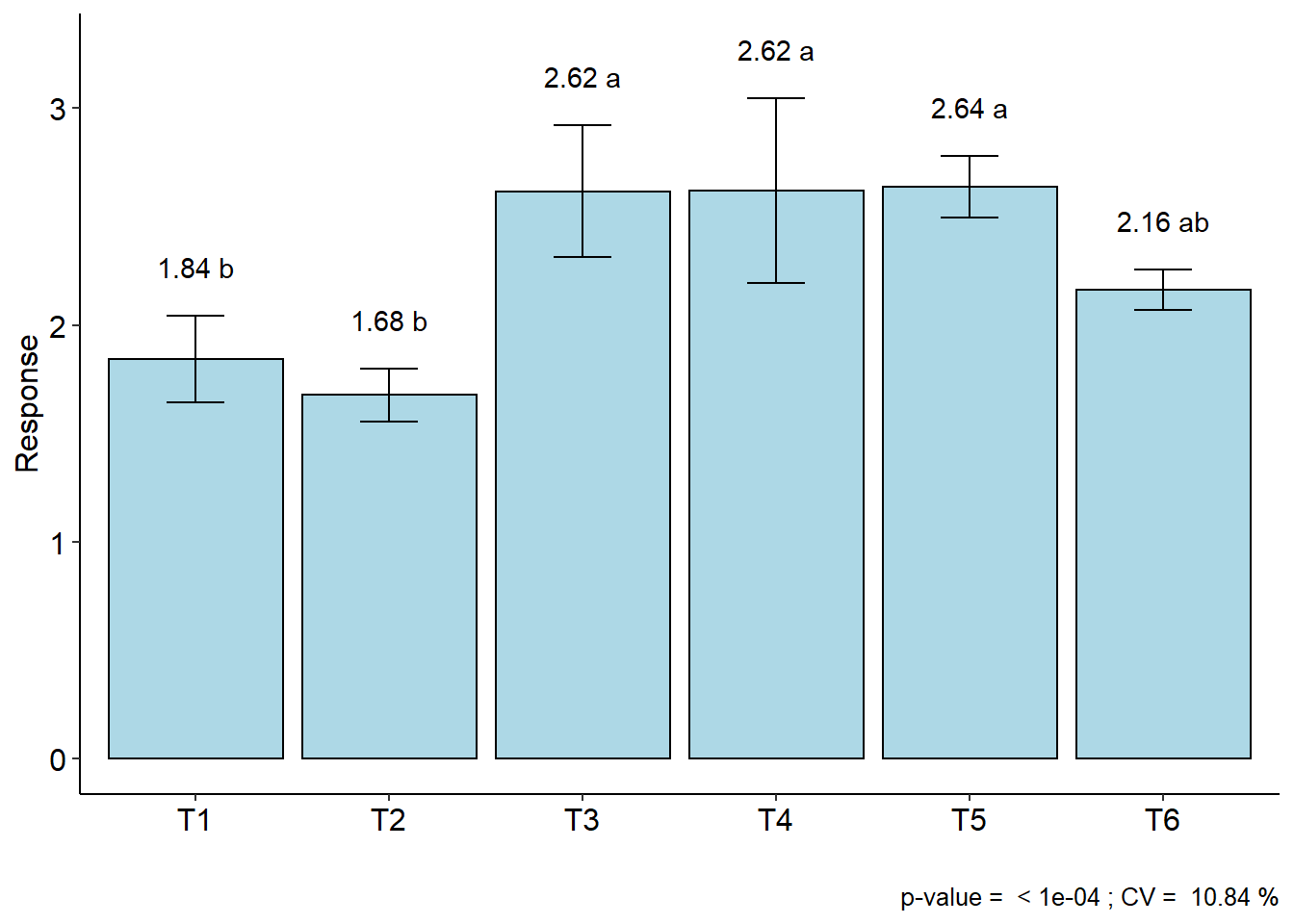
6.2.0.2 Alterando teste de médias
Para alterar o teste de médias, é necessário alterar o argumento mcomp.
with(pomegranate, DIC(trat, WL)) # tukeywith(pomegranate, DIC(trat, WL, mcomp = "sk")) # Scott-Knottwith(pomegranate, DIC(trat, WL, mcomp = "duncan")) # Duncanwith(pomegranate, DIC(trat, WL, mcomp = "lsd")) # LSD6.3 Transformando dados
- O modelo de Análise de Variância pressupõe que exista homocedasticidade, ou seja, que os tratamentos apresentem a mesma variabilidade;
- Algumas vezes este pressuposto pode não ser atendido e assim, para corrigir este problema existe uma saída por vezes bastante simples que é a transformação de dados;
- Esta técnica consiste na utilização de um artifício matemático para tornar o modelo de ANOVA válido.
6.3.0.0.1 Heterogeneidade Irregular
Ocorre quando alguns tratamentos apresentam maior variabilidade do que outros, contudo, não existe uma associação entre média e variância;
Neste caso, não há uma transformação matemática que elimine esta variabilidade.
Solução:
Modelos Lineares Generalizados;
Análise não paramétrica.
6.3.0.0.2 Heterogeneidade Regular
- Acontece quando existe alguma associação entre as médias dos tratamentos e a variância;
- A heterocedasticidade regular está associada é falta de normalidade do erros;
Solução:
Transformação dos dados;
Modelos Lineares Generalizados;
Análise não paramétrica.
6.3.0.0.3 Princípio de transformação
Seja \(E(Y) = \mu\) a média de Y e suponha que o desvio padrão de Y é proporcional a potência da média de Y tal que:
\(\sigma Y \alpha \mu^\alpha.\)
O objetivo é encontrar uma transformação de \(Y\) que gere uma variância constante.
Suponha que a transformação é uma potência dos dados originais, isto é:
\(Y^*=Y^\lambda\)
Assim, pode ser mostrado que:
\(\sigma Y^* \alpha \mu^{\lambda+ \alpha-1}.\)
Caso \(\lambda = 1-\alpha\), então a variância dos dados transformados \(Y^*\) é constante, mostrando que não é necessário transformação.
Algumas das transformações mais comuns são:
| \(\lambda\) | Transformação |
|---|---|
| 1 | Nenhuma |
| 0,5 | \(\sqrt{y}\) |
| 0 | log(y) |
| -0,5 | \(\frac{1}{\sqrt{y}}\) |
| -1 | \(\frac{1}{y}\) |
Box & Cox (1964) mostraram como o parâmetro de transformação \(\lambda\) em \(Y^* = Y^\lambda\) pode ser estimado simultaneamente com outros parâmetros do modelo (média geral e efeitos de tratamentos) usando o método de máxima verossimilhança. O procedimento consiste em realizar, para vários valores de \(\lambda\), uma análise de variância padrão sobre:
\[Y_i(\lambda) = \left\{ \begin{array}{ll} \ln(X_i),~~~~~~\textrm{se $\lambda = 0$,} \\ \\ \dfrac{X_i^{\lambda} - 1}{\lambda},~~~~\textrm{se $\lambda \neq 0$,}\end{array} \right.\]
A estimativa de máxima verossimilhança de \(\lambda\) é o valor para o qual a soma de quadrado do resíduo, SQRes(\(\lambda\)), é mínima.
Este valor de \(\lambda\) é encontrado através do gráfico de SQRes(\(\lambda\)) versus \(\lambda\), sendo que \(\lambda\) é o valor que minimiza a SQRes(\(\lambda\)).
Ou, ainda, o valor de \(\lambda\) que maximiza a função de logverossimilhança.
Um intervalo de confiança \(100(1-\alpha)\)% para \(\lambda\) pode ser encontrado calculando-se:
\(IC(\lambda) = SQRes(\lambda)(1 \pm \frac{t2^2/2=2;v }{v})\)
em que \(v\) é o número de graus de liberdade.
Se o intervalo de confiança incluir o valor \(\lambda = 1\), isto quer dizer que não é necessário transformar os dados.
No pacote AgroR, o argumento transf define a transformação solicitada, conforme a seguir:
with(pomegranate, DIC(trat, WL, transf = 0))##
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9694183 0.6526381## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 5.657984 0.3409331## As the calculated p-value is greater than the 5% significance level,hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 2.001907 0.1261966## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 12.59
## R-squared = 0.94
## Mean = 2.2596
## Median = 2.225
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## trat 5 0.7834427 0.15668854 15.61523 5.318727e-06
## Residuals 18 0.1806181 0.01003434## As the calculated p-value, it is less than the 5% significance level.The hypothesis H0 of equality of means is rejected. Therefore, at least two treatments differ##
##
## -----------------------------------------------------------------
## Multiple Comparison Test
## -----------------------------------------------------------------
## resp groups respO
## T5 0.9687134 a 2.6375
## T3 0.9570245 a 2.6175
## T4 0.9537130 a 2.6200
## T6 0.7705460 ab 2.1625
## T1 0.6068284 bc 1.8425
## T2 0.5152916 c 1.6775##
## NOTE: resp = transformed means; respO = averages without transforming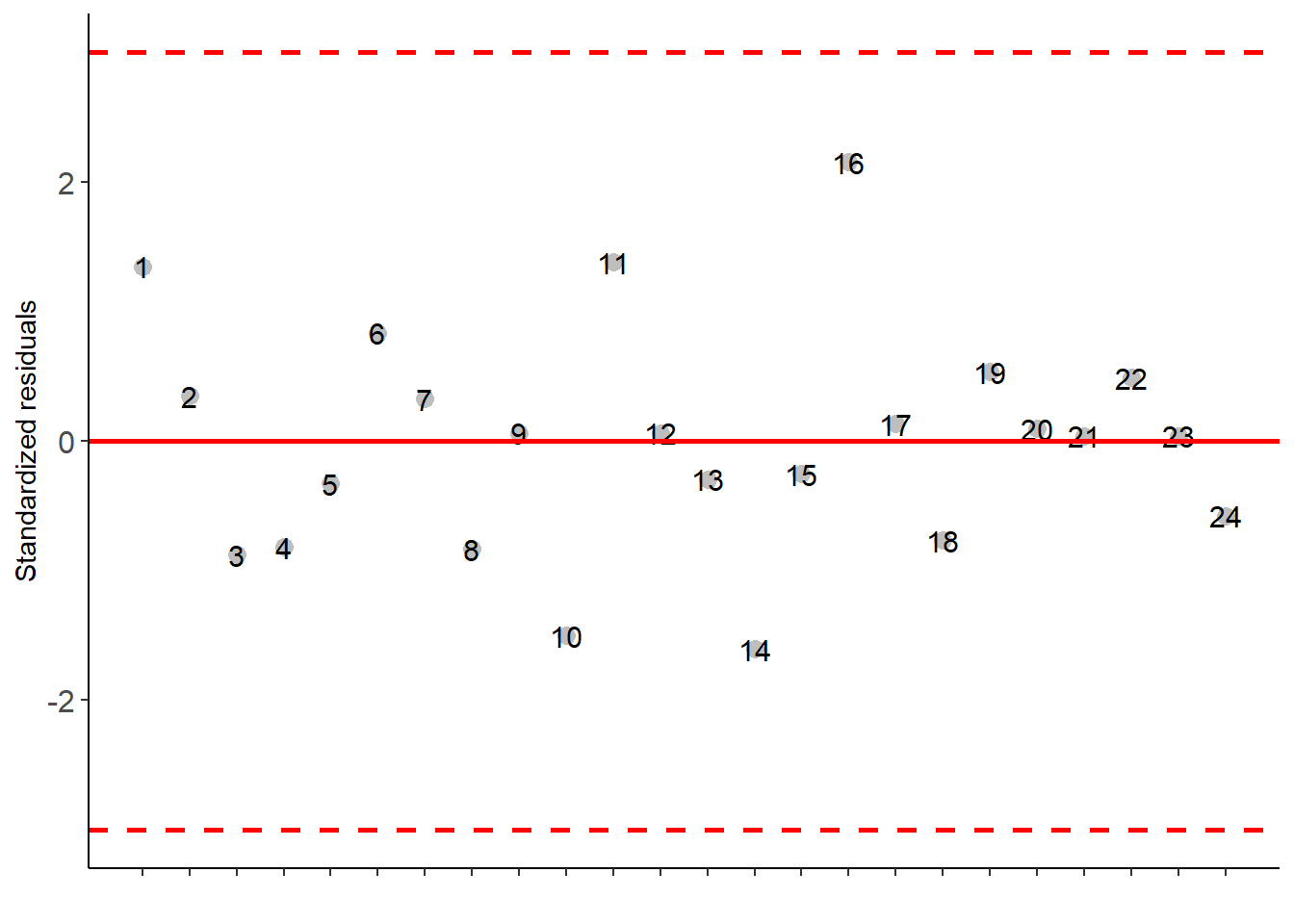
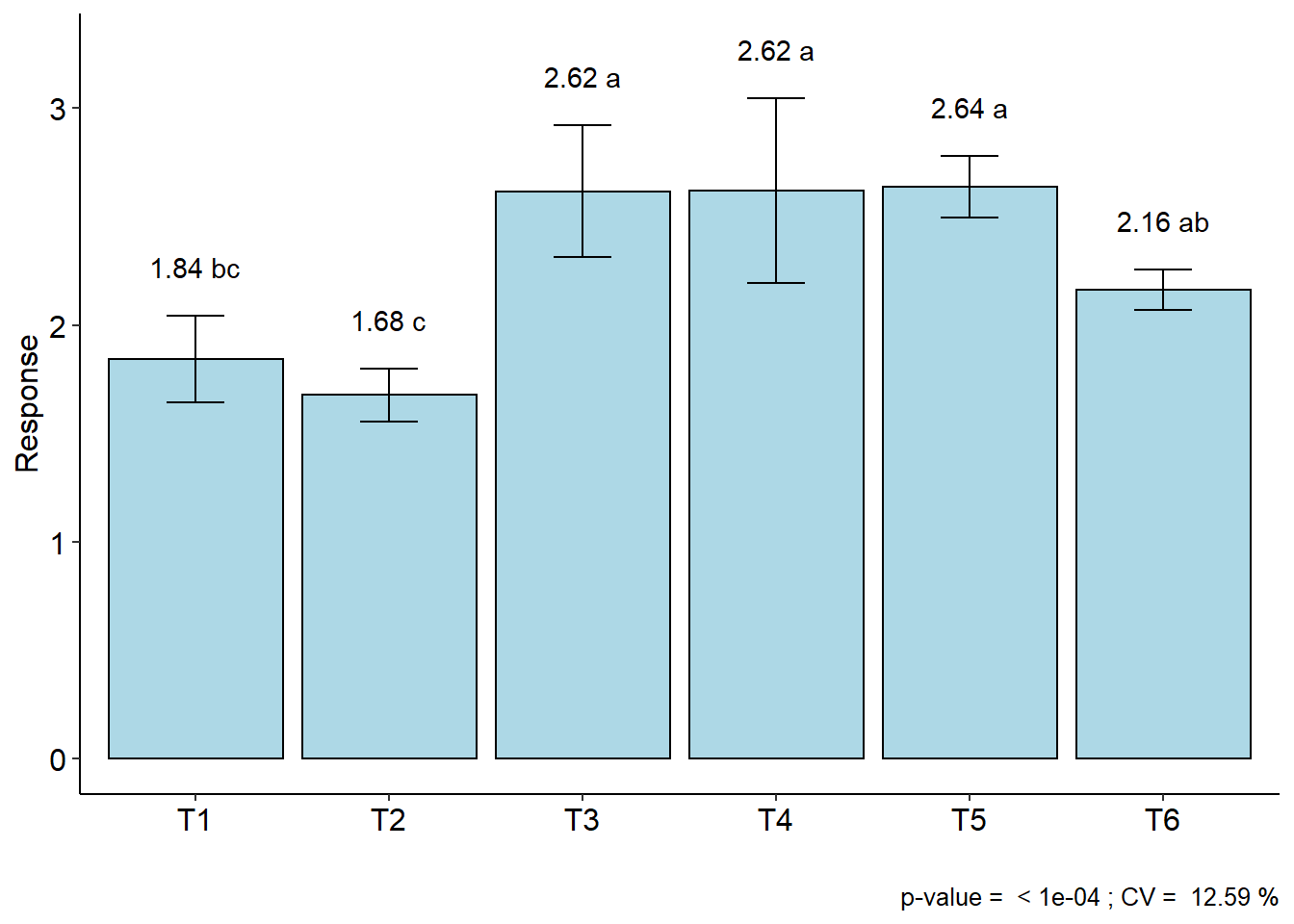
6.4 Kruskal-Wallis
with(pomegranate, DIC(trat, WL, test = "noparametric", geom="point"))##
##
## -----------------------------------------------------------------
## Statistics
## -----------------------------------------------------------------
## Chisq p.chisq
## 18.75631 0.002133687
##
##
## -----------------------------------------------------------------
## Parameters
## -----------------------------------------------------------------
## test p.ajusted name.t ntr alpha
## Kruskal-Wallis holm trat 6 0.05
##
##
## -----------------------------------------------------------------
## Multiple Comparison Test
## -----------------------------------------------------------------
## Mean SD Rank Groups
## T1 1.8425 0.19939492 5.75 c
## T2 1.6775 0.12284814 3.50 c
## T3 2.6175 0.30619983 18.25 ab
## T4 2.6200 0.42669271 17.25 ab
## T5 2.6375 0.14244882 19.50 a
## T6 2.1625 0.09429563 10.75 bc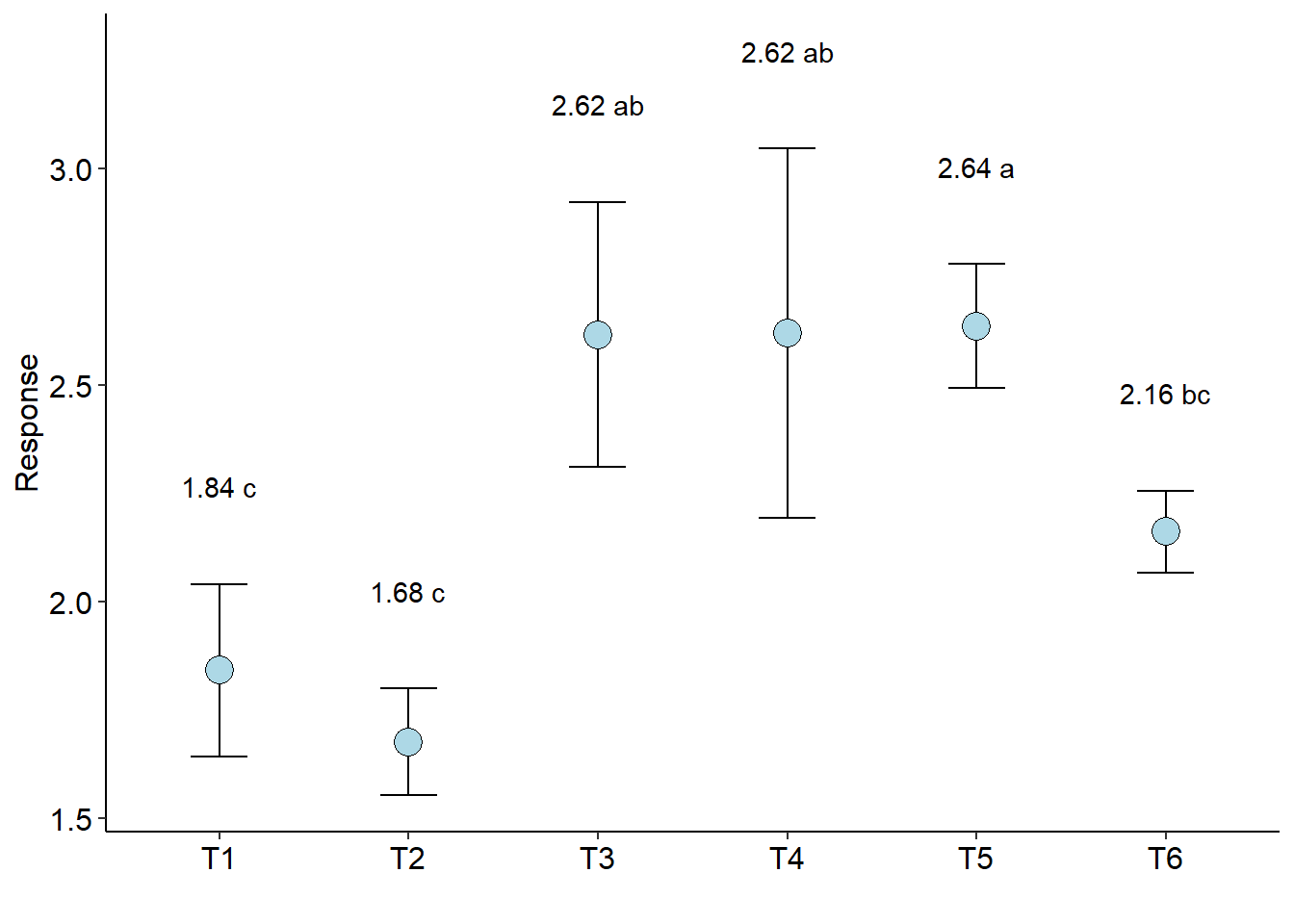
6.4.0.1 Alterando parâmetros gráficos
with(pomegranate, DIC(trat, WL, geom="point")) # tipo de gráficowith(pomegranate, DIC(trat, WL,
ylab = "Weight loss (%)",
xlab="Treatments")) # nome de eixos6.5 Fator Quantitativo
rm(list=ls())
data("phao")
with(phao, DIC(dose,comp,quali=FALSE,grau=2))##
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9647717 0.5174008## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 4.428915 0.3510598## As the calculated p-value is greater than the 5% significance level,hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 1.801827 0.08064338## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 11.71
## R-squared = 0.93
## Mean = 14.436
## Median = 15.3
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## trat 4 145.8096 36.4524 12.76166 2.557884e-05
## Residuals 20 57.1280 2.8564## As the calculated p-value, it is less than the 5% significance level.The hypothesis H0 of equality of means is rejected. Therefore, at least two treatments differ
##
##
## -----------------------------------------------------------------
## Regression
## -----------------------------------------------------------------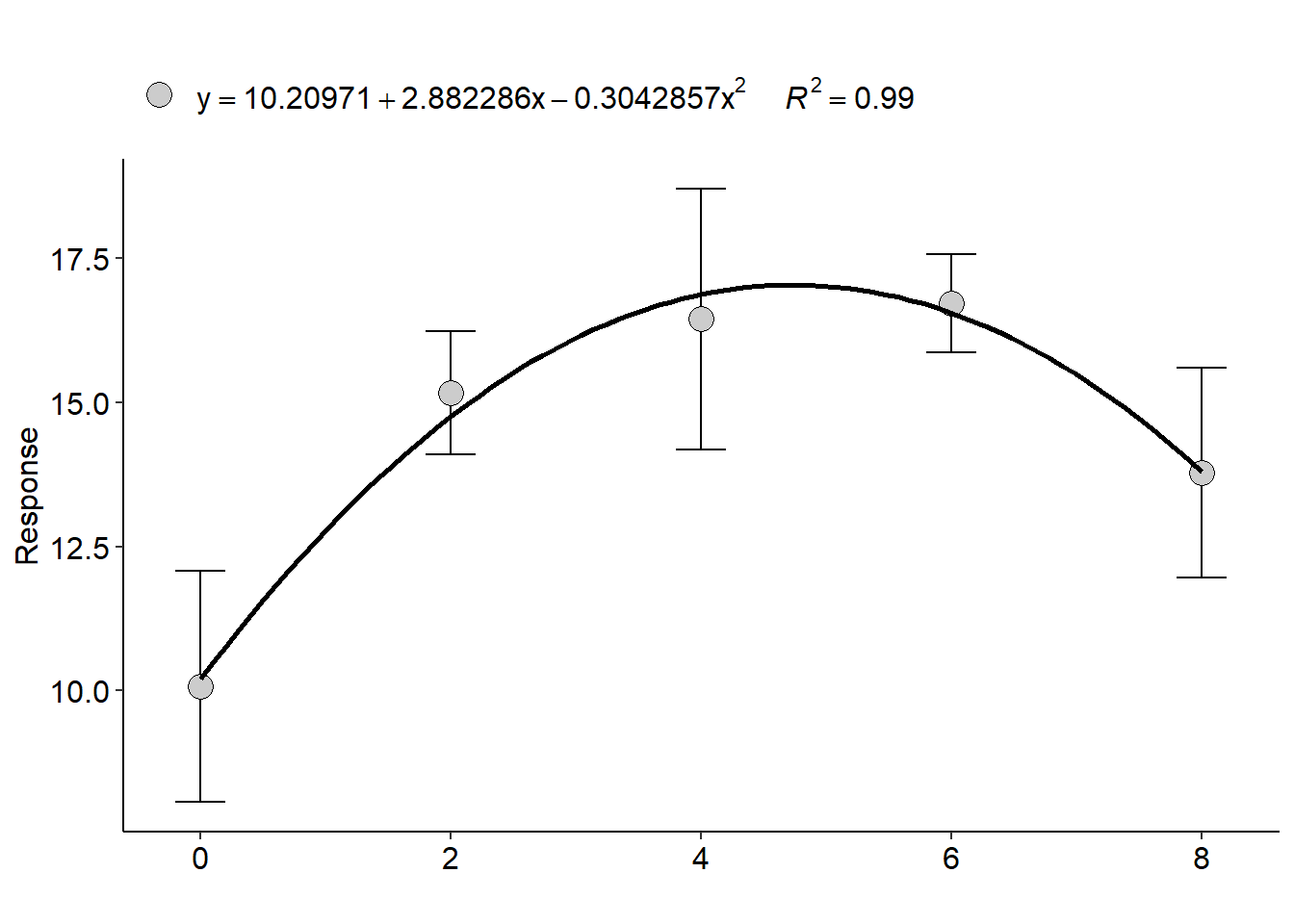
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.2097143 0.68981140 14.800733 6.427099e-13
## trat 2.8822857 0.40856781 7.054608 4.456995e-07
## I(trat^2) -0.3042857 0.04897332 -6.213296 2.971498e-06
##
## ----------------------------------------------------
## Deviations from regression
## ----------------------------------------------------
## GL SQ F p-value
## 2 1.968229 0.3445296 0.7126767