11 Esquema fatoria duplo
11.1 Teoria
Nos experimentos mais simples comparamos níveis (tratamentos) de apenas um fator; Entretanto, existem casos em que dois ou mais fatores devem ser estudados simultaneamente para que possam nos conduzir a resultados de interesse;
Em geral, os experimentos fatoriais são mais eficientes para este tipo de experimento, pois estudam, ao mesmo tempo, os efeitos de dois ou mais fatores, cada um deles com dois ou mais níveis.
O fatorial é um tipo de esquema, ou seja, uma das maneiras de organizar os tratamentos e não um tipo de delineamento;
Os experimentos fatoriais são montados segundo um tipo de delineamento experimental;
Nos experimentos fatoriais, os tratamentos são obtidos pelas combinações dos níveis dos fatores.
11.1.1 Tipos de efeitos avaliados
Efeito Principal: é o efeito de cada fator, independente do efeito dos outros fatores;
Efeito de Interação: é o efeito simultâneo dos fatores sobre a variável em estudo. Dizemos que ocorre interação entre os fatores quando os efeitos dos níveis de um fator são modificados pelos níveis do outro fator.
11.1.2 Vantagens
Pode-se estudar dois ou mais fatores num único experimento.
Pode-se, por meio dos efeitos das interações, verificar se um fator é independente ou dependente do(s) outro(s).
11.1.3 Desvantagens
O número de tratamentos ou combinações de níveis de fatores cresce, rapidamente, com o aumento do número de níveis, em cada fator, ou mesmo com o aumento do número de fatores.
A interpretação dos resultados se torna mais difícil é medida que aumentamos o número de níveis e de fatores no experimento.
11.1.4 Modelo estatístico
As observações podem ser descritas pelo modelo estatístico linear:
\(y_{ij} = \mu+\tau_{i}+\beta_{j}+(\tau\beta)_{ij}+\epsilon_{ij}\)
- i = 1; 2; : : : ; a
- j = 1; 2; : : : ; b
- k = 1; 2; : : : ; r
em que:
- \(y_{ijk}\) é o valor observado no i-ésimo nivel do Fator A e j-ésima nível do Fator B;
- \(\mu\) é uma constante;
- \(\tau_{i}\) é o efeito do i-ésimo nível do fator A;
- \(\beta_{j}\) é o efeito do j-ésimo nível do fator B;
- \((\tau\beta)_ij\) é o efeito da interação entre \(\tau_{i}\) e \(\beta_{j}\);
- \((\epsilon)ijk\) é o componente de erro aleatório.
11.1.5 Hipóteses e quadro da análise de variância
No experimento fatorial com 2 fatores, deseja-se testar a signicância de ambos os fatores.
Há interesse em testar hipóteses sobre a igualdade dos efeitos do fator A, isto é:
- H0 : \(\beta_{11}\) = \(\beta_{12}\) = : : : \(\beta_{1a}\) = 0
- H1 : Pelo menos um \(\beta_{1i} \neq 0\)
e a igualdade nos efeitos do fator B, ou seja:
- H0 : \(\beta_{21}\) = \(\beta_{22}\) = : : : \(\beta_{2b}\) = 0
- H1 : Pelo menos um \(\beta_{2j} \neq 0\)
e, ainda, se há interação entre os fatores:
- H0 : \((\beta_1\beta_2)_{ij}\) = 0 para todo i ; j
- H1 : Pelo menos um \((\beta_1\beta_2)_{ij} \neq 0\)
| CV | G.L. | S.Q. | Q.M. | Fcalc |
|---|---|---|---|---|
| Fator A | \(a - 1\) | \(SQ_{A}\) | \(\frac{SQ_{A}}{a-1}\) | \(\frac{QM_{A}}{QM_{Res}}\) |
| Fator B | \(b-1\) | \(SQ_{B}\) | \(\frac{SQ_{B}}{b-1}\) | \(\frac{QM_{B}}{QM_{Res}}\) |
| Interação A x B | \((a-1)(b-1)\) | \(SQ_{AxB}\) | \(\frac{SQ_{AxB}}{(a-1)(b-1)}\) | \(\frac{QM_{AxB}}{QM_{Res}}\) |
| resíduo | \(ab(n-1)\) | \(SQ_{Res}\) | \(\frac{SQ_{Res(b)}}{ab(n-1)}\) | |
| Total | \(abn-1\) | \(SQ_{Total}\) | - |
11.2 FAT2DIC
data(cloro)
with(cloro,
FAT2DIC(f1, f2, resp, ylab="Number of nodules", legend = "Stages"))##
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9680878 0.3125183## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 9.875441 0.1957427## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 2.092504 0.1892105## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 29.83
## Mean = 218.35
## Median = 185
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## Fator1 1 16160.4 16160.4 3.810516 5.972867e-02
## Fator2 3 116554.5 38851.5 9.160929 1.596453e-04
## Fator1:Fator2 3 452096.2 150698.7 35.533773 2.663131e-10
## Residuals 32 135712.0 4241.0## 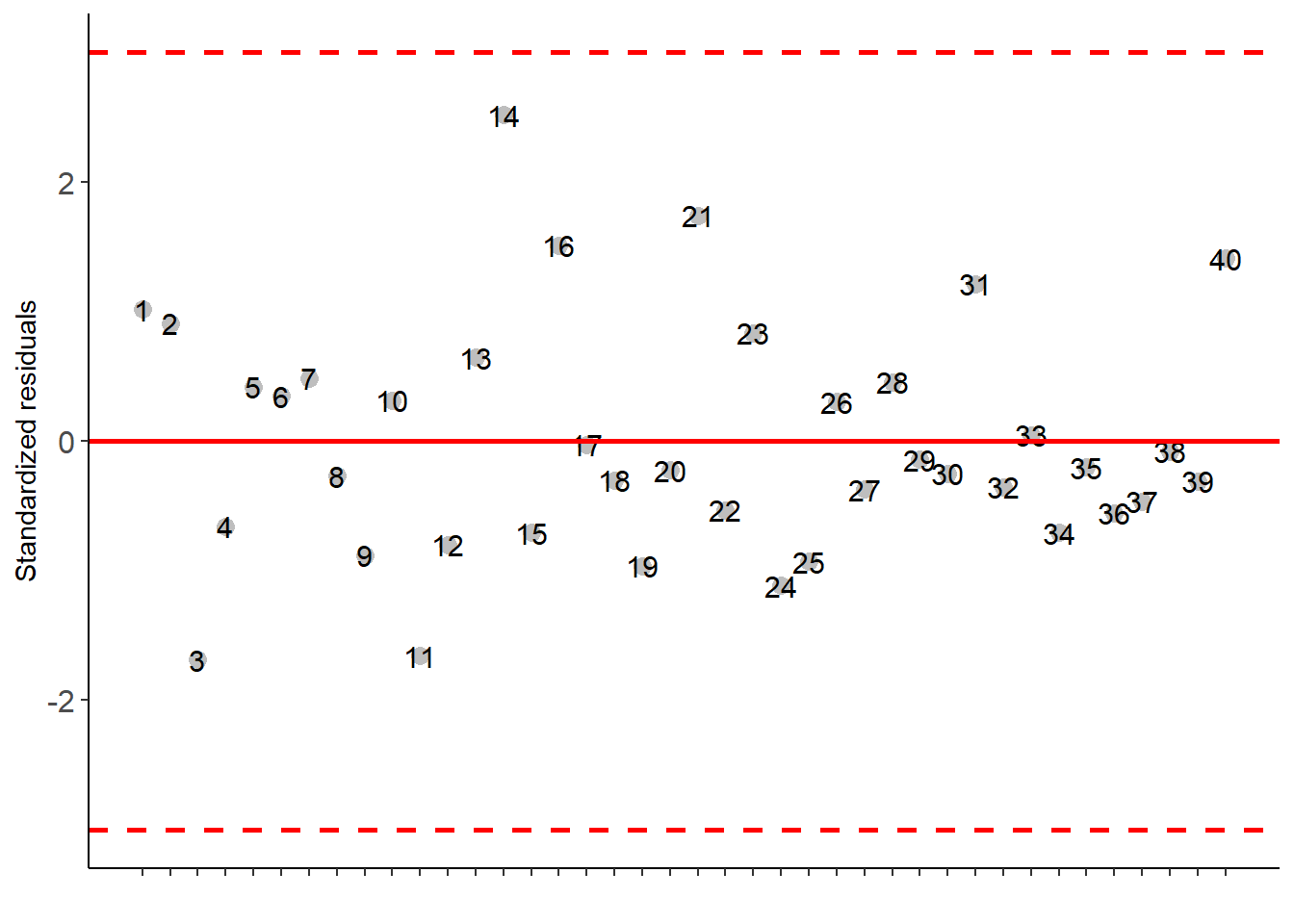
## -----------------------------------------------------------------
## Significant interaction: analyzing the interaction
## -----------------------------------------------------------------
##
## -----------------------------------------------------------------
## Analyzing F1 inside of each level of F2
## -----------------------------------------------------------------
##
## Df Sum Sq Mean Sq F value Pr(>F)
## Fator2 3 116555 38852 9.1609 0.0001596 ***
## Fator2:Fator1 4 468257 117064 27.6030 5.661e-10 ***
## Fator2:Fator1: Plantio 1 26112 26112 6.1571 0.0185315 *
## Fator2:Fator1: V1+15 1 258888 258888 61.0441 6.522e-09 ***
## Fator2:Fator1: V3+15 1 112360 112360 26.4938 1.295e-05 ***
## Fator2:Fator1: R1+15 1 70896 70896 16.7169 0.0002728 ***
## Residuals 32 135712 4241
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## -----------------------------------------------------------------
## Analyzing F2 inside of the level of F1
## -----------------------------------------------------------------
##
## Df Sum Sq Mean Sq F value Pr(>F)
## Fator1 1 16160 16160 3.8105 0.059729 .
## Fator1:Fator2 6 568651 94775 22.3474 3.699e-10 ***
## Fator1:Fator2: IN 3 75470 25157 5.9318 0.002454 **
## Fator1:Fator2: NI 3 493181 164394 38.7629 9.117e-11 ***
## Residuals 32 135712 4241
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## -----------------------------------------------------------------
## Final table
## -----------------------------------------------------------------
## Plantio V1+15 V3+15 R1+15
## IN 272.8 aA 140.4 bB 304.0 aA 236.6 aAB
## NI 170.6 bB 462.2 aA 92.0 bB 68.2 bB##
##
## Averages followed by the same lowercase letter in the column and
## uppercase in the row do not differ by the tukey (p< 0.05 )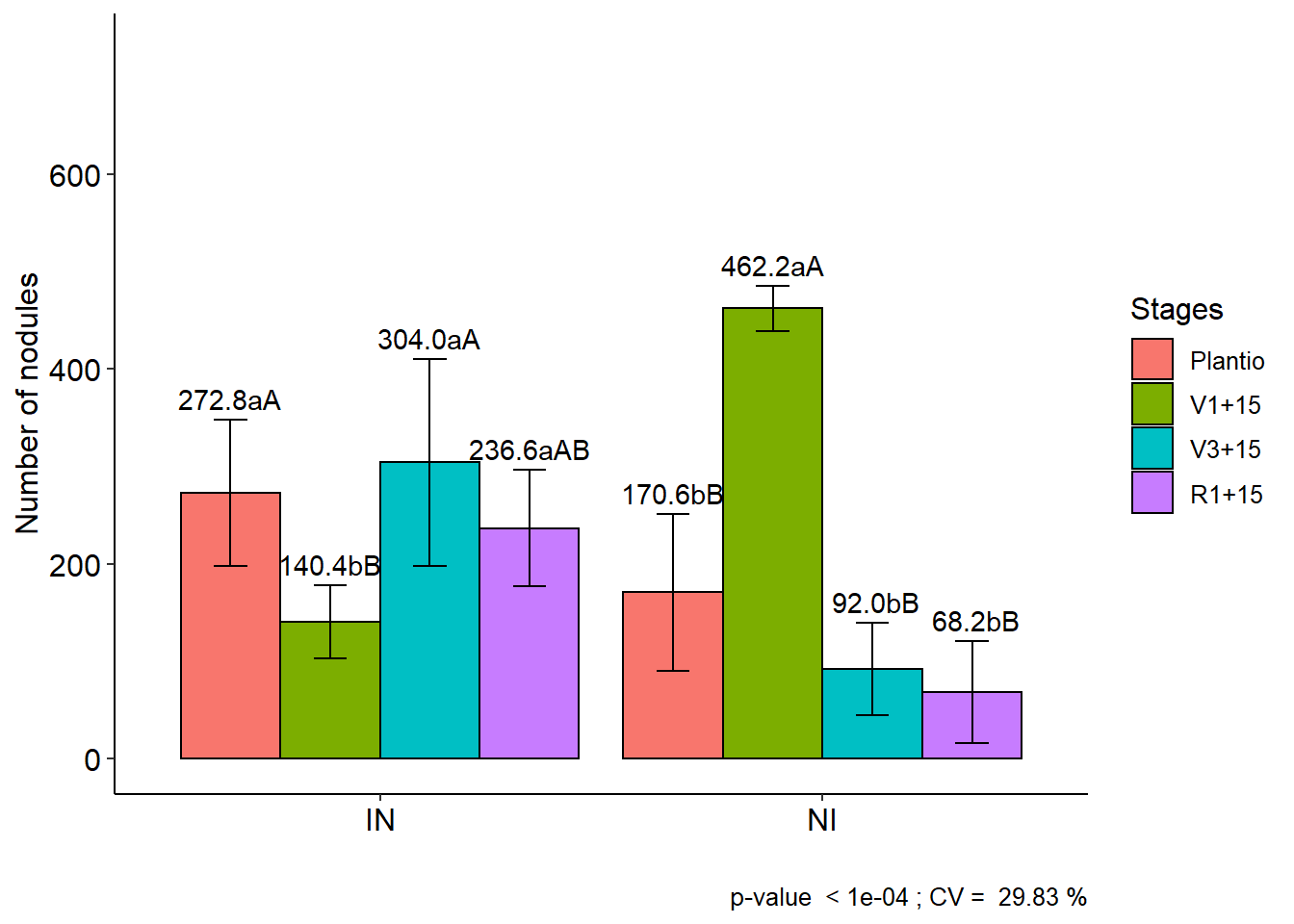
11.3 FAT2DBC
data(cloro)
with(cloro,
FAT2DBC(f1, f2, bloco, resp, ylab="Number of nodules", legend = "Stages"))##
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9548911 0.1117923## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 16.11086 0.02412261## As the calculated p-value is less than the 5% significance level, H0 is rejected. Therefore, the variances are not homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 2.047899 0.1769663## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 30.49
## Mean = 218.35
## Median = 185
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## Fator1 1 16160.4 16160.400 3.6462291 6.649143e-02
## Fator2 3 116554.5 38851.500 8.7659631 2.933552e-04
## bloco 4 11613.6 2903.400 0.6550866 6.282168e-01
## Fator1:Fator2 3 452096.2 150698.733 34.0017642 1.790168e-09
## Residuals 28 124098.4 4432.086##
## Your analysis is not valid, suggests using a non-parametric test and try to transform the data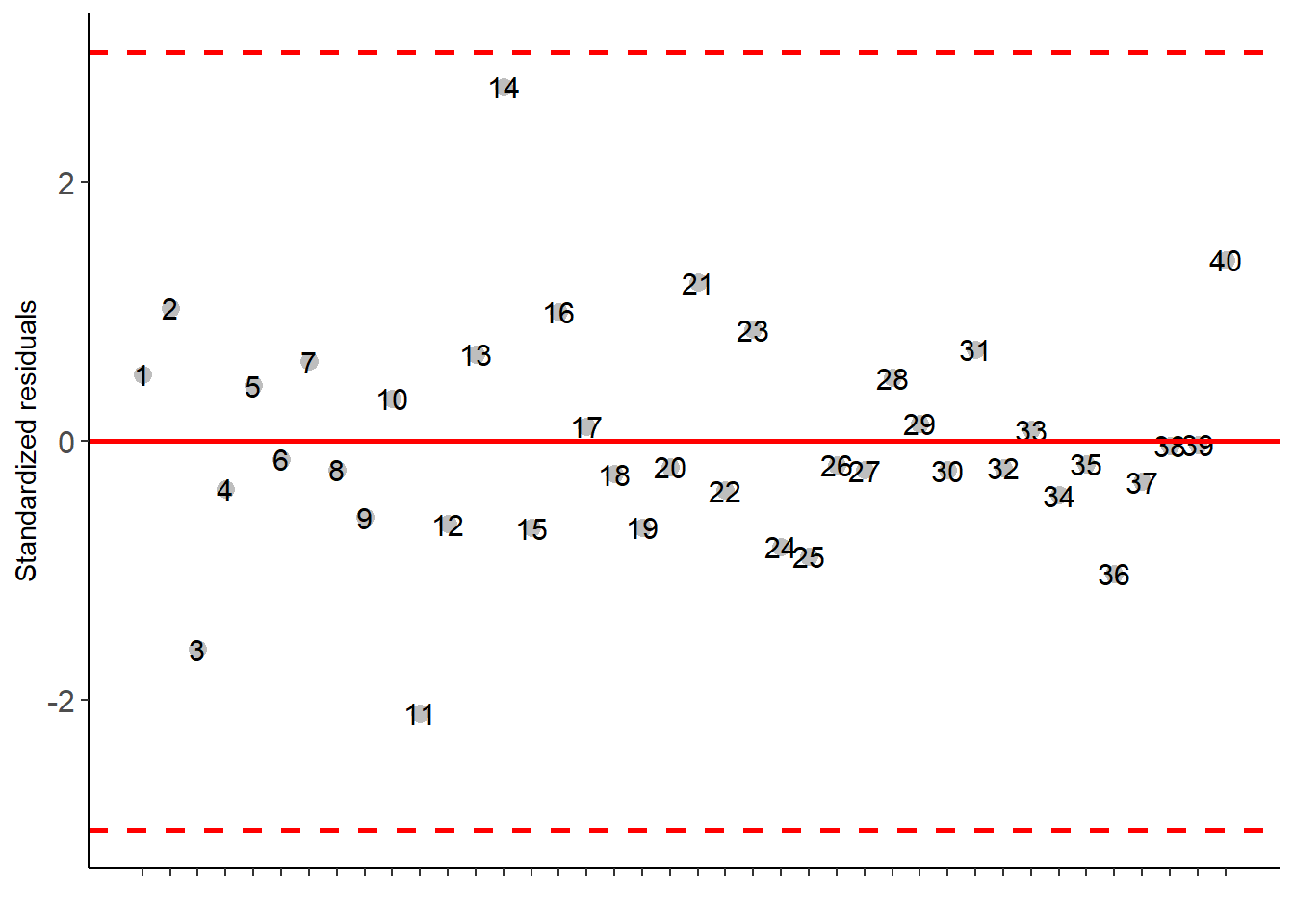
## -----------------------------------------------------------------
##
## Significant interaction: analyzing the interaction
##
## -----------------------------------------------------------------
##
## -----------------------------------------------------------------
## Analyzing F1 inside of each level of F2
## -----------------------------------------------------------------
## Df Sum Sq Mean Sq F value Pr(>F)
## bloco 4 11614 2903 0.6551 0.6282168
## Fator2 3 116555 38852 8.7660 0.0002934 ***
## Fator2:Fator1 4 468257 117064 26.4129 3.786e-09 ***
## Fator2:Fator1: Plantio 1 26112 26112 5.8916 0.0218981 *
## Fator2:Fator1: V1+15 1 258888 258888 58.4123 2.518e-08 ***
## Fator2:Fator1: V3+15 1 112360 112360 25.3515 2.520e-05 ***
## Fator2:Fator1: R1+15 1 70896 70896 15.9962 0.0004207 ***
## Residuals 28 124098 4432
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## -----------------------------------------------------------------
## Analyzing F2 inside of the level of F1
## -----------------------------------------------------------------
##
## Df Sum Sq Mean Sq F value Pr(>F)
## bloco 4 11614 2903 0.6551 0.628217
## Fator1 1 16160 16160 3.6462 0.066491 .
## Fator1:Fator2 6 568651 94775 21.3839 2.917e-09 ***
## Fator1:Fator2: IN 3 75470 25157 5.6760 0.003625 **
## Fator1:Fator2: NI 3 493181 164394 37.0917 6.882e-10 ***
## Residuals 28 124098 4432
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## -----------------------------------------------------------------
## Final table
## -----------------------------------------------------------------
## Plantio V1+15 V3+15 R1+15
## IN 272.8 aA 140.4 bB 304.0 aA 236.6 aAB
## NI 170.6 bB 462.2 aA 92.0 bB 68.2 bB##
##
## Averages followed by the same lowercase letter in the column
## and uppercase in the row do not differ by the tukey (p< 0.05 )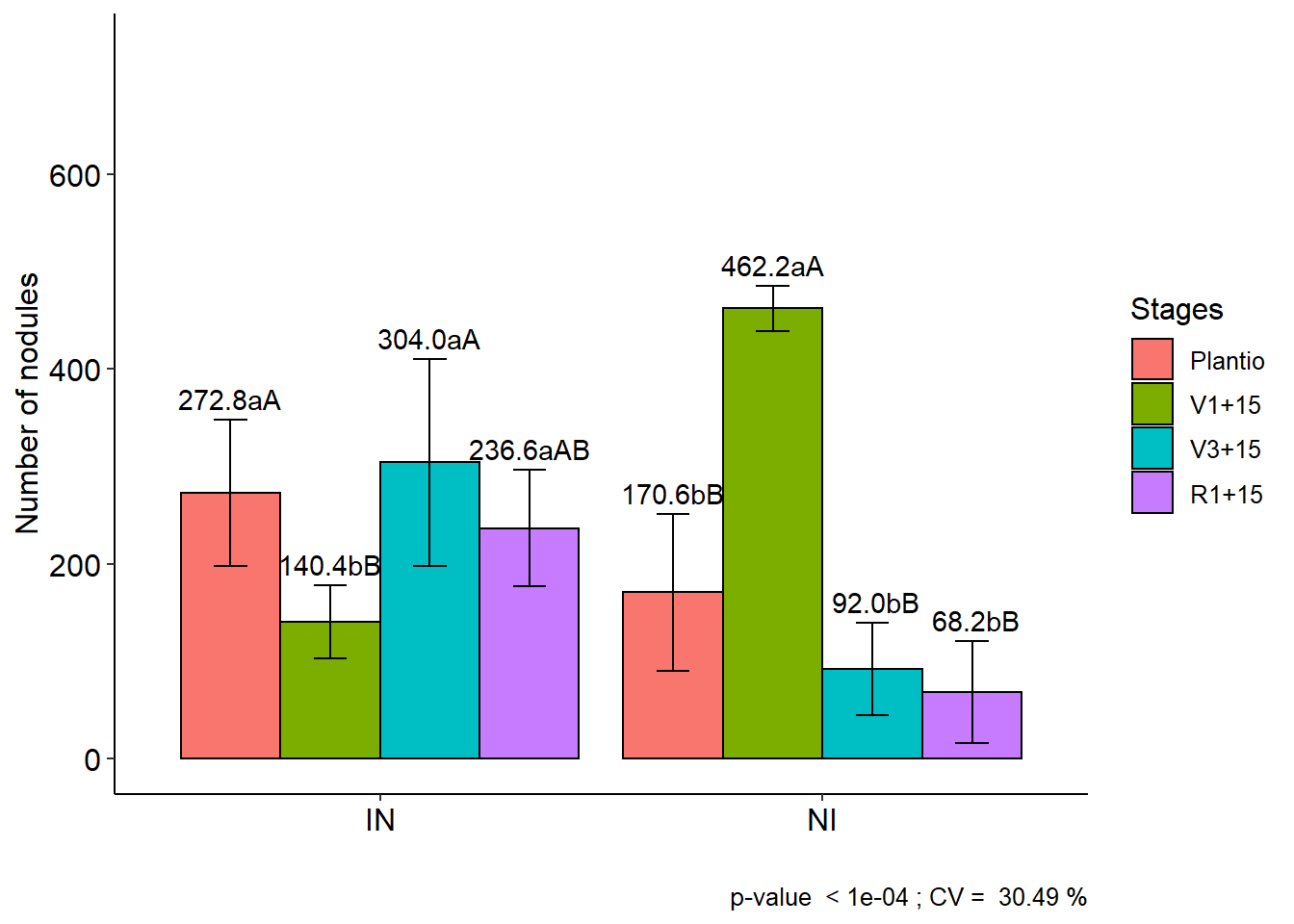
11.4 FAT2DIC.ad
data(cloro)
respAd=c(268, 322, 275, 350, 320)
with(cloro,FAT2DIC.ad(f1, f2, bloco, resp, respAd, ylab="Number of nodules", legend = "Stages"))##
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9680878 0.3125183## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 9.875441 0.1957427## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 2.092504 0.1892105## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 27.38
## Mean Factorial = 218.35
## Median Factorial = 185
## Mean Aditional = 307
## Median Aditional = 320
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## Fator1 1 16160.4 16160.400 4.140743 4.927778e-02
## Fator2 3 116554.5 38851.500 9.954833 6.428916e-05
## Fator1:Fator2 3 452096.2 150698.733 38.613199 2.411216e-11
## Ad x Factorial 1 34928.1 34928.100 8.949549 4.985733e-03
## Residuals 36 140500.0 3902.778## 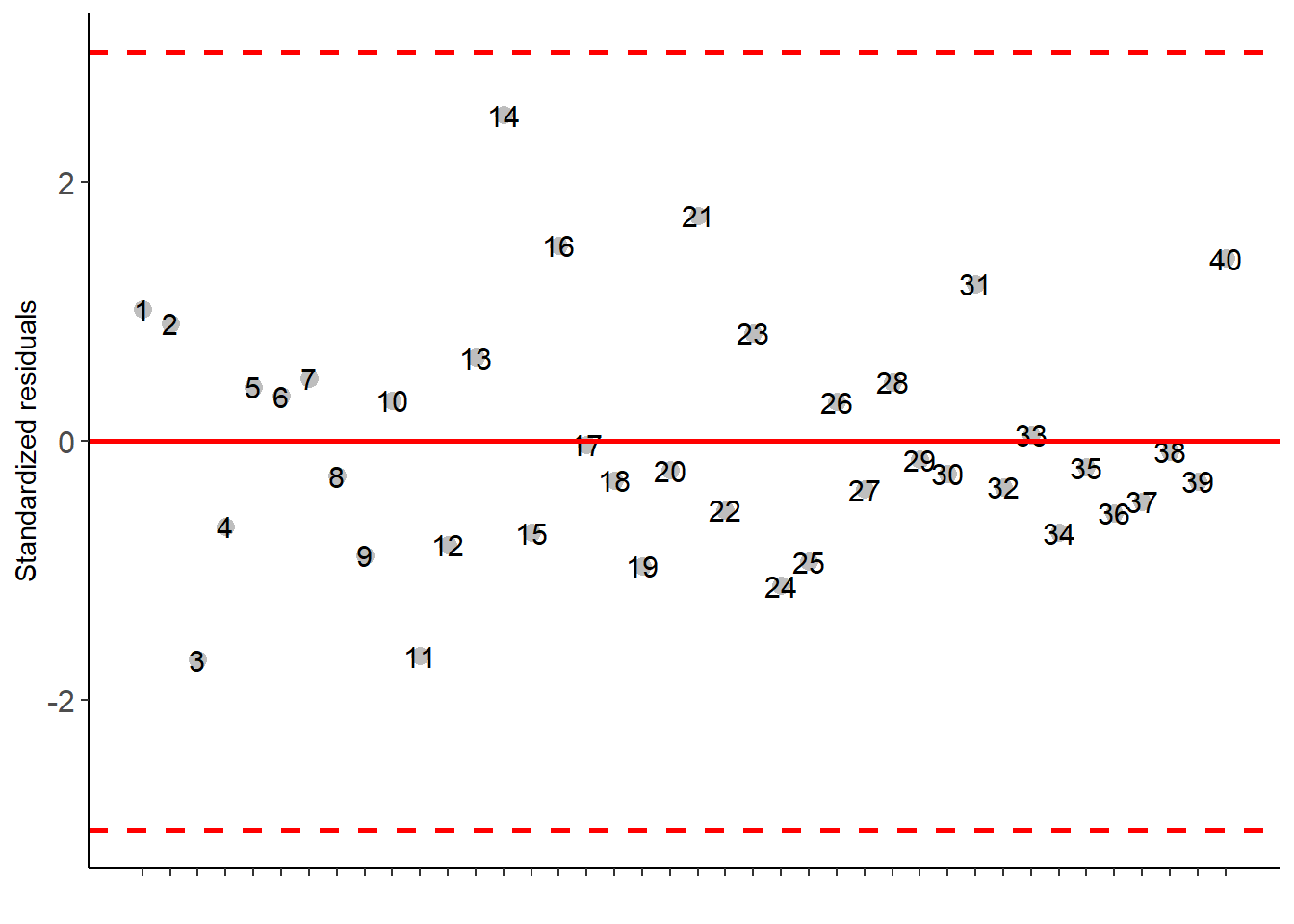
## -----------------------------------------------------------------
## Significant interaction: analyzing the interaction
## -----------------------------------------------------------------
## Df Sum Sq Mean Sq F value Pr(>F)
## Fator2 3 116555 38852 9.9548 6.429e-05 ***
## Fator2:Fator1 4 468257 117064 29.9951 5.126e-11 ***
## Fator2:Fator1: Plantio 1 26112 26112 6.6906 0.0138814 *
## Fator2:Fator1: V1+15 1 258888 258888 66.3343 1.101e-09 ***
## Fator2:Fator1: V3+15 1 112360 112360 28.7898 4.897e-06 ***
## Fator2:Fator1: R1+15 1 70896 70896 18.1656 0.0001393 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## -----------------------------------------------------------------
## Analyzing F2 inside of the level of F1
## -----------------------------------------------------------------
##
## Df Sum Sq Mean Sq F value Pr(>F)
## Fator1 1 16160 16160 4.1407 0.049278 *
## Fator1:Fator2 6 568651 94775 24.2840 2.774e-11 ***
## Fator1:Fator2: IN 3 75470 25157 6.4458 0.001317 **
## Fator1:Fator2: NI 3 493181 164394 42.1222 7.282e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## -----------------------------------------------------------------
## Final table
## -----------------------------------------------------------------
## Plantio V1+15 V3+15 R1+15
## IN 272.8 aA 140.4 bB 304.0 aA 236.6 aAB
## NI 170.6 bB 462.2 aA 92.0 bB 68.2 bB##
##
## Averages followed by the same lowercase letter in the column and
## uppercase in the row do not differ by the tukey (p< 0.05 )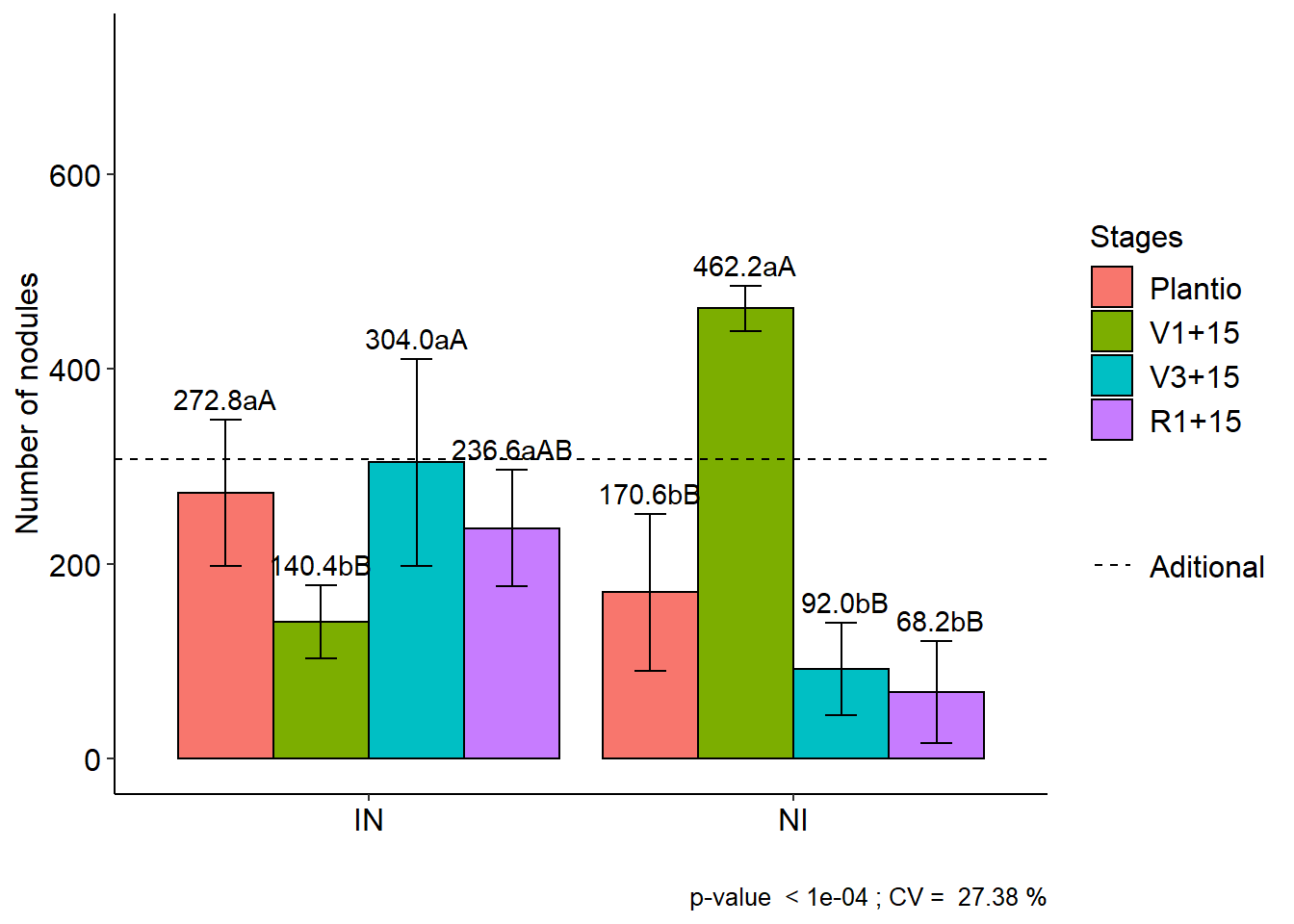
11.5 FAT2DBC.ad
data(cloro)
respAd=c(268, 322, 275, 350, 320)
with(cloro,
FAT2DBC.ad(f1, f2, bloco, resp, respAd, ylab="Number of nodules", legend = "Stages"))##
## -----------------------------------------------------------------
## Normality of errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Shapiro-Wilk normality test(W) 0.9548911 0.1117923## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal##
## -----------------------------------------------------------------
## Homogeneity of Variances
## -----------------------------------------------------------------
## Method Statistic p.value
## Bartlett test(Bartlett's K-squared) 16.11086 0.02412261## As the calculated p-value is less than the 5% significance level, H0 is rejected. Therefore, the variances are not homogeneous##
## -----------------------------------------------------------------
## Independence from errors
## -----------------------------------------------------------------
## Method Statistic p.value
## Durbin-Watson test(DW) 2.047899 0.1769663## As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent##
## -----------------------------------------------------------------
## Additional Information
## -----------------------------------------------------------------
##
## CV (%) = 27.38
## Mean Factorial = 218.35
## Median Factorial = 185
## Mean Aditional = 307
## Median Aditional = 320
## Possible outliers = No discrepant point
##
## -----------------------------------------------------------------
## Analysis of Variance
## -----------------------------------------------------------------
## Df Sum Sq Mean.Sq F value Pr(F)
## Fator1 1 16160.4 16160.400 4.1407431 4.927778e-02
## Fator2 3 116554.5 38851.500 9.9548327 6.428916e-05
## block 4 11613.6 2903.400 0.7439317 5.684322e-01
## Fator1:Fator2 3 452096.2 150698.733 38.6131986 2.411216e-11
## Ad x Factorial 1 475410.7 475410.700 121.8134178 4.174439e-13
## Residuals 36 140500.0 3902.778##
## Your analysis is not valid, suggests using a non-parametric test and try to transform the data## 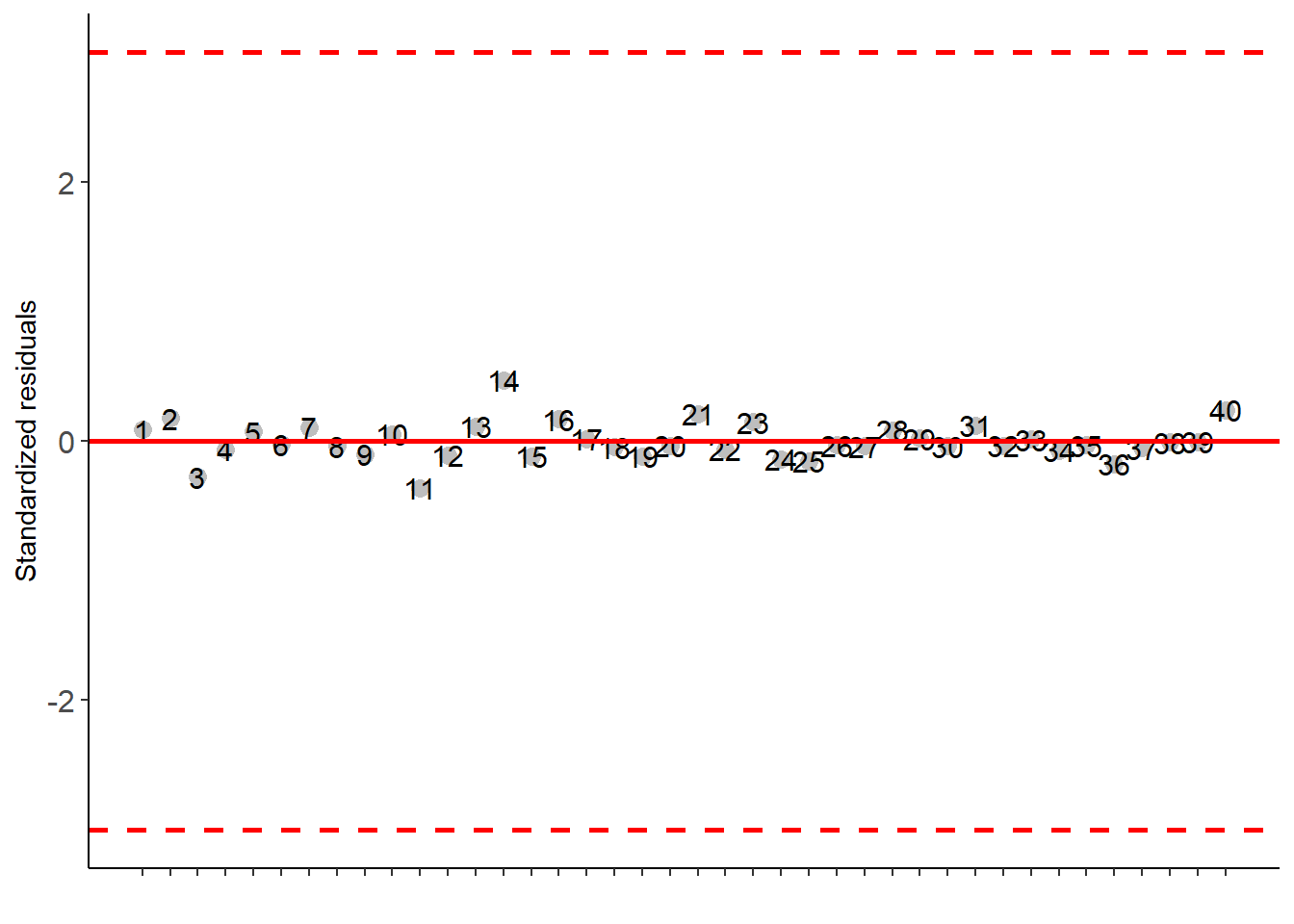
## -----------------------------------------------------------------
## Significant interaction: analyzing the interaction
## -----------------------------------------------------------------
## Df Sum Sq Mean Sq F value Pr(>F)
## Fator2 3 116555 38852 9.9548 6.429e-05 ***
## block 4 11614 2903 0.7439 0.5684322
## Fator2:Fator1 4 468257 117064 29.9951 5.126e-11 ***
## Fator2:Fator1: Plantio 1 26112 26112 6.6906 0.0138814 *
## Fator2:Fator1: V1+15 1 258888 258888 66.3343 1.101e-09 ***
## Fator2:Fator1: V3+15 1 112360 112360 28.7898 4.897e-06 ***
## Fator2:Fator1: R1+15 1 70896 70896 18.1656 0.0001393 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## -----------------------------------------------------------------
## Analyzing F2 inside of the level of F1
## -----------------------------------------------------------------
##
## Df Sum Sq Mean Sq F value Pr(>F)
## Fator1 1 16160 16160 4.1407 0.049278 *
## block 4 11614 2903 0.7439 0.568432
## Fator1:Fator2 6 568651 94775 24.2840 2.774e-11 ***
## Fator1:Fator2: IN 3 75470 25157 6.4458 0.001317 **
## Fator1:Fator2: NI 3 493181 164394 42.1222 7.282e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## -----------------------------------------------------------------
## Final table
## -----------------------------------------------------------------
## Plantio V1+15 V3+15 R1+15
## IN 272.8 aA 140.4 bB 304.0 aA 236.6 aAB
## NI 170.6 bB 462.2 aA 92.0 bB 68.2 bB##
##
## Averages followed by the same lowercase letter in the column and
## uppercase in the row do not differ by the tukey (p< 0.05 )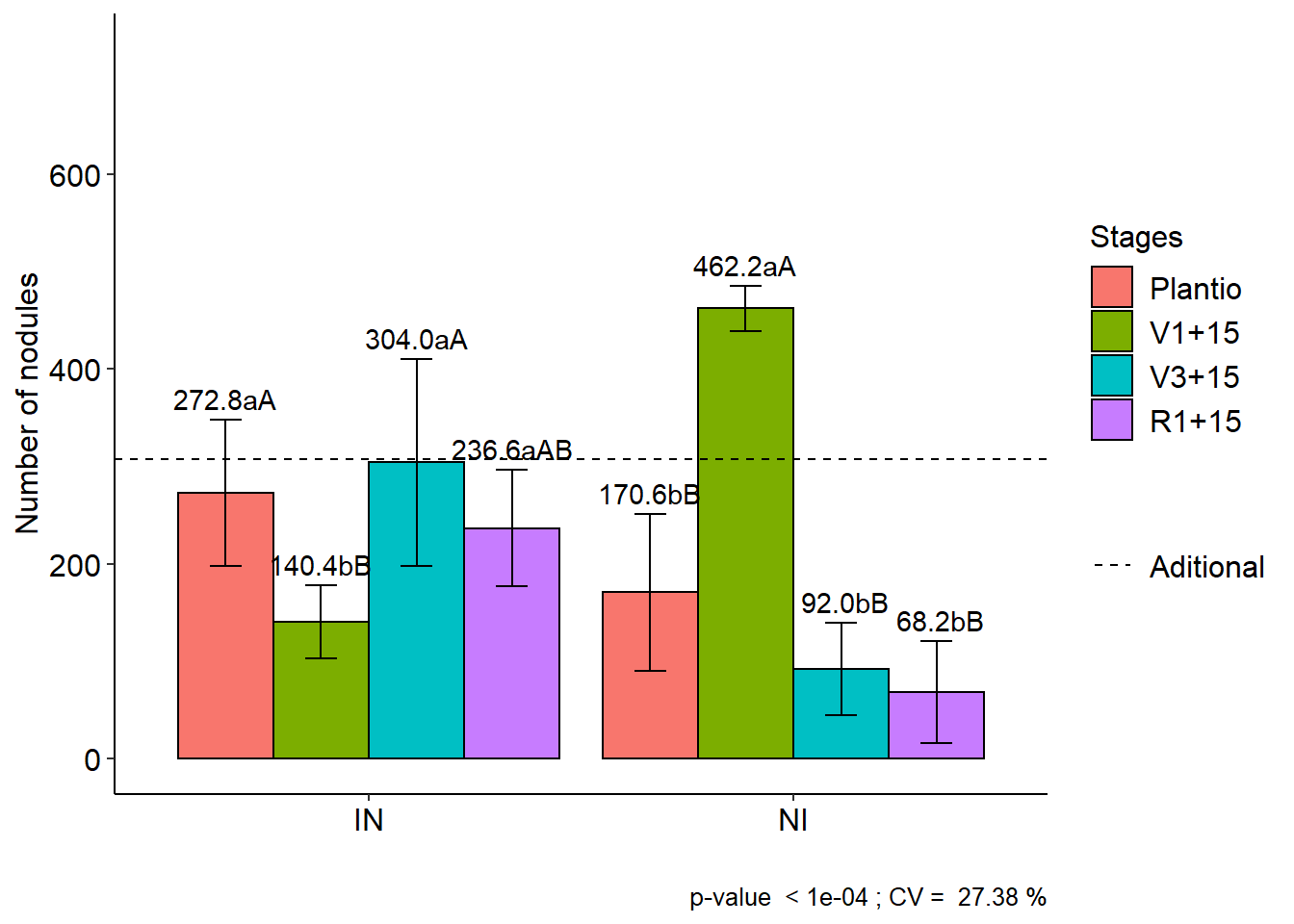
11.6 FAT2DIC.art
data(cloro)
with(cloro, FAT2DIC.art(f1,f2,resp))##
## -----------------------------------------------------------------
## Analysis of Variance of Aligned Rank Transformed Data
## -----------------------------------------------------------------
## FV Df Df.res SQ SQres Fvalue p-value
## fator1 fator1 1 32 640.0 4642.0 4.411891 4.365822e-02
## fator2 fator2 3 32 2570.2 2745.8 9.984510 8.493625e-05
## fator1:fator2 fator1:fator2 3 32 4103.8 1199.2 36.502557 1.916135e-10
##
##
## -----------------------------------------------------------------
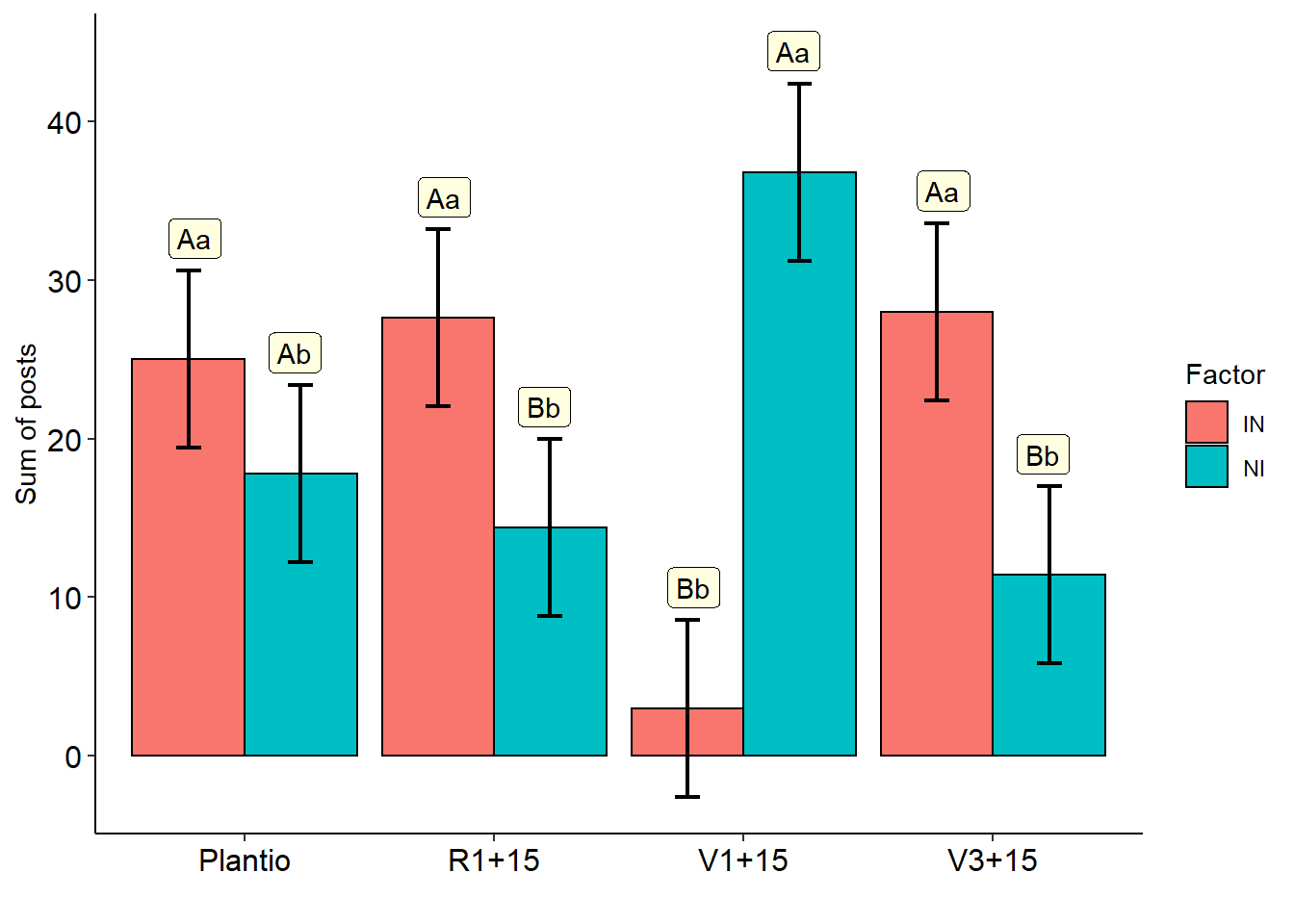
## fator1 fator2 emmean SE df lower.CL upper.CL .group
## 2 IN Plantio 25.0 2.7377 32 19.423488 30.576512 A
## 1 NI Plantio 17.8 2.7377 32 12.223488 23.376512 A
## 4 IN R1+15 27.6 2.7377 32 22.023488 33.176512 A
## 3 NI R1+15 14.4 2.7377 32 8.823488 19.976512 B
## 5 NI V1+15 36.8 2.7377 32 31.223488 42.376512 A
## 6 IN V1+15 3.0 2.7377 32 -2.576512 8.576512 B
## 8 IN V3+15 28.0 2.7377 32 22.423488 33.576512 A
## 7 NI V3+15 11.4 2.7377 32 5.823488 16.976512 B
##
##
## -----------------------------------------------------------------
## fator2 fator1 emmean SE df lower.CL upper.CL .group
## 3 V3+15 IN 28.0 2.7377 32 22.423488 33.576512 a
## 1 R1+15 IN 27.6 2.7377 32 22.023488 33.176512 a
## 2 Plantio IN 25.0 2.7377 32 19.423488 30.576512 a
## 4 V1+15 IN 3.0 2.7377 32 -2.576512 8.576512 b
## 8 V1+15 NI 36.8 2.7377 32 31.223488 42.376512 a
## 6 Plantio NI 17.8 2.7377 32 12.223488 23.376512 b
## 5 R1+15 NI 14.4 2.7377 32 8.823488 19.976512 b
## 7 V3+15 NI 11.4 2.7377 32 5.823488 16.976512 b## Warning in mean.default(mean): argumento não é numérico nem lógico: retornando
## NA## Warning: Removed 8 rows containing missing values (geom_label).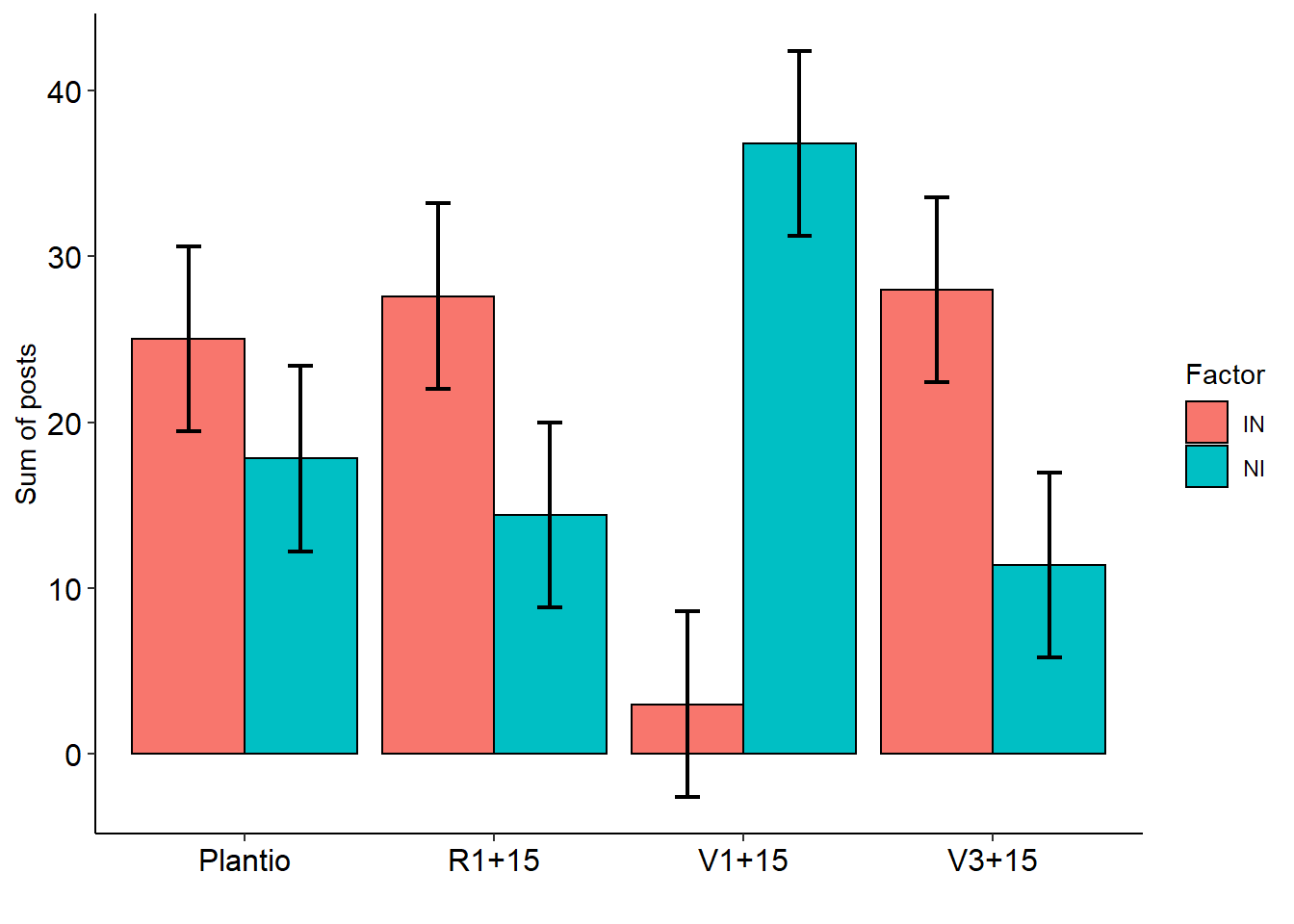
11.7 FAT2DBC.art
data(cloro)
with(cloro,FAT2DBC.art(f1,f2,bloco,resp))## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular##
## -----------------------------------------------------------------
## Analysis of Variance of Aligned Rank Transformed Data
## -----------------------------------------------------------------## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular## FV F Df Df.res p-value
## fator1 fator1 4.411891 1 28 4.482053e-02
## fator2 fator2 9.984510 3 28 1.212358e-04
## fator1:fator2 fator1:fator2 36.502557 3 28 8.217384e-10## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular
## boundary (singular) fit: see ?isSingular##
##
## -----------------------------------------------------------------
## fator1 fator2 emmean SE df lower.CL upper.CL .group
## 2 IN Plantio 25.0 2.7377 32 19.423488 30.576512 A
## 1 NI Plantio 17.8 2.7377 32 12.223488 23.376512 A
## 4 IN R1+15 27.6 2.7377 32 22.023488 33.176512 A
## 3 NI R1+15 14.4 2.7377 32 8.823488 19.976512 B
## 5 NI V1+15 36.8 2.7377 32 31.223488 42.376512 A
## 6 IN V1+15 3.0 2.7377 32 -2.576512 8.576512 B
## 8 IN V3+15 28.0 2.7377 32 22.423488 33.576512 A
## 7 NI V3+15 11.4 2.7377 32 5.823488 16.976512 B
##
##
## -----------------------------------------------------------------
## fator2 fator1 emmean SE df lower.CL upper.CL .group
## 3 V3+15 IN 28.0 2.7377 32 22.423488 33.576512 a
## 1 R1+15 IN 27.6 2.7377 32 22.023488 33.176512 a
## 2 Plantio IN 25.0 2.7377 32 19.423488 30.576512 a
## 4 V1+15 IN 3.0 2.7377 32 -2.576512 8.576512 b
## 8 V1+15 NI 36.8 2.7377 32 31.223488 42.376512 a
## 6 Plantio NI 17.8 2.7377 32 12.223488 23.376512 b
## 5 R1+15 NI 14.4 2.7377 32 8.823488 19.976512 b
## 7 V3+15 NI 11.4 2.7377 32 5.823488 16.976512 b