Analysis: Latin square design
DQL.RdThis is a function of the AgroR package for statistical analysis of experiments conducted in Latin Square and balanced design with a factor considering the fixed model.
DQL(
trat,
line,
column,
response,
norm = "sw",
homog = "bt",
alpha.f = 0.05,
alpha.t = 0.05,
quali = TRUE,
mcomp = "tukey",
grau = 1,
transf = 1,
constant = 0,
geom = "bar",
theme = theme_classic(),
sup = NA,
CV = TRUE,
ylab = "Response",
xlab = "",
textsize = 12,
labelsize = 4,
fill = "lightblue",
angle = 0,
family = "sans",
dec = 3,
width.column = NULL,
width.bar = 0.3,
addmean = TRUE,
errorbar = TRUE,
posi = "top",
point = "mean_sd",
angle.label = 0,
ylim = NA
)Arguments
- trat
Numerical or complex vector with treatments
- line
Numerical or complex vector with lines
- column
Numerical or complex vector with columns
- response
Numerical vector containing the response of the experiment.
- norm
Error normality test (default is Shapiro-Wilk)
- homog
Homogeneity test of variances (default is Bartlett)
- alpha.f
Level of significance of the F test (default is 0.05)
- alpha.t
Significance level of the multiple comparison test (default is 0.05)
- quali
Defines whether the factor is quantitative or qualitative (default is qualitative)
- mcomp
Multiple comparison test (Tukey (default), LSD, Scott-Knott and Duncan)
- grau
Degree of polynomial in case of quantitative factor (default is 1)
- transf
Applies data transformation (default is 1; for log consider 0; `angular` for angular transformation)
- constant
Add a constant for transformation (enter value)
- geom
Graph type (columns, boxes or segments)
- theme
ggplot2 theme (default is theme_classic())
- sup
Number of units above the standard deviation or average bar on the graph
- CV
Plotting the coefficient of variation and p-value of Anova (default is TRUE)
- ylab
Variable response name (Accepts the expression() function)
- xlab
Treatments name (Accepts the expression() function)
- textsize
Font size
- labelsize
Label size
- fill
Defines chart color (to generate different colors for different treatments, define fill = "trat")
- angle
x-axis scale text rotation
- family
Font family
- dec
Number of cells
- width.column
Width column if geom="bar"
- width.bar
Width errorbar
- addmean
Plot the average value on the graph (default is TRUE)
- errorbar
Plot the standard deviation bar on the graph (In the case of a segment and column graph) - default is TRUE
- posi
Legend position
- point
Defines whether to plot mean ("mean"), mean with standard deviation ("mean_sd" - default) or mean with standard error ("mean_se"). For parametric test it is possible to plot the square root of QMres (mean_qmres).
- angle.label
label angle
- ylim
Define a numerical sequence referring to the y scale. You can use a vector or the `seq` command.
Value
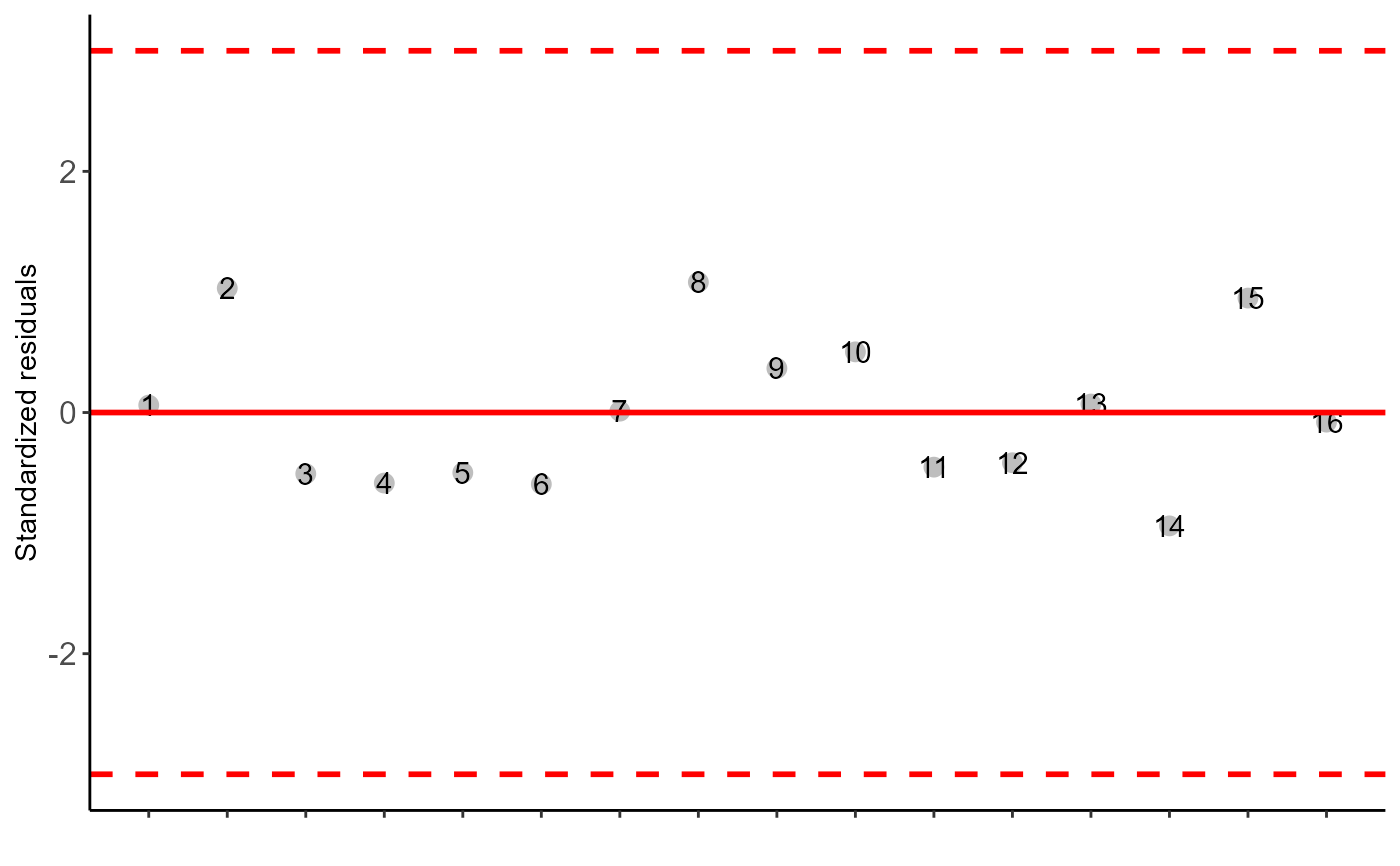
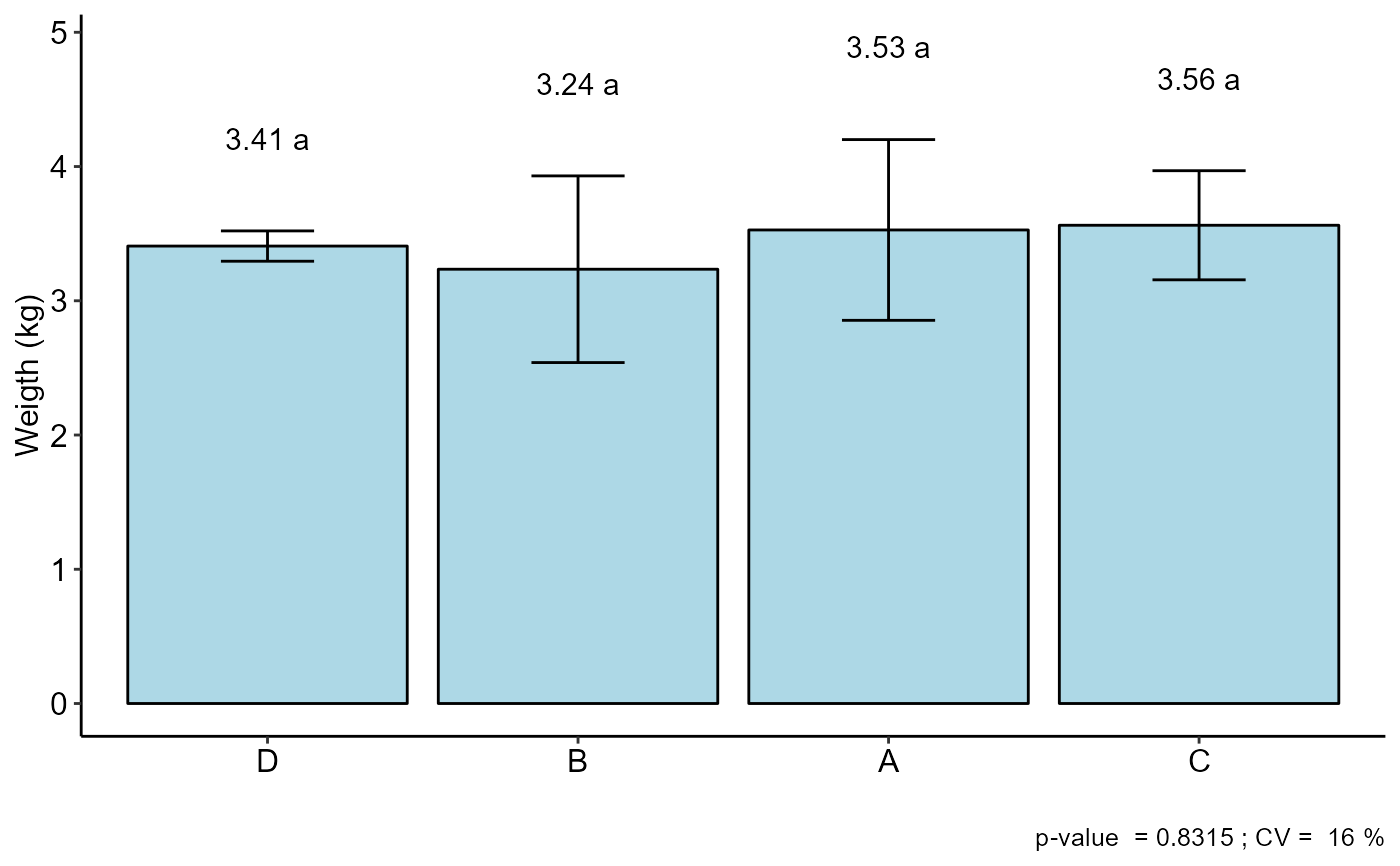
The table of analysis of variance, the test of normality of errors (Shapiro-Wilk ("sw"), Lilliefors ("li"), Anderson-Darling ("ad"), Cramer-von Mises ("cvm"), Pearson ("pearson") and Shapiro-Francia ("sf")), the test of homogeneity of variances (Bartlett ("bt") or Levene ("levene")), the test of independence of Durbin-Watson errors, the test of multiple comparisons (Tukey ("tukey"), LSD ("lsd"), Scott-Knott ("sk") or Duncan ("duncan")) or adjustment of regression models up to grade 3 polynomial, in the case of quantitative treatments. The column, segment or box chart for qualitative treatments is also returned. The function also returns a standardized residual plot.
Note
The ordering of the graph is according to the sequence in which the factor levels are arranged in the data sheet. The bars of the column and segment graphs are standard deviation.
CV and p-value of the graph indicate coefficient of variation and p-value of the F test of the analysis of variance.
In the final output when transformation (transf argument) is different from 1, the columns resp and respo in the mean test are returned, indicating transformed and non-transformed mean, respectively.
References
Principles and procedures of statistics a biometrical approach Steel, Torry and Dickey. Third Edition 1997
Multiple comparisons theory and methods. Departament of statistics the Ohio State University. USA, 1996. Jason C. Hsu. Chapman Hall/CRC.
Ramalho M.A.P., Ferreira D.F., Oliveira A.C. 2000. Experimentacao em Genetica e Melhoramento de Plantas. Editora UFLA.
Scott R.J., Knott M. 1974. A cluster analysis method for grouping mans in the analysis of variance. Biometrics, 30, 507-512.
Mendiburu, F., and de Mendiburu, M. F. (2019). Package ‘agricolae’. R Package, Version, 1-2.
Examples
library(AgroR)
data(porco)
with(porco, DQL(trat, linhas, colunas, resp, ylab="Weigth (kg)"))
#>
#> -----------------------------------------------------------------
#> Normality of errors (Shapiro-Wilk
#> -----------------------------------------------------------------
#> Method Statistic p.value
#> Shapiro-Wilk normality test(W) 0.9183353 0.1585848
#>
#> As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered normal
#>
#> -----------------------------------------------------------------
#> Homogeneity of Variances
#> -----------------------------------------------------------------
#> Method Statistic p.value
#> Bartlett test(Bartlett's K-squared) 1.207666 0.7511662
#>
#> As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, the variances can be considered homogeneous
#>
#> -----------------------------------------------------------------
#> Independence from errors
#> -----------------------------------------------------------------
#> Method Statistic p.value
#> Durbin-Watson test(DW) 2.028993 0.2932159
#>
#> As the calculated p-value is greater than the 5% significance level, hypothesis H0 is not rejected. Therefore, errors can be considered independent
#>
#> -----------------------------------------------------------------
#> Additional Information
#> -----------------------------------------------------------------
#>
#> CV (%) = 16
#> MStrat/MST = 0.1
#> Mean = 3.4331
#> Median = 3.39
#> Possible outliers = No discrepant point
#>
#> -----------------------------------------------------------------
#> Analysis of Variance
#> -----------------------------------------------------------------
#> Df Sum Sq Mean.Sq F value Pr(F)
#> trat 3 0.2622187 0.08740625 0.2898586 0.8315413
#> line 3 0.1065687 0.03552292 0.1178019 0.9463594
#> column 3 1.4274687 0.47582292 1.5779347 0.2899683
#> Residuals 6 1.8092875 0.30154792
#>
#> As the calculated p-value is greater than the 5% significance level, H0 is not rejected
#>
#> -----------------------------------------------------------------
#> Multiple Comparison Test: Tukey HSD
#> -----------------------------------------------------------------
#> [1] "H0 is not rejected"
#>
#>