Analysis: Linear regression graph

Linear regression analysis of an experiment with a quantitative factor or isolated effect of a quantitative factor

polynomial(
  trat,
  resp,
  ylab = "Response",
  xlab = "Independent",
  yname.poly = "y",
  xname.poly = "x",
  grau = NA,
  theme = theme_classic(),
  point = "mean_sd",
  color = "gray80",
  posi = "top",
  textsize = 12,
  se = FALSE,
  ylim = NA,
  family = "sans",
  pointsize = 4.5,
  linesize = 0.8,
  width.bar = NA,
  n = NA,
  SSq = NA,
  DFres = NA
)

Arguments

trat

Numerical vector with treatments (Declare as numeric)

resp

Numerical vector containing the response of the experiment.

ylab

Dependent variable name (Accepts the expression() function)

xlab

Independent variable name (Accepts the expression() function)

yname.poly

Y name in equation

xname.poly

X name in equation

grau

Degree of the polynomial (1, 2 or 3)

theme

ggplot2 theme (default is theme_classic())

point

Defines whether to plot mean ("mean"), all repetitions ("all"),mean with standard deviation ("mean_sd") or mean with standard error (default - "mean_se").

color

Graph color (default is gray80)

posi

Legend position

textsize

Font size

se

Adds confidence interval (default is FALSE)

ylim

y-axis scale

family

Font family

pointsize

Point size

linesize

line size (Trendline and Error Bar)

width.bar

width of the error bars of a regression graph.

n

Number of decimal places for regression equations

SSq

Sum of squares of the residue

DFres

Residue freedom degrees

Value

Returns linear, quadratic or cubic regression analysis.

See also

polynomial2, polynomial2_color

Author

Gabriel Danilo Shimizu, shimizu@uel.br

Leandro Simoes Azeredo Goncalves

Rodrigo Yudi Palhaci Marubayashi

Examples

data("phao")
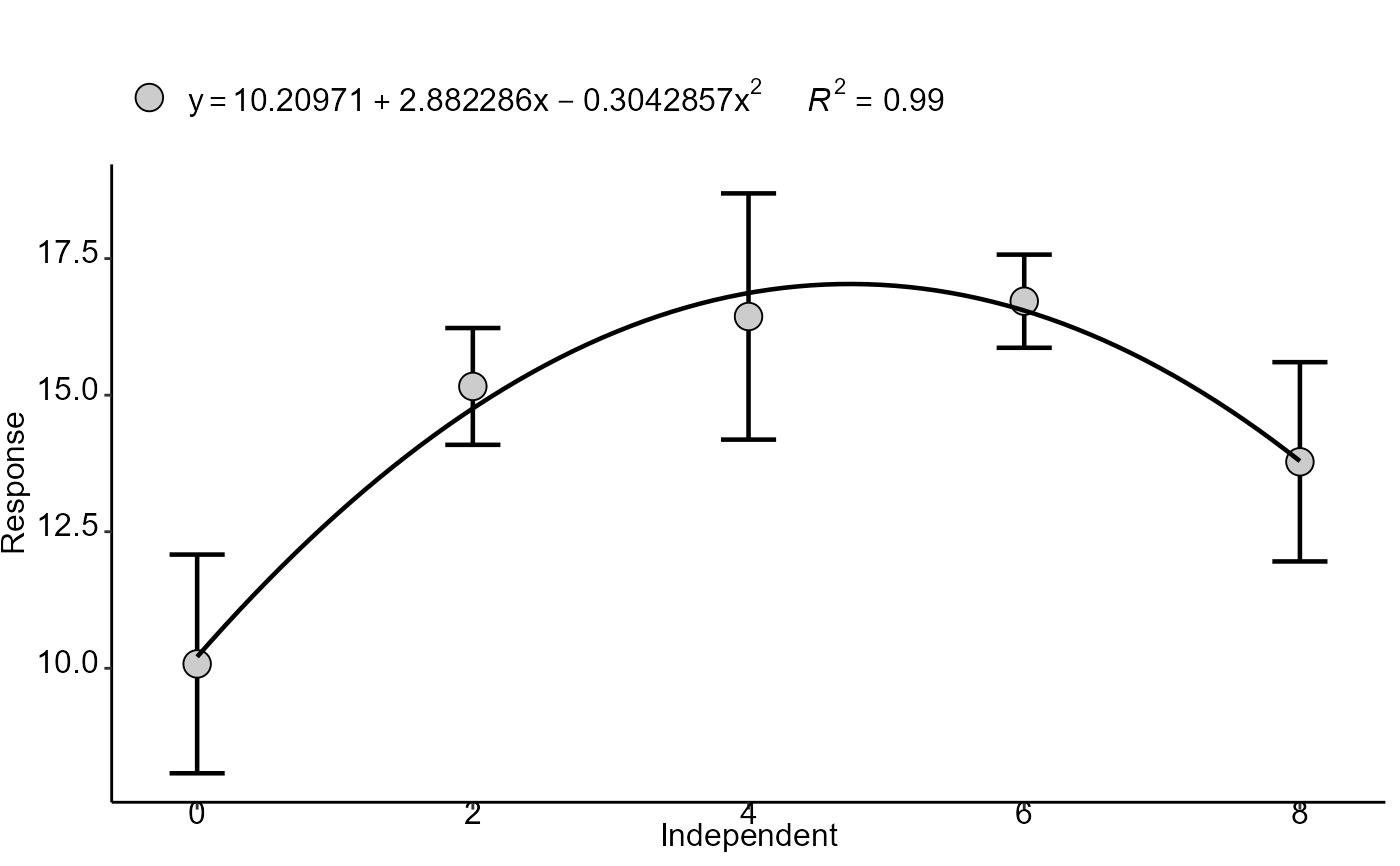
with(phao, polynomial(dose,comp, grau = 2))
#> 
#> ----------------------------------------------------
#> Regression Models
#> ----------------------------------------------------
#>               Estimate Std. Error   t value     Pr(>|t|)
#> (Intercept) 10.2097143 0.68981140 14.800733 6.427099e-13
#> trat         2.8822857 0.40856781  7.054608 4.456995e-07
#> I(trat^2)   -0.3042857 0.04897332 -6.213296 2.971498e-06
#> 
#> ----------------------------------------------------
#> Deviations from regression
#> ----------------------------------------------------
#>           Df        SSq         MSQ          F      p-value
#> Linear     1  40.140800  40.1408000 14.0529338 1.265122e-03
#> Quadratic  1 103.700571 103.7005714 36.3046392 6.852202e-06
#> Deviation  2   1.968229   0.9841143  0.3445296 7.126767e-01
#> Residual  20  57.128000   2.8564000                        
#> [[1]]

#>