Analysis: Logistic regression
logistic.RdLogistic regression is a very popular analysis in agrarian sciences, such as in fruit growth curves, seed germination, etc...The logistic function performs the analysis using 3 or 4 parameters of the logistic model, being imported from the LL function .3 or LL.4 of the drc package (Ritz & Ritz, 2016).
logistic(
trat,
resp,
npar = "LL.3",
error = "SE",
ylab = "Dependent",
xlab = expression("Independent"),
theme = theme_classic(),
legend.position = "top",
r2 = "all",
width.bar = NA,
scale = "none",
textsize = 12,
font.family = "sans"
)Arguments
- trat
Numerical or complex vector with treatments
- resp
Numerical vector containing the response of the experiment.
- npar
Number of model parameters
- error
Error bar (It can be SE - default, SD or FALSE)
- ylab
Variable response name (Accepts the expression() function)
- xlab
Treatments name (Accepts the expression() function)
- theme
ggplot2 theme (default is theme_bw())
- legend.position
Legend position (default is c(0.3,0.8))
- r2
Coefficient of determination of the mean or all values (default is all)
- width.bar
Bar width
- scale
Sets x scale (default is none, can be "log")
- textsize
Font size
- font.family
Font family (default is sans)
Value
The function allows the automatic graph and equation construction of the logistic model, provides important statistics, such as the Akaike (AIC) and Bayesian (BIC) inference criteria, coefficient of determination (r2), square root of the mean error ( RMSE).
Details
The three-parameter log-logistic function with lower limit 0 is $$f(x) = 0 + \frac{d}{1+\exp(b(\log(x)-\log(e)))}$$ The four-parameter log-logistic function is given by the expression $$f(x) = c + \frac{d-c}{1+\exp(b(\log(x)-\log(e)))}$$ The function is symmetric about the inflection point (e).
References
Seber, G. A. F. and Wild, C. J (1989) Nonlinear Regression, New York: Wiley and Sons (p. 330).
Ritz, C.; Strebig, J.C.; Ritz, M.C. Package ‘drc’. Creative Commons: Mountain View, CA, USA, 2016.
Examples
data("emerg")
with(emerg, logistic(time, resp,xlab="Time (days)",ylab="Emergence (%)"))
#> $Coefficients
#> Estimate Std Error t value P-value
#> b:(Intercept) -21.61550 3.56104842 -6.069982 8.912223e-08 **
#> d:(Intercept) 81.08478 1.73973123 46.607646 1.052258e-49 **
#> e:(Intercept) 10.01534 0.08344181 120.027785 1.852496e-74 **
#>
#> $values
#> Parameter values
#> 1 AIC 434.790623
#> 2 BIC 443.426156
#> 3 r-squared 0.960000
#> 4 RMSE 6.789404
#>
#> $graph
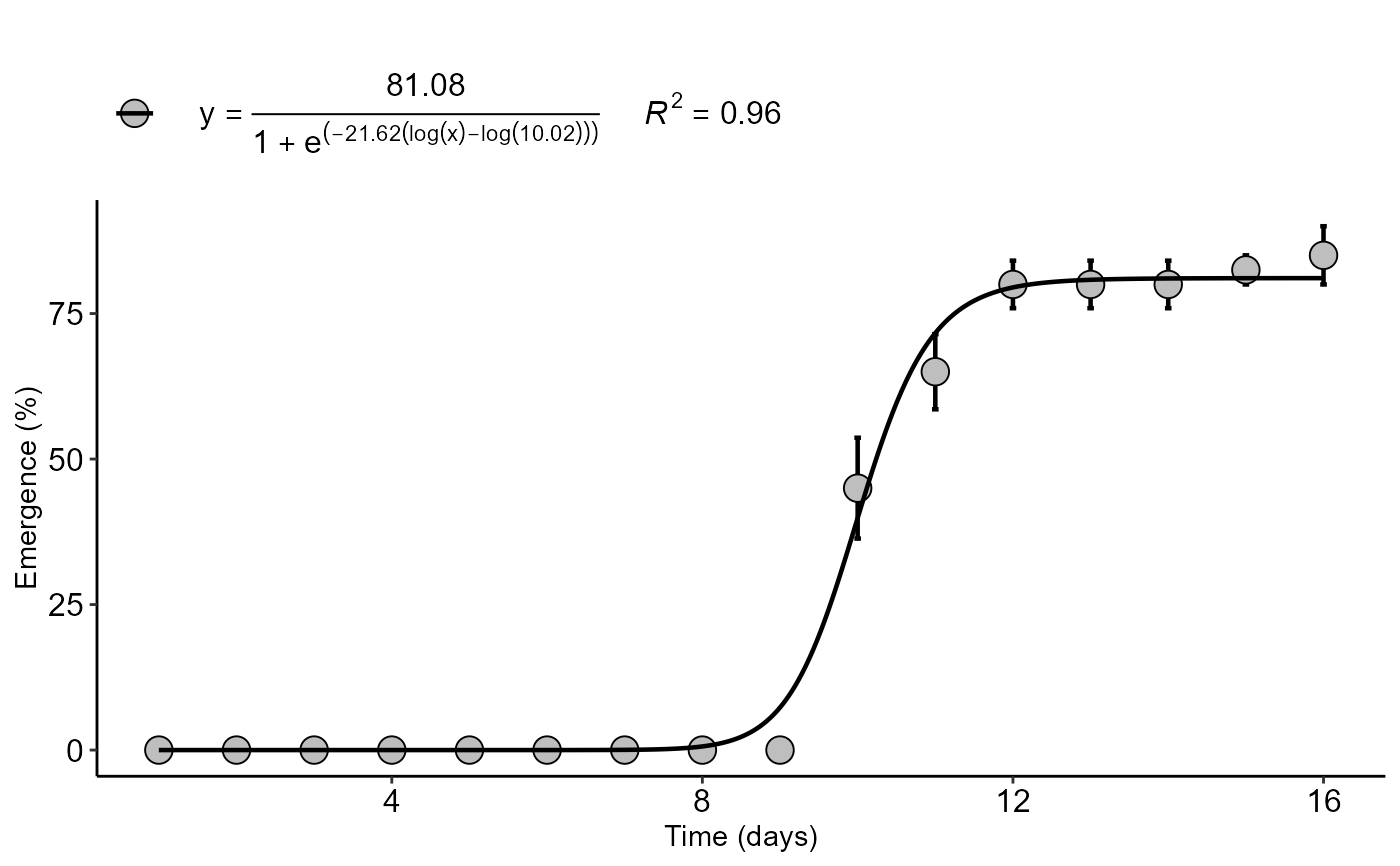 #>
with(emerg, logistic(time, resp,npar="LL.4",xlab="Time (days)",ylab="Emergence (%)"))
#> $Coefficients
#> Estimate Std Error t value P-value
#> b:(Intercept) -21.32060 3.53758836 -6.0268741 1.107976e-07 **
#> c:(Intercept) -0.66355 1.22035166 -0.5437367 5.886374e-01 ns
#> d:(Intercept) 81.13072 1.75277913 46.2869040 5.929524e-49 **
#> e:(Intercept) 10.00733 0.08446958 118.4725590 3.826623e-73 **
#>
#> $values
#> Parameter values
#> 1 AIC 436.475255
#> 2 BIC 447.269671
#> 3 r-squared 0.960000
#> 4 RMSE 6.772697
#>
#> $graph
#>
with(emerg, logistic(time, resp,npar="LL.4",xlab="Time (days)",ylab="Emergence (%)"))
#> $Coefficients
#> Estimate Std Error t value P-value
#> b:(Intercept) -21.32060 3.53758836 -6.0268741 1.107976e-07 **
#> c:(Intercept) -0.66355 1.22035166 -0.5437367 5.886374e-01 ns
#> d:(Intercept) 81.13072 1.75277913 46.2869040 5.929524e-49 **
#> e:(Intercept) 10.00733 0.08446958 118.4725590 3.826623e-73 **
#>
#> $values
#> Parameter values
#> 1 AIC 436.475255
#> 2 BIC 447.269671
#> 3 r-squared 0.960000
#> 4 RMSE 6.772697
#>
#> $graph
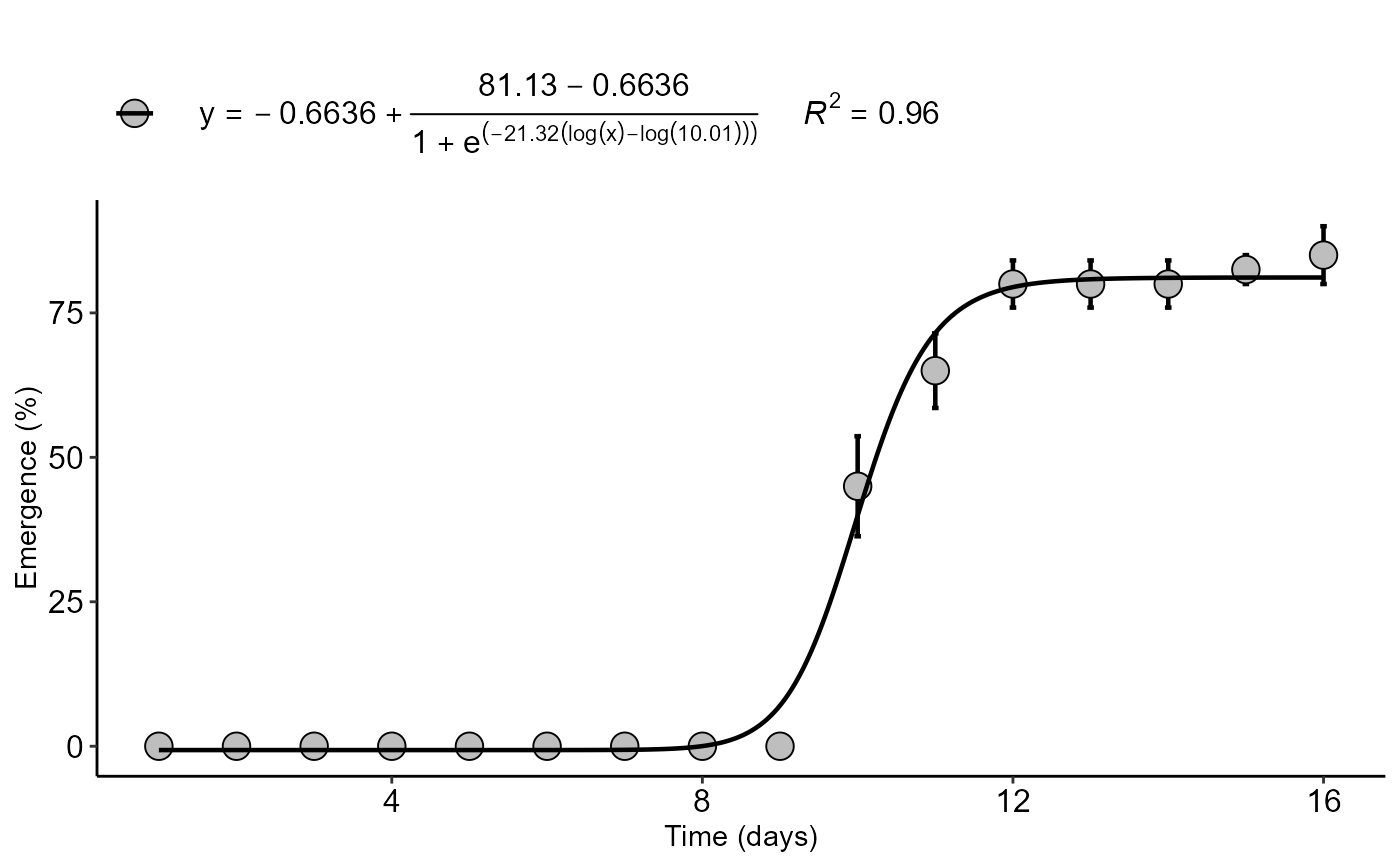 #>
#>