Analysis: Linear regression graph in double factorial with color graph
polynomial2_color.RdLinear regression analysis for significant interaction of an experiment with two factors, one quantitative and one qualitative
polynomial2_color(
fator1,
resp,
fator2,
color = NA,
grau = NA,
ylab = "Response",
xlab = "independent",
theme = theme_classic(),
se = FALSE,
point = "mean_se",
legend.title = "Tratamentos",
posi = "top",
textsize = 12,
ylim = NA,
family = "sans",
width.bar = NA,
pointsize = 5,
linesize = 0.8,
separate = c("(\"", "\")"),
n = NA,
DFres = NA,
SSq = NA
)Arguments
- fator1
Numeric or complex vector with factor 1 levels
- resp
Numerical vector containing the response of the experiment.
- fator2
Numeric or complex vector with factor 2 levels
- color
Graph color (default is NA)
- grau
Degree of the polynomial (1,2 or 3)
- ylab
Dependent variable name (Accepts the expression() function)
- xlab
Independent variable name (Accepts the expression() function)
- theme
ggplot2 theme (default is theme_classic())
- se
Adds confidence interval (default is FALSE)
- point
Defines whether to plot all points ("all"), mean ("mean"), mean with standard deviation ("mean_sd") or mean with standard error (default - "mean_se").
- legend.title
Title legend
- posi
Legend position
- textsize
Font size (default is 12)
- ylim
y-axis scale
- family
Font family (default is sans)
- width.bar
width of the error bars of a regression graph.
- pointsize
Point size (default is 4)
- linesize
line size (Trendline and Error Bar)
- separate
Separation between treatment and equation (default is c("(\"","\")"))
- n
Number of decimal places for regression equations
- DFres
Residue freedom degrees
- SSq
Sum of squares of the residue
Value
Returns two or more linear, quadratic or cubic regression analyzes.
See also
Examples
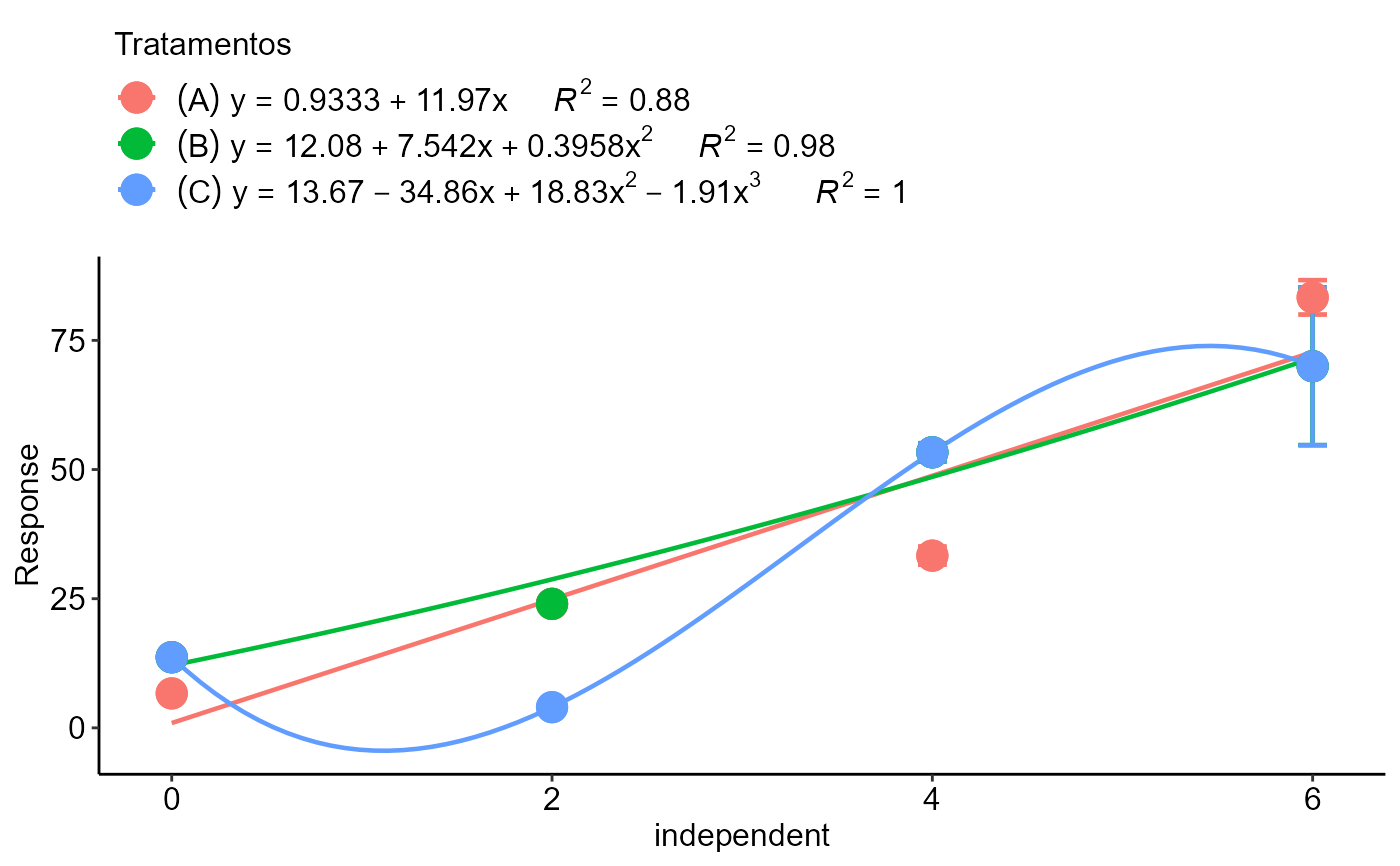
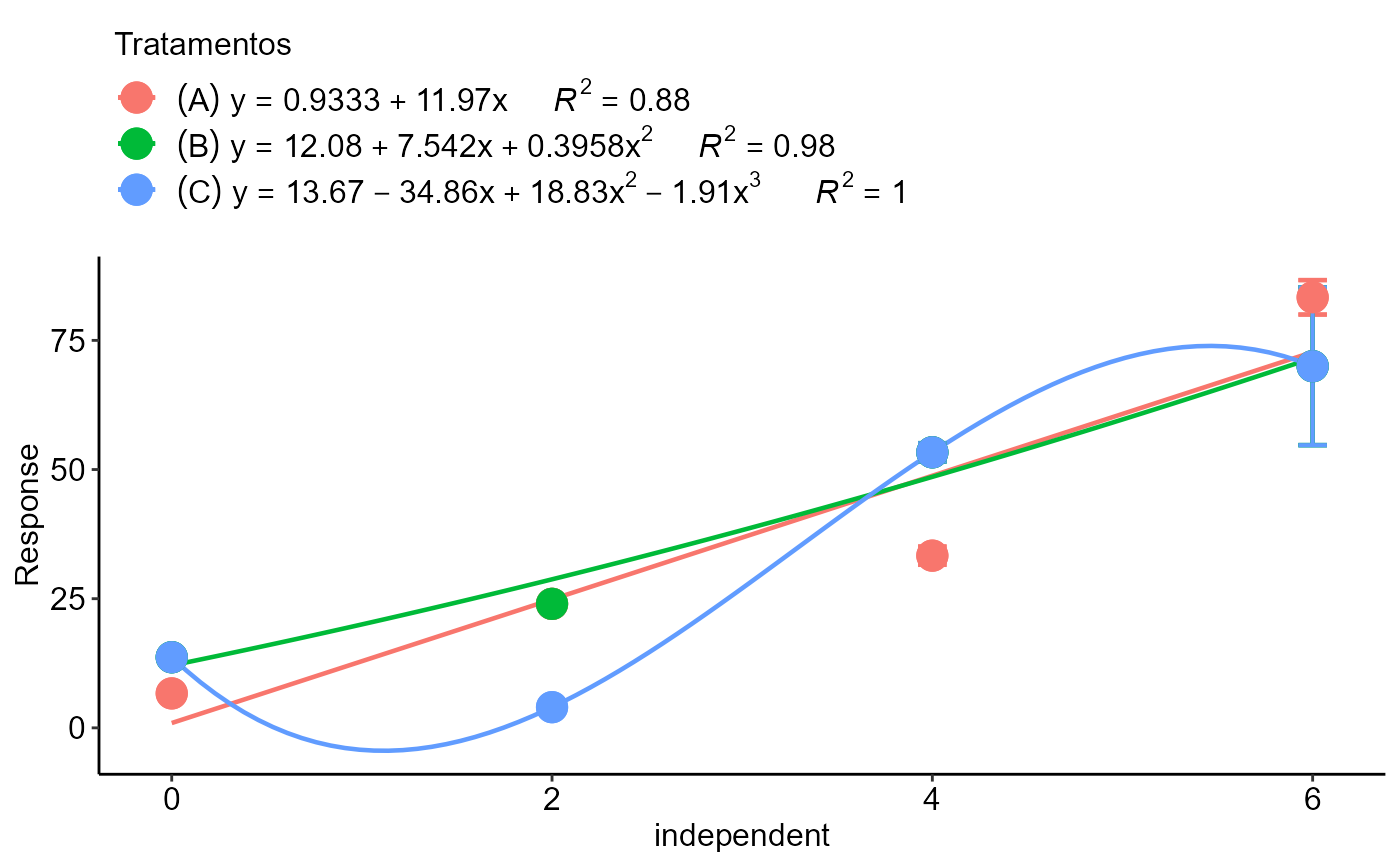
dose=rep(c(0,0,0,2,2,2,4,4,4,6,6,6),3)
resp=c(8,7,5,23,24,25,30,34,36,80,90,80,
12,14,15,23,24,25,50,54,56,80,90,40,
12,14,15,3,4,5,50,54,56,80,90,40)
trat=rep(c("A","B","C"),e=12)
polynomial2_color(dose, resp, trat, grau=c(1,2,3))
#> Warning: NaNs produced
#>
#> ----------------------------------------------------
#> Regression Models
#> ----------------------------------------------------
#> $A
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.9333333 5.395430 0.1729859 8.661137e-01
#> x 11.9666667 1.441989 8.2987205 8.528803e-06
#>
#> $B
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 12.0833333 7.4460094 1.6227932 0.1390822
#> x 7.5416667 5.9788110 1.2613991 0.2388777
#> I(x^2) 0.3958333 0.9549306 0.4145153 0.6882023
#>
#> $C
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 13.666667 7.7064187 1.773413 0.11409087
#> x -34.861111 14.7845901 -2.357936 0.04610656
#> I(x^2) 18.833333 6.5334343 2.882609 0.02042957
#> I(x^3) -1.909722 0.7180032 -2.659769 0.02881582
#>
#>
#> ----------------------------------------------------
#> Anova
#> ----------------------------------------------------
#> $`Anova A`
#> Df SSq MSQ F p-value
#> Linear 1 8592.067 8592.0667 70.07576 1.401237e-08
#> Deviation 2 1155.600 577.8000 4.71246 1.877977e-02
#> Residual 24 2942.667 122.6111
#>
#> $`Anova B`
#> Df SSq MSQ F p-value
#> Linear 1 5900.41667 5900.41667 48.1230177 3.571320e-07
#> Quadratic 1 30.08333 30.08333 0.2453557 6.248694e-01
#> Deviation 1 150.41667 150.41667 1.2267784 2.790120e-01
#> Residual 24 2942.66667 122.61111
#>
#> $`Anova C`
#> Df SSq MSQ F p-value
#> Linear 1 7.150417e+03 7150.4167 58.317852 7.114165e-08
#> Quadratic 1 5.200833e+02 520.0833 4.241731 5.044762e-02
#> Cubic 1 1.260417e+03 1260.4167 10.279792 3.783350e-03
#> Deviation 0 4.547474e-13 -Inf -Inf NaN
#> Residual 24 2.942667e+03 122.6111
#>